백준 27725번 지수를 더하자

🔒문제 url

https://www.acmicpc.net/problem/27725

🔑알고리즘

우선 문제부터 이해해보자.
$i = 10$이고, $P = \{2,3\}$인 경우를 예로 들어 생각하면 아래와 같다.

$i = 1$일 때, $\frac{1}{2^{a^1} \times 3^{a^2}}$가 양의 정수를 만족하는 $a^1+ a^2$의 최댓값은 0 + 0 = 0 이다.

$i = 2$일 때, $\frac{2}{2^{a^1} \times 3^{a^2}}$가 양의 정수를 만족하는 $a^1+ a^2$의 최댓값은 1 + 0 = 1 이다.

$i = 3$일 때, $\frac{3}{2^{a^1} \times 3^{a^2}}$가 양의 정수를 만족하는 $a^1+ a^2$의 최댓값은 0 + 1 = 1 이다.

$i = 4$일 때, $\frac{4}{2^{a^1} \times 3^{a^2}}$가 양의 정수를 만족하는 $a^1+ a^2$의 최댓값은 2 + 0 = 2 이다.

$i = 5$일 때, $\frac{5}{2^{a^1} \times 3^{a^2}}$가 양의 정수를 만족하는 $a^1+ a^2$의 최댓값은 0 + 0 = 0 이다.

$i = 6$일 때, $\frac{6}{2^{a^1} \times 3^{a^2}}$가 양의 정수를 만족하는 $a^1+ a^2$의 최댓값은 1 + 1 = 2 이다.

$i = 7$일 때, $\frac{7}{2^{a^1} \times 3^{a^2}}$가 양의 정수를 만족하는 $a^1+ a^2$의 최댓값은 0 + 0 = 0 이다.

$i = 8$일 때, $\frac{8}{2^{a^1} \times 3^{a^2}}$가 양의 정수를 만족하는 $a^1+ a^2$의 최댓값은 3 + 0 = 3 이다.

$i = 9$일 때, $\frac{9}{2^{a^1} \times 3^{a^2}}$가 양의 정수를 만족하는 $a^1+ a^2$의 최댓값은 0 + 2 = 2 이다.

$i = 10$일 때, $\frac{10}{2^{a^1} \times 3^{a^2}}$가 양의 정수를 만족하는 $a^1+ a^2$의 최댓값은 1 + 0 = 1 이다.

따라서 최댓값의 합인 $b_i = 1 + 1 + 2 + 2 + 3 + 2 + 1 = 12$가 되어야 한다.

$p1 = 2$부터 생각해보자.
$2$로 나누어 떨어지는 $i$는 $2, 4, 6, 8, 10$이다.
$2^2$로 나누어 떨어지는 $i$는 $4, 8$이 되고,

이는 $2$로 나누어 떨어지는 수를 $2$로 한 번 더 나눌 수 있는 수와 같다.

위에 근거하여 표를 작성하면 아래와 같다.

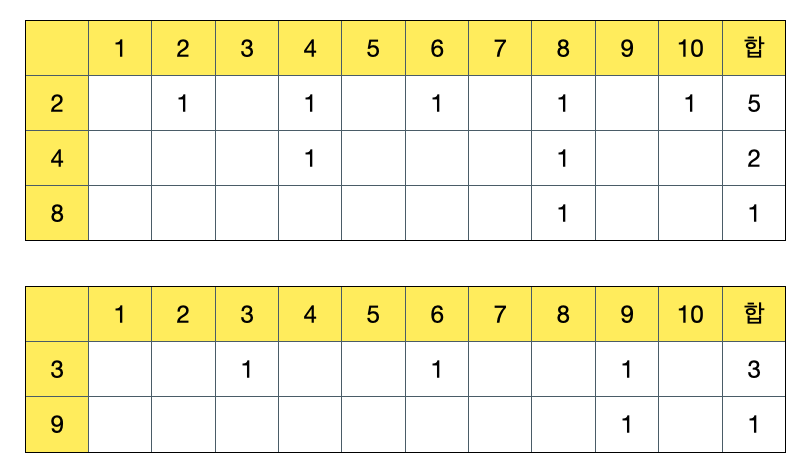
즉, 각 가능한 모든 소인수에 대하여 나누어 떨어지는 수의 합이 출력 답안이 된다.

🐾부분 코드

void solution()
{
    ll ans = 0;
    for (auto p : prime)
    {
        ll temp = p;
        while (p <= k)
        {
            ans += k / p;
            p *= temp;
        }
    }
    cout << ans;
}

모든 소인수에 대하여, 해당 소인수로 나누어 떨어지는 $i$의 갯수를 구하여 ans에 더한 뒤 출력한다.

🪄전체 코드

#include <bits/stdc++.h>

using namespace std;
#define IAMFAST ios_base::sync_with_stdio(false);cin.tie(0);
typedef long long ll;

ll n, k;
vector<ll> prime;

void INPUT()
{
    IAMFAST
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        ll p;
        cin >> p;
        prime.emplace_back(p);
    }
    cin >> k;
}

void solution()
{
    ll ans = 0;
    for (auto p : prime)
    {
        ll temp = p;
        while (p <= k)
        {
            ans += k / p;
            p *= temp;
        }
    }
    cout << ans;
}

int main()
{
    INPUT();
    solution();
}

🥇문제 후기