---

03-02 기초 수학 문제풀이

---

31_약수와 소수

# 100부터 1000사이의 난수에 대해서 약수, 소수 그리고 소인수를 출력하는 프로그램을 만들어보자
# 약수: 나누어 떨어지는 수
# 소수: 1외에 약수가 자기 자신뿐인 수
# 소인수: 약수(인수)이면서 소수인 수

import random

rNum = random.randint(100, 1000)
print(f'rNum: {rNum}')

for num in range(1, rNum+1):
    
    soinsuFlag = 0 # 소인수 계산용
    
    # 약수
    if rNum % num == 0:
        print(f'[약수]: {num}')
        soinsuFlag += 1 # 약수이면서 소수인 것 찾기용
        
    # 소수
    if num != 1: # 1은 합성수도 아니고, 수수도 아니기 때문에
        flag = True
        for n in range(2, num):
            if num % n == 0: # 그럼 약수가 있다는 뜻이니, 소수인 조건에 뒤배되니
                flag = False # False로 바꾸고 반복문을 빠져나오게 한다
                break
        if flag: #위 반복문에서 약수가 없었다면, 그 수는 소수일 수 있겠다
            print(f'[소수]: {num}')
            soinsuFlag += 1 # 약수이면서 소수인 것 찾기용
    
    # 소인수(약수이면서 소수인 수)
    if soinsuFlag >= 2: # soinsuFlag가 2보다 크거가 같으면 num은 소인수라고 판단하겠다
        print(f'[소인수]:{num}')

---

32_소인수와 소인수분해

# 100부터 1000사이의 난수를 소인수분해를 하고 각각의 소인수에 대한 지수를 출력하는 프로그램을 만들어보자
# 소인수분해란 어떤 수를 소인수의 곲으로 나타낸 것
# 2 x x 5 = 2^2 * 5^1 --> 여기서 2, 5를 '밑'이라 하고, ^2, ^1의 숫자를 '지수'라 한다 
import random

rNum = random.randint(100, 1000)
print(f'rNum: {rNum}')

soinList = [] # 이 배열에다 찾은 소인수를 넣을 것이다
n = 2

# 소인수 구하기
while n <= rNum:
    if rNum % n == 0: # 소인수분해가 하나 된 것
        print(f'소인수: {n}')
        soinList.append(n) # 빈 리스트에 소인수 하나씩 추가
        rNum /= n # n으로 나누어떨어진 남은 rNum을 rNum 자기자신에게 할당
    
    else: # 나누어떨어지지 않는다면
        n += 1 # n에다 1 더해주고 반복 진행
        
print(f'soinList: {soinList}') # 소인수 출력

# 지수 출력
tempNum = 0
for s in soinList: # 소인수 리스트에 있는 소인수를 하나씩 반복
    if tempNum != s: # 참고로, 처음엔 당연히 같지 않을 것이다 tempNum은 0이니까
        # soinList.count(s) # 같지 않다면, 소인수 리스트에 s가 몇 개인지 카운트
        print(f'{s}\'s count: {soinList.count(s)}') # 2개라면 '2'가 출력이 될 것이고
        tempNum = s # 그 s를 tempNum에 할당;
        # 그리고 두번째 반복이 될 때, 같은 수라면 넘어가겠고,새로운게 왔을 땐 위 count가 실행되며 ㅅ로운 s를 카운트 하겠다

---

33_최대공약수

# 100부터 1000사이의 2개의 난수에 대해서 공약수와 최대공약수를 출력하고, 그 2개의 난수가 서로소인지 출력하는 프로그램 만들기
# 최대공약수: 공약수 중 가장 큰수
# 서로소: 1외에 공약수가 없는 것
import random

rNum1 = random.randint(100, 1000)
rNum2 = random.randint(100, 1000)
print(f'rNum1: {rNum1}')
print(f'rNum2: {rNum2}')

maxNum = 0 # 최대공약수 구하는 용
# 공약수 구하기
for n in range(1, min(rNum1, rNum2)+1): # min()사용하여 두 난수중 작은 숫자까지로 범위 설정
    if rNum1 % n == 0 and rNum2 % n == 0: # 두 난수 모두에게서 나눠떨어진다면 공통된 약수이니 공약수
        print(f'공약수: {n}')
        maxNum = n # 공약수가 발생 할 때마다 그 숫자를 maxNum에 할당하면, 마지막 숫자가 가장 큰 숫자이니 최대공약수
# 최대공약수 출력
print(f'최대공약수: {maxNum}')

# 서로소 출력
if maxNum == 1: # 최대공약숙사 1이라면, 공통된 약수가 1밖에 없다는 뜻이니
    print(f'{rNum1}과 {rNum2}는 서로소인다.')

---

34_최소공배수

# 100부터 1000사이의 2개의 난수에 대해서 초대공약수와 최소공배수를 출력하는 프로그래 만들기
# 최소공배수: 공배수 중 가장 작은 수 
# 숫자 2개를 곱한 것을 최대공약수로 나누면 최소공배수를 구할 수 있다
import random

rNum1 = random.randint(100, 1000)
rNum2 = random.randint(100, 1000)
print(f'rNum1: {rNum1}')
print(f'rNum2: {rNum2}')

maxNum = 0 # 최대공약수 구하는 용
# 공약수 구하기
for n in range(1, min(rNum1, rNum2)+1): # min()사용하여 두 난수중 작은 숫자까지로 범위 설정
    if rNum1 % n == 0 and rNum2 % n == 0: # 두 난수 모두에게서 나눠떨어진다면 공통된 약수이니 공약수
        print(f'공약수: {n}')
        maxNum = n # 공약수가 발생 할 때마다 그 숫자를 maxNum에 할당하면, 마지막 숫자가 가장 큰 숫자이니 최대공약수
# 최대공약수 출력
print(f'최대공약수: {maxNum}')

# 최소공배수 구하기
minNum = (rNum1 * rNum2) // maxNum # 두 난수를 곱한 것을 최대공약수로 나눈 몫이 최소공배수
print(f'최소공배수: {minNum}')

---

35_진법

# 사용자가 입력한 수를 이용해서, 다음 내용에 따라 진법 변환하는 코드를 작성해보자
# 진법 관련 함수를 이용해서 진법 변환을 쉽게 할 수 있다.
'''
10진수 --> 2, 8, 16진수 변환
x진수 --> 10진수
X진수 --> x진수
'''
dNum = int(input('10진수 입력:'))

# 10진수 --> 2,8,16진수로 변환
print('2진수: {}'.format(bin(dNum)))
print('8진수: {}'.format(oct(dNum)))
print('16진수: {}'.format(hex(dNum)))

# X진수 --> 10진수
print('2진수(0b10101) -> 10진수({})'.format(int('0b10101', 2))) # int('문자열', 2): 이 문자열의 형태는 2진수이다 라는 것
print('8진수(0o135) -> 10진수({})'.format(int('0o135', 8)))
print('16진수(0x5f) -> 10진수({})'.format(int('0x5f', 16)))

# X진수 --> X진수
print('2진수(0b10101) -> 8진수({})'.format(oct(0b10101))) # 진수 변환 함수(e.g. oct())에 숫자를 그대로 입력
print('2진수(0b10101) -> 10진수({})'.format(int(0b10101)))
print('2진수(0b10101) -> 16진수({})'.format(hex(0b10101)))

print('8진수(0o135) -> 2진수({})'.format(bin(0o135)))
print('8진수(0o135) -> 10진수({})'.format(int(0o135)))
print('8진수(0o135) -> 16진수({})'.format(hex(0o135)))

print('16진수(0x5f) -> 2진수({})'.format(bin(0x5f)))
print('16진수(0x5f) -> 8진수({})'.format(oct(0x5f)))
print('16진수(0x5f) -> 10진수({})'.format(int(0x5f)))

---

36_등차수열

# 다음 수열의 일반항을 구하고 n번째 항의 값과 합을 구하는 프로그램을 만들자
# 등차수열: 일정한 공차를 가지는 수열
'''
{4, 10, 16, 22, 28,...}

등차수열의 일반항: an = a1 + (n-1) * d
등차수열의 합: sn = n(a1 + an) / 2
'''
inputA1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

valueN = 0 # n번째 항의 값
sumN = 0 # n번째 항까지의 합
n = 1
while n <= inputN:
    
    if n == 1 :
        valueN = inputA1 # 첫번째 항에 대한 초기값을 설정 한 것
        sumN += valueN
        print('{}번재 항의 값: {}'.format(n, valueN))
        print('{}번재 항까지의 합: {}'.format(n, sumN))
        n += 1
        continue
    # n이 1이 아닌 이후부턴
    valueN += inputD
    sumN += valueN
    print('{}번재 항의 값: {}'.format(n, valueN))
    print('{}번재 항까지의 합: {}'.format(n, sumN))
    n += 1

print('{}번재 항의 값: {}'.format(inputN, valueN))
print('{}번재 항까지의 합: {}'.format(inputN, sumN))

# 공식 이용
'''
{4, 10, 16, 22, 28,...}

등차수열의 일반항: an = a1 + (n-1) * d
등차수열의 합: sn = n(a1 + an) / 2
'''
inputA1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

# 등차수열의 일반항
valueN = inputA1 + (inputN - 1) * inputD
print('{}번재 항의 값: {}'.format(inputN, valueN))

# 등차수열의 합
sumN = inputN * (inputA1+valueN) / 2
print('{}번재 항까지의 합: {}'.format(inputN, int(sumN)))

---

37_등비수열

# 다음 수열의 일반항을 구하고 n번째 항의 값과 합을 구하는 프로그램 만들기
# 등비수열: 일정한 공비를 가진 수열
'''
{2, 6, 18, 54, 162,...}

등비수열의 일반항: an = a1 * r^(n-1)
등비수열의 합: sn = a1 * (1-r^n) / (1-r)
'''
inputA1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

valueN = 0
sumN = 0
n = 1
while n <= inputN:
    
    if n == 1:
        valueN = inputA1 # 첫번째 항에 대한 초기 설정
        sumN += valueN
        print('{}번째 항의 값: {}'.format(n, valueN))
        print('{}번째 항까지의 합: {}'.format(n, sumN))
        n += 1
        continue
    # 이후부턴 여기가 실행
    valueN *= inputR
    sumN += valueN
    print('{}번째 항의 값: {}'.format(n, valueN))
    print('{}번째 항까지의 합: {}'.format(n, sumN))
    n += 1

print('{}번째 항의 값: {}'.format(inputN, valueN))
print('{}번째 항까지의 합: {}'.format(inputN, sumN))

# 공식 이용
'''
{2, 6, 18, 54, 162,...}

등비수열의 일반항: an = a1 * r^(n-1)
등비수열의 합: sn = a1 * (1-r^n) / (1-r)
'''
inputA1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

valueN = inputA1 * (inputR ** (inputN-1))
print('{}번째 항의 값: {}'.format(inputN, valueN))

sumN = inputA1 * (1-(inputR ** inputN)) / (1-inputR)
print('{}번째 항까지의 합: {}'.format(inputN, int(sumN)))

---

38_시그마

# 첫 째날 쌀 두톨을 받고 둘째 날부터는 하루 전의 2배에 해당하는 쌀을 받는다고 할 때,
# 30일째 되는 날 받게되는 쌀의 개수를 수열과 시그마로 나타내고 이를 출력하는 프로그램 만들기
# 시그마: 수열의 합을 나타내는 기호
'''
{2, 4, 8, 16, 32, 64,...}
'''
inputA1 = int(input('a1 입력:'))
inputR = int(input('공비 입력:'))
inputN = int(input('n 입력:'))

valueN = 0; sumN = 0
n = 1
while n <= inputN:
    if n == 1:
        valueN = inputA1
        sumN = valueN
        print('{}번째 항까지의 합: {}'.format(n, sumN))
        n += 1
        continue
    valueN *= inputR
    sumN += valueN
    print('{}번째 항까지의 합: {}'.format(n, sumN))
    n += 1
print('{}번째 항까지의 합: {}'.format(inputN, format(sumN, ',')))

# 공식 이용
# 등비수열의 합: sn = a1 * (1-r^n) / (1-r)
inputA1 = int(input('a1 입력:'))
inputR = int(input('공비 입력:'))
inputN = int(input('n 입력:'))

sumN = inputA1 * (1 - (inputR ** inputN)) / (1 - inputR)
print('{}번째 항까지의 합: {}'.format(inputN, format(sumN, ',')))

---

39_계차수열

# 다음 수열의 일반항을 구하고, n항의 값을 출력하는 프로그램 만들기
# 계차수열: 두 항의 차로 이루어진 또 다른 수열
# 계차수열의 1항부터 n-1항까지의 합을 구하면 an의 일반항의 값을 알 수 있다
# 등차수열의 일반항 공식: an = a1 + (n-1)d
'''
{2, 5, 11, 20, 32, 47, 65, 86, 110, 137, 167...}
an = {2, 5, 11, 20, 32, 47, 65, 86, 110, 137, 167...}
bk = 3, 6, 9, 12,...

k=1 부터 n-1까지의 시그마 bk = an-a1
'''
# an = a1 + (n-1)d 공식을 적용해 보면, an = 3 + (n-1)3 --> an = 3n
# sn = n(a1 + an) / 2 공식을 이용하여 --> (n-1)(3 + 3(n-1)) / 2 --> (n-1)3n / 2 --> (3n^2 - 3n) / 2
# 이 (3n^2 - 3n) / 2 가 = an-2 이니 --> an = (3n^2 - 3n + 4 ) / 2 --> 이것이 수열 a의 일반항을 구한 것
# an = (3n^2 - 3n + 4 ) / 2으로 첫번째 항 값을 구해보면, n=1을 대입해 보면 (3-3+4)/2 가 되서 2가 나오고,
# n=2를 대입해 보면, (12-6+4)/2 = 5

# an = (3n^2 - 2n + 4) / 2
inputA1 = int(input('a1 입력:'))
inputN = int(input('an 입력:'))

valueN = ((3 * inputN ** 2) - (3 * inputN) + 4) / 2
print('an의 {}번째 항의 값: {}'.format(inputN, int(valueN)))

---

40_피보나치수열

# 피보나치수열에서 n항의 값과 n항까지의 합을 출력하는 프로그램 만들기
# 피보나치수열: 현재 항의 값은 (전 항의 값) + (전전 항의 값)의 합계 
# an = a(n-2) + a(n-1)
'''
{1, 1, 2, 3, 5, 8, 13, 21, 34,...}
'''
inputN = int(input('n입력:'))

valueN = 0; sumN = 0

valuePreN2 = 0 # 전전의 값
valuePreN1 = 0 # 전의 값

n = 1
while n <= inputN:
    if n == 1 or n == 2: # 첫번째, 두번째 항은 값이 1
        valueN = 1
        valuePreN2 = valueN # 전전 항과
        valuePreN1 = valueN # 전 항 모두 일단은 1로 할당
        sumN += valueN # 첫번째 항에선 1, 두번째 항에선 1+1이 되어 2
        n += 1
    else:
        valueN = valuePreN2 + valuePreN1 # 세번째 항부터 전, 전전 항의 값의 합계로 계산
        valuePreN2 = valuePreN1 # 이어서, 전 값이 전전 값이 되고
        valuePreN1 = valueN # 전 값은 현재 값으로
        sumN += valueN
        n += 1
        
print('{}번째 항의 값: {}'.format(inputN, valueN))
print('{}번째 항까지의 합: {}'.format(inputN, sumN))

---

41_군 수열

# 다음 수열을 보고 수열의 합이 최초 100을 초과하는 n번째 항의 값과 n을 출력하는 프로그램을 만들자
# 군 수열: 묶었을 때 그 안에서 규칙성이 있는 수열
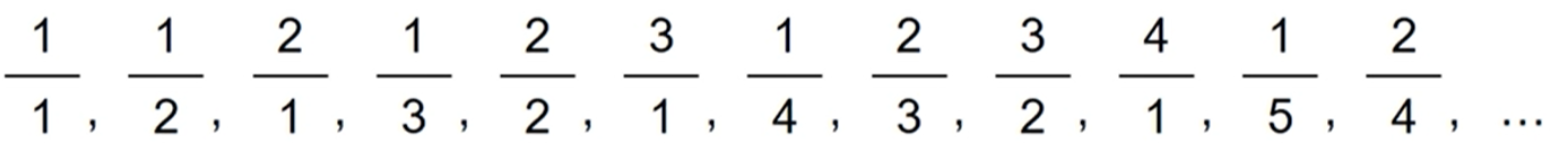
flag = True
n = 1 # 군을 의미; 
nCnt = 1 # 각 항이 될 변수
searchNC = 0 # 분자의 값이 될 변수
searchNP = 0 # 분모의 값이 될 변수
sumN = 0
while flag:
    for i in range(1, n+1): # 1~n까지 반복; 2군이면 2번 반복, 3군이며 3번 반복
        print('{}/{} '.format(i, (n-i+1)), end='') # 분자는 1부터 1씩 증가, 분모는 n부터 1씩 감소; 자동 개행을 막기위한 end=''설정
    
        sumN += i / (n-i+1) # 수열의 합계
        nCnt += 1 # 항도 1씩 증가

        if sumN > 100: # sumN이 100을 초과하게 되면
            searchNC = i # 마지막 i 값이 분자가 되겠고
            searchNP = n-i+1 # 마지막 n-i+1 값이 분모가 되겠다
            flag = False # 그리고 반복문 중단
            break # 반복문을 빠져나오고
    
    print() # 하나의 군이 반복을 끝나고 나면 개행이 되게 하기 위함
    n += 1 # n에 1추가하며, 다음 군에 대한 for문 실행

print('수열의 합이 최초 100을 초과하는 항, 값, 합: {}항, {}/{}, {}'.format(nCnt, searchNC, searchNP, round(sumN, 2)))

---

42_순열

# 파이썬을 이용해서 다음 순열들의 값을 구하는 프로그램 만들기
# 순열: 어떠한 경우의 수가 있는데 그것을 순서에 맞춰 나열하는 것; 순열은 순서가 중요하다
# 예를 들어, 5개의 카드 중 3개를 뽑는다고 하면, 만드는 방법은 순열에선 5 x 4 x 3이 된다
# 순열의 합계: n(n-1)(n-2)...(n-r+1)
'''
- 9P4
- 6P2
'''
numN = int(input('numN 입력:'))
numR = int(input('numR 입력:'))

result = 1 # 결과에 사용할 변수

for n in range(numN, (numN - numR), -1): # 반복문을 이용해서 계속 곱해나갈 텐데, numN에서 시작해서 numN-numR한 값까지 뒤로 내려간다
    print('n: {}'.format(n))
    result = result * n # 반복문이 돌아가며 9 --> 9x8 --> 9x8x7 이런식으로 되겠다
    
print('result: {}'.format(result))

### 카드 7장을 일렬로 나열하되 2, 4, 7번 카드가 서로 이웃하도록 나열하는 모드 경우의 수를 구하는 프로그램 만들기
'''
[1], [2], [3], [4], [5], [6], [7]
'''
# 2, 4, 7을 하나의 카드로 생각해서 구하면 된다
# 1, (2,4,7), 3, 5, 6 --> (2,4,7)을 하나로 묶고, 이렇게 총 5가지가 되니 5에 대한 순열을 구하면 되고: 5!
# 그리고 (2,4,7) 이 안에서의 2가 앞으로 오니 4가 앞으로 오니 등 경우의 수: 3!
# 즉, 5! x 3! 가 될 것이다

# 첫번째 팩토리얼
fNum1 = int(input('factorial1:')) # 첫번째 팩토리얼을 받겠고
result1 = 1 # 그 결과가 담길 변수

for n in range(fNum1, 0, -1): # 입력한 수부터, 0앞의 1까지 반복하겠다
    # result1 = result1 * n
    result1 *= n
print('result1: {}'.format(result1))

# 두번째 팩토리얼
fNum2 = int(input('factorial2:')) # 첫번째 팩토리얼을 받겠고
result2 = 1 # 그 결과가 담길 변수

for n in range(fNum2, 0, -1): # 입력한 수부터, 0앞의 1까지 반복하겠다
    # result1 = result1 * n
    result2 *= n
print('result1: {}'.format(result2))

print('모든 경우의 수: {}'.format(result1 * result2))

---

43_조합

# 파이썬을 이용해서 다음 조합들의 값을 구하는 프로그램 만들기
# 조합: 순서에 상관없이 r개를 선택해서 배열되는 것
# 서로 다른 n개에서 순서와 상관없이 r개를 고르는 것
# nPr / r! --> 순열을 구한 것을 r의 팩토리얼로 나누면 조합을 구할 수 있다
'''
- 9C4
- 6C2
'''
numN = int(input('numN 입력:'))
numR = int(input('numR 입력:'))

resultP = 1 # 순열의 결과를 담을 변수; 순열에 대한 팩토리얼
resultR = 1 # R에 대한 팩토리얼
resultC = 1 # 조합의 결과를 담을 변수

# 순열 계산
for n in range(numN, (numN-numR), -1):
    resultP = resultP * n
print('resultP: {}'.format(resultP)) # 9개 중에서 4개를 뽑았을 때 순서에 맞춰서 나열할 수 있는 경우의 수

# R의 팩토리얼 계산
for n in range(numR, 0, -1):
    resultR = resultR * n
print('resultR: {}'.format(resultR)) # R의 팩토리얼

# 조합 계산
resultC = int(resultP / resultR)
print('resultC: {}'.format(resultC))

# 카드 7장 중 3장을 선택했을 때 3,4,5가 동시에 선택 될 수 있는 확률은?
# 순서에 상관없다
# 카드가 3개가 선택되는 조합의 전체 경우의 수를 구하고 그 중에서 3,4,5가 선택되는 그 확률을 구하면 된다.
'''
[1], [2], [3], [4], [5], [6], [7]
'''
# 위에서 작성한 것 그대로 사용
numN = int(input('numN 입력:'))
numR = int(input('numR 입력:'))

resultP = 1 # 순열의 결과를 담을 변수; 순열에 대한 팩토리얼
resultR = 1 # R에 대한 팩토리얼
resultC = 1 # 조합의 결과를 담을 변수

# 순열 계산
for n in range(numN, (numN-numR), -1):
    resultP = resultP * n
print('resultP: {}'.format(resultP)) # 9개 중에서 4개를 뽑았을 때 순서에 맞춰서 나열할 수 있는 경우의 수

# R의 팩토리얼 계산
for n in range(numR, 0, -1):
    resultR = resultR * n
print('resultR: {}'.format(resultR)) # R의 팩토리얼

# 조합 계산
resultC = int(resultP / resultR)
print('resultC: {}'.format(resultC)) # 35가지의 경우의 수

# 전체 35가지의 경우의 수 중에서, 3,4,5가 같이 나올 수 있는 경우는 1가지이다
result = (1/resultC) * 100 # 1/35
print('{}%'.format(round(result, 2)))

• 참고로, 순열과 조합을 계산해 주는 Math라는 Python 함수들이 있다

---

44_확률

# 박스에 '꽝'이 적힌 종이가 6장 있고, '선물'이 적힌 종이가 4장이 있을 때, 파이썬을 이용해서 '꽝' 3장과 '선물' 3장을 뽑는 확률(%)을 출력하자
# 확률: 전체 사건/표본 공간에서 특정한 사건이 일어날 수 있는 경우의 수를 찾는 것
# 순서가 의미가 없기에 조합을 구하면 된다.
'''
 꽝  | 꽝 | 선물 |  꽝  | 선물
선물 | 꽝 |  꽝  | 선물 |  꽝
'''
# (1번) 전체 10장, 경우의 수에 대해 6가지의 경우를 뽑을 수 있는 조합을 먼저 구하고,
# (2번) 꽝 총 6개 중에 꽝 3장을 뽑을 경우의 수는를 구하고,
# (3번) 선물 총 4개 중에 선물 3장을 뽑을 경우의 수 구해야 한다
# (2번 x 3번) 곱한 것을 (1번)으로 나누어주면 전체의 경우의 수에 대해 특정 사건(꽝 3장, 선물 3장을)을 뽑을 수 있는 경우의 수를 구할 수 있다

# 따라서, nCr 을 구하는 과정이 3번 필요하다
# 3개 따로 코드를 생성하는 것보다 함수를 생성해서 사용하자
def proFun():
    numN = int(input('numN 입력:'))
    numR = int(input('numR 입력:'))

    resultP = 1 # 조합을 구하기 위해 순열이 필요하니 
    resultR = 1 # R!을 구할 것
    resultC = 1 # 조합의 값을 답을 것

    # 순열(P)
    for n in range(numN, (numN-numR), -1):
        resultP = resultP * n
    print('resultP: {}'.format(resultP))

    # R!
    for n in range(numR, 0, -1):
        resultR = resultR * n
    print('resultR: {}'.format(resultR))

    # 조합(C)
    resultC = int(resultP / resultR)
    print('resultC: {}'.format(resultC))

    return resultC

# 먼저 전체의 경우의 수를 나타내는 것을 진행해보자 (10C6)
sample = proFun()
print('sample: {}'.format(sample)) # 결과: 210가지

# 이제 특정 사건 중 첫번째 사건의 경우의 수 (6C3)
event1 = proFun()
print('sample: {}'.format(event1)) # 결과: 20가지

# 이제 특정 사건 중 두번째 사건의 경우의 수 (4C3)
event2 = proFun()
print('sample: {}'.format(event2)) # 결과: 4가지

# 확률 계산
probability = (event1 * event2) / sample
print('probability: {}%'.format(round(probability * 100, 2))) # 결과: 38.1%