1. 피보나치 수열
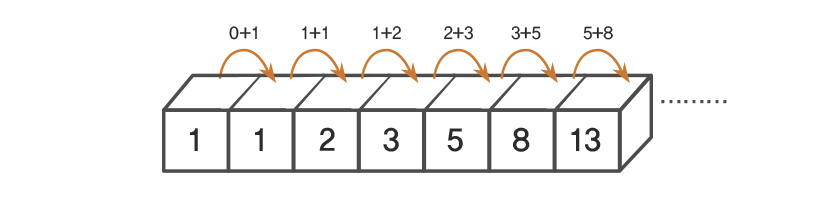
수학에서 피보나치 수는 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다. 처음 여섯 항은 각각 1, 1, 2, 3, 5, 8이다.
2. 배열을 이용하여 구현
int[] arr = new int[n];
arr[0] = 1;
arr[1] = 1;
for (int i = 2; i < n; i++) {
arr[i] = arr[i - 2] + arr[i - 1];
}(1) n이라는 수를 입력받고 n개의 피보나치 수열을 출력한다는 가정하에 n의 크기를 가진 배열을 생성한다.
(2) 피보나치 수열에서 처음 두 자리를 1로 초기화한다.
(3) 반복문을 돌면서 arr[i]에 arr[i] 이전 두 개의 수를 더하여 arr[i]를 초기화한다.
3. 배열을 이용하지 않은 구현
int a = 1;
int b = 1;
int c = 0;
for (int i = 2; i < n; i++) {
c = a + b;
a = b;
b = c;
}(1) int형 변수 a, b, c를 선언한다. a와 b는 최초 두 자리 수이며 1로 초기화한다.
(2) 반복문을 돌면서 c를 a + b 값으로 초기화한다.
(3) 반복문 안에서 c를 초기화한 후 a를 b로 b를 c로 초기화한다.
4. 재귀함수를 이용한 구현
static int[] arr = new int[n];
public int fibo(int n) {
if (arr[n] > 0) {
return arr[n];
}
if (n == 1 || n == 2) {
arr[n] = 1;
} else {
arr[n] = fibo(n - 1) + fibo(n - 2); // 재귀호출
}
return arr[n];(1) 불필요한 계산을 피하기 위해(이미 계산된) 계산된 값을 저장할 배열을 선언한다.
(2) 재귀호출을 반복하다가 n이 1이나 2가 될 경우 1을 리턴한다. 이 값을 더하여 리턴하고 리턴하고 재귀를 하다보면 피보나치 수열이 완성된다. (스택 프레임을 그려보며 재귀함수 호출하는 작업을 그려보면 이해가 빠르다.)
Reference
https://ko.wikipedia.org/wiki/%ED%94%BC%EB%B3%B4%EB%82%98%EC%B9%98_%EC%88%98
https://news.samsungdisplay.com/23402
