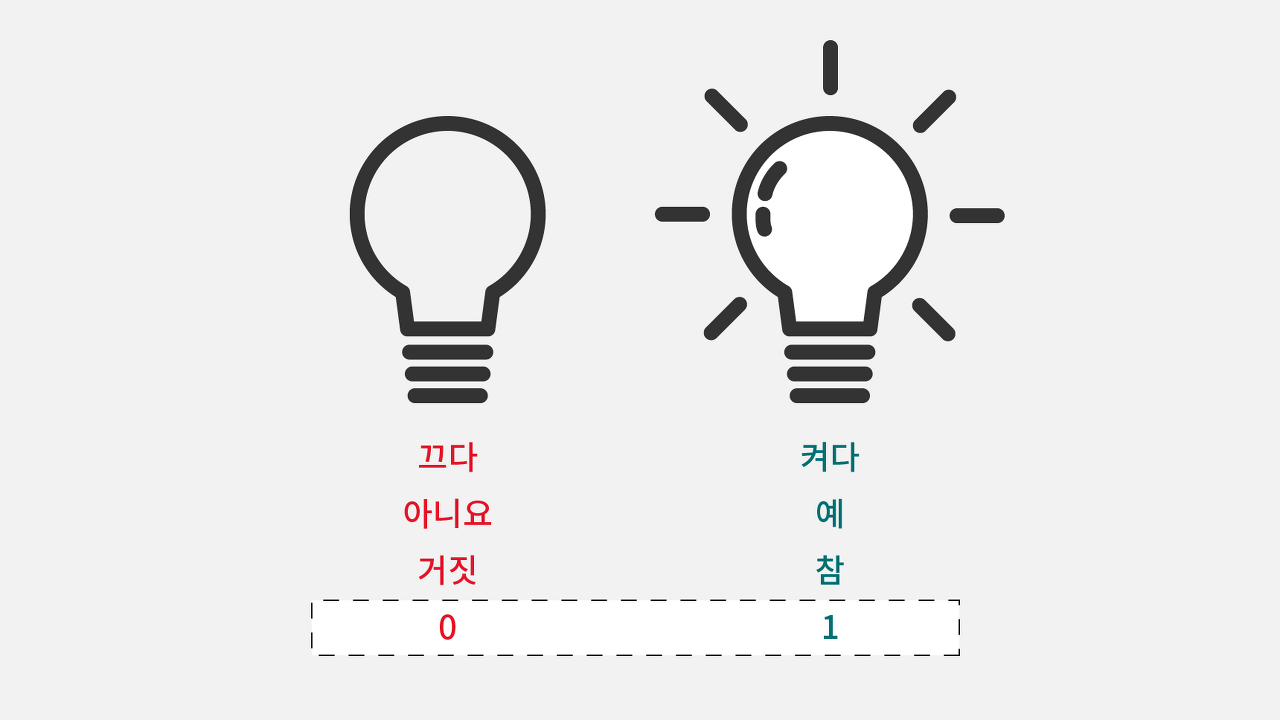
디지털 시스템은 모든 유형의 정보값을 숫자로 표현합니다.
컴퓨터는 2진수(binary number)를 기반으로 설계가 되었는데
컴퓨터의 논리회로가 전기 신호가 있을 경우를 1/ 없을 경우를 0로 인식하기 때문입니다 :)
만약 2진수가 아닌 N진수의 전기신호를 받게 된다면 데이터 처리과정에서 처리시간이 길어지고 정확한 전압을 측정하는데 비용이 많이 발생되어 비효율적입니다.
2진수의 원리를 알면 우리가 실제로 사용하는 10진법과 다르지 않으니
어렵게 생각하지 말자고 하는게 이번 챕터의 의도/목적으로 보입니다 (잘은 되지 않겠지만....)

비트는 이진 숫자라는 뜻을 축약한 단어로 디지털 정보를 표현하는 가장 작고 기본적인 단위입니다.
이진 단어는 두개의 값을 가졌음을 암시합니다. 접두사 bi는 2를 상징하죠 :)
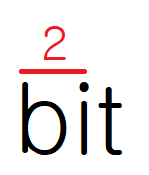
비트 0 또는 1의 값 중 하나의 값을 사용하고, 나머지는 사용하지 않는 숫자입니다.
두개의 값 중 하나를 선택하는 정보라면 무엇이든 이 작은 단위인 비트 한개로 인코딩하거나 표현할 수 있습니다.

< 켜짐/꺼짐, 참/거짓, 예/아니오, 높음/낮음, 안/밖, 위/아래 ......else>
단일 비트로 이진 선택을 충분히 나타낼 수 있지만 우리는 더 많은 선택지를 표시하거나
복잡한 정보를 표현할 방법이 필요합니다.
그러기 위해서 이 비트 단위를 여러개 사용하여 0과 1로 만들 수 있는 다양한 조합에 의미를 할당해 사용합니다.

이 책에서는 미국의 어느 대학을 예시로 이진법의 할당방식을 설명을 했는데
학생을 신입생/2학년/3학년/졸업반과 같이 나눈다면 단 두개의 비트로 00/01/10/11로 표현할 수 있습니다.
만약에 대학원을 추가한다고 가정했을 때, 비트 두개로는 표현하기 어려우니 비트를 추가하여 3자리로 만들면 대학원 뿐만 아니라 교수/직원/박사 후 과정까지 구현이 가능하지요!
(000/001/002 ~ 110/110으로 총 여덟가지를 표현할 수 있음)
이렇게 비트의 개수와 이 비트로 레이블을 붙일 수 있는 항목의 개수는 일정한 관계가 있는데
바로 거듭제곱근입니다. 만일 비트가 N개가 있다면, 표현할 수 있는 비트의 패턴 개수는
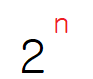
컴퓨터 내부는 이렇게 모든 것이 이진수로 처리되기 때문에
크기와 용량과 같은 속성이 거듭제곱으로 표현되는 경향이 있습니다.
따라서 2의 10승정도 까지만 알아두면 우리는 매우! 편리하답니다! 하하 :D
그 이후에는 근사치를 얻을 수 있는 손쉬운 방법이 있는데, 2의 거듭제곱 중 일부가 10의 거듭제곱에 가까운 값이라는 것, 기억하기 쉽게 규칙적입니다.
수치가 커짐에 따라 오차값이 커지긴 하지만 차이가 미미해서 이 연관 관계는 상당히 폭넓게 유용하게 사용된다고 하네요 :-)
아래는 제가 자료 좀 찾다가 발견한 만화인데 이번 내용이랑도 관련이 있고
새벽에 저에게 큰 웃음을 주어서ㅋㅋ
여러분들도 같이 웃으시라고 남겨 놓습니다.
그럼 오늘의 정리 끝! 빠잉! 'ㅇ'
