polynomial in C

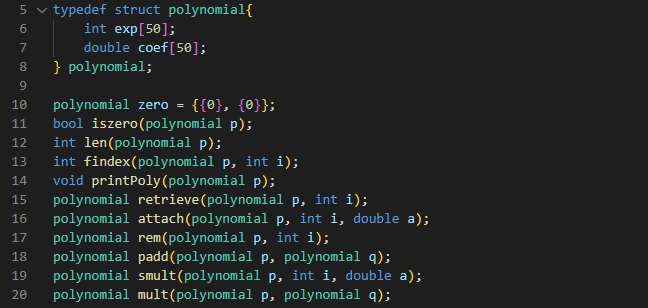
코드

#include <stdio.h>
#include <stdbool.h>
#include <math.h>

typedef struct polynomial{
    int exp[50];
    double coef[50];
} polynomial;

polynomial zero = {{0}, {0}};
bool iszero(polynomial p);
int len(polynomial p);
int findex(polynomial p, int i);
void printPoly(polynomial p);
polynomial retrieve(polynomial p, int i);
polynomial attach(polynomial p, int i, double a);
polynomial rem(polynomial p, int i);
polynomial padd(polynomial p, polynomial q);
polynomial smult(polynomial p, int i, double a);
polynomial mult(polynomial p, polynomial q);

int main() {
    polynomial p = {{4, 2, 0}, {2, -1, 3}};
    polynomial q = {{5, 3, 2, 0}, {1, 1, 1, 1}};
    printPoly(p);
    printPoly(q);
    printPoly(mult(p, q));
}

bool iszero(polynomial p){
    if((p.exp[0]==0) && (p.coef[0]==0.0)){
        return true;
    }
    else return false;
}

int len(polynomial p){
    int count =0;
    for(int i = 0; i<p.exp[0]+1; i++){
        if(p.exp[i]!=0){
            count++;
        }
    }
    return count+1;

}

int findex(polynomial p, int i){
    for(int j=0; j<p.exp[0]+1;j++){
        if(p.exp[j]==i){
            return j;
        }
    }
    return -1;
}

polynomial retrieve(polynomial p, int i){
    int j = findex(p,i);
    if(j==-1){
        return zero;
    }
    else return (polynomial){{i}, {p.coef[j]}};
}

void printPoly(polynomial p){
    int n = len(p);
    printf("\n");
    printf("%.1lf", p.coef[0]);
    if(p.exp[0]!=0) printf(" x ^ %d", p.exp[0]);
    for(int i = 1; i< n; i++){
        printf ("%s", (p.coef[i]>=0)? " +":" -");
        printf(" %.1lf", fabs(p.coef[i]));
        if(p.exp[i]!=0) printf(" x ^ %d", p.exp[i]);
    }
    printf("\n");
}

polynomial attach(polynomial p, int i, double a){
    polynomial r = zero;

    if(a ==0) return p;
    for(int j=0; j<len(p); j++){
        if(p.exp[j]>i){
            r.exp[j]=p.exp[j];
            r.coef[j]=p.coef[j];
        }
        else if(p.exp[j]==i){
            r.exp[j]=i;
            r.coef[j]=a;
            for(int k=j+1; k<len(p); k++){
                r.exp[k]=p.exp[k];
                r.coef[k]=p.coef[k];
            }
            break;
        }
        else if(p.exp[j]<i){
            r.exp[j]=i;
            r.coef[j]=a;
            for(int k=j; k<len(p); k++){
                r.exp[k+1]=p.exp[k];
                r.coef[k+1]=p.coef[k];
            }
            break;
        }
    }
    return r;
}

polynomial rem(polynomial p, int i){
    polynomial r = zero;
    int x = findex(p,i);
    if(x==-1) return p;
    else{
        for(int j=0;j<len(p);j++){
            if(p.exp[j]>i){
                r.exp[j]=p.exp[j];
                r.coef[j]=p.coef[j];
            }
            else if(p.exp[j]<=i){
                r.exp[j]=p.exp[j+1];
                r.coef[j]=p.coef[j+1];
            }
        }
        return r;
    }
}

polynomial padd(polynomial p, polynomial q){
    polynomial r=zero;
    while(!iszero(p)||!iszero(q)){
        if(p.exp[0]>q.exp[0]){
            r = attach(r, p.exp[0], p.coef[0]);
            p = rem(p, p.exp[0]);
        }
        else if(p.exp[0]==q.exp[0]){
            r = attach(r, p.exp[0], p.coef[0]+q.coef[0]);
            p = rem(p, p.exp[0]); q = rem(q, q.exp[0]);
        }
        else if(p.exp[0]<q.exp[0]){
            r = attach(r, q.exp[0], q.coef[0]);
            q = rem(q, q.exp[0]);
        }
    }
    return r;
}


polynomial smult(polynomial p, int i, double a){
    polynomial r=zero;
    while(!iszero(p)){
        r = attach(r, p.exp[0]+i, a*p.coef[0]);
        p = rem(p,p.exp[0]);
    }
    return r;
}


polynomial mult(polynomial p, polynomial q){
    polynomial r = zero;
    while(!iszero(q)){
        r = padd(r, smult(p, q.exp[0], q.coef[0]));
        q = rem(q, q.exp[0]);
    }
    return r;
}

결과

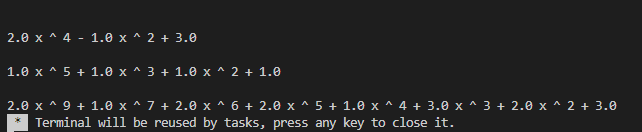
오답노트

• bool 함수 else false; -> else return false; : false 대신 임의의 값 (계산시 불러왔던 정수값)이 반환됨으로써 결과값이 틀림.
• rem(q, q.exp[0]) -> q = rem(q, q.exp[0]) : 반환한 값을 저장해주어야 무한반복 되지않고 zero에 도달 가능.
• mult함수 무한반복문제 : 껐다 켰더니 해결됨 (아마 메모리 문제?)