gpt가 fractal과 어울리는 곡으로 coldplay의 clocks를 추천했다.
반복적인 피아노 리프와 점진적인 구조가 프랙탈적 느낌을 준다고 한다.
ai에게 노래도 추천 받을 수 있고 참 좋은 세상이다..

fractal이란

자기유사성을 갖는 기하학적 구조
이게 20세기의 수학이구나. 까마득함을 느꼈다.
여기에 정리한 것은 이 까마득한 수학의 일부 중에 일부이며, 완전히 이해하고 정리한 것이 아니므로 틀린 부분이 존재할 수도 있다.
정리를 하되 출처를 기입하고 내가 그릴 프랙탈을 이해할 정도로만 탐구했다.

주요 프랙탈 발표 순서

1. Cantor Set(1872)

• 독일 수학자 Georg Cantor가 처음 제안한 집합
• 자기 유사성을 가진 최초의 수학적 구조

2. koch Curve(1904)

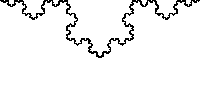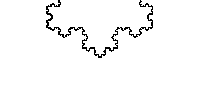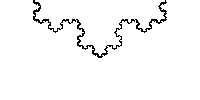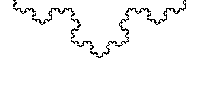
• 스웨덴 수학자 Helge von koch가 발표
• 삼각형 모양을 반복적으로 추가하여 만들어지는 곡선

3. Sierpiński Triangle and Carpet 시에르핀스키 삼각형 및 카펫(1915~1916)

• 폴란드 수학자 Wacław Sierpiński 제안
• 삼각형과 사각형을 분할하여 생성되는 구조

4. Julia Set(1918)

• 프랑스 수학자 Gaston Julia와 Pierre Fatou가 연구
• 복소수 함수의 반복 결과로 생성되는 구조. 망델브로 집합과 밀접한 연관
• 이 당시 컴퓨터가 없었기 때문에 이론 연구는 했지만, 시각적으로 표현하는 것은 불가능했다.

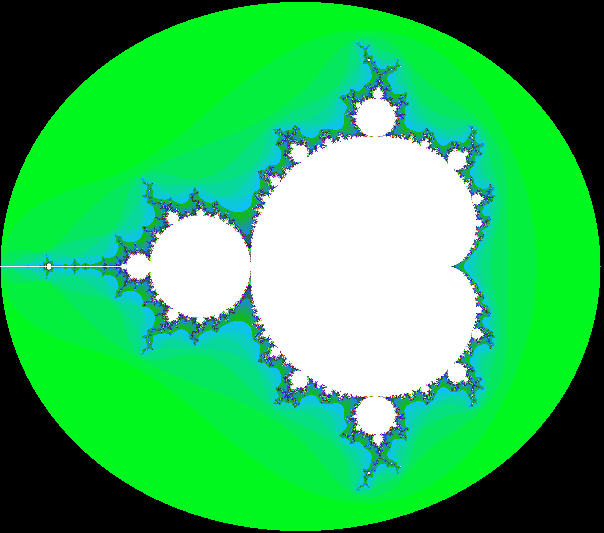
5. Mandelbrot Set(1980)

• 브누아 망델브로가 컴퓨터를 이용해 시각화한 유명한 프랙탈. 복소수 평면에서 함수의 반복을 시각화하다가 발견. 줄리아 집합을 연구했다!
• 복소수 평면에서 특정 함수의 반복 결과로 생성되는 구조.
• 프랙탈 용어를 망델브로가 처음 사용함.

내가 그리는 프렉탈

mandelbrot set

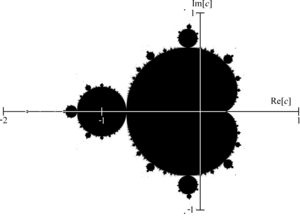
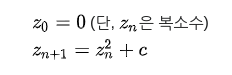
• 브누아 망델브로가 고안한 프랙탈의 일종
• 위 점화식으로 정의된 수열이 발산하지 않는 성질을 갖도록 하는 복소수 c의 집합
• 망델브로 집합 외부: $z_n$의 절대값이 2보다 크면 $z_n$이 발산한다고 말할 수 있다. 이 때의 2는 경계값이라고 한다. $z_n$의 n값에 따라 망델브로 집합 바깥의 영역을 다른 색으로 칠한다. 예컨대, 가장 빨리 발산하는 점은 어두운 색으로 발산 속도가 느려질수록 밝은 색으로 칠하는데, 이로 인해 경계선 근처에 복잡하고 다채로운 색상 패턴이 나타난다.(카오스 현상)
• 망델브로 집합 내부: $z_n$은 무한히 계산해도 끝나지 않아서 정확하게 계산된 것이 아니라 근사한 집합만 가질 수 있다. 위 그림에서는 검정색에 해당하고, 해당 c들은 망델브로 집합에 속한다고 판정한다.
• Julia set의 일종의 지도.

julia set

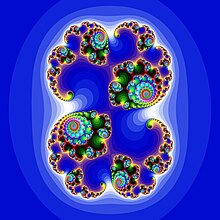
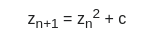
• 주어진 복소수 c에 대해서 다음 점화식에 따라 정의된 수열이 발산하지 않는 성질을 갖도록 하는 복소수 $z_0$의 집합
• 점화식은 망델브로 집합과 같지만, 집합을 이루는 원소가 다르다.(z와 c 잘 구분하기)

Newton-raphson fractal

역사

1. 17세기: Isaac Newton과 Joseph Raphson이 개발한 수치해석 알고리즘
2. 1879: 영국 수학자 Arthur Cayler(1879)가 The Newton-Fourier Imaginary Problem에서 3차 방정식 $z^3 - 1 = 0$에 대해 "복소 평면에서 초기값이 어느 근으로 수렴할지 예측할 수 있는가"라는 문제 제기
3. 1986: John Hubbard와 Adrien Douady가 체계화

일반화

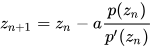
• 모든 뉴턴 프랙탈은 줄리아 집합의 일종이지만, 모든 줄리아 집합이 뉴턴 프랙탈은 아니다.. 하하

시간 매개형 프랙탈

• Escape-time fractals, 궤도 프랙탈: 대개 복소평면 상에서 각각의 점이 발산하는 속도를 색으로 나타낸 이미지
• 준-자기유사적 프랙탈(통계학적 프렉탈 Statistical self-similarity): 자기 유사성의 강도가 낮은 것

만델브로 집합과 줄리아 집합의 연결

정의 차이(헷갈리니 한번 더)

• 만델브로 집합: 특정 복소수 c값에 대해 점화식이 발산하지 않는 c값들의 집합
• 줄리아 집합: 특정 복소수 c값이 주어졌을 때(그래서 만델브로가 지도라고 일컬음), 점화식이 발산하지 않는 초기값 $z_0$들의 경계로 이루어진 집합

mandelbrot exploler

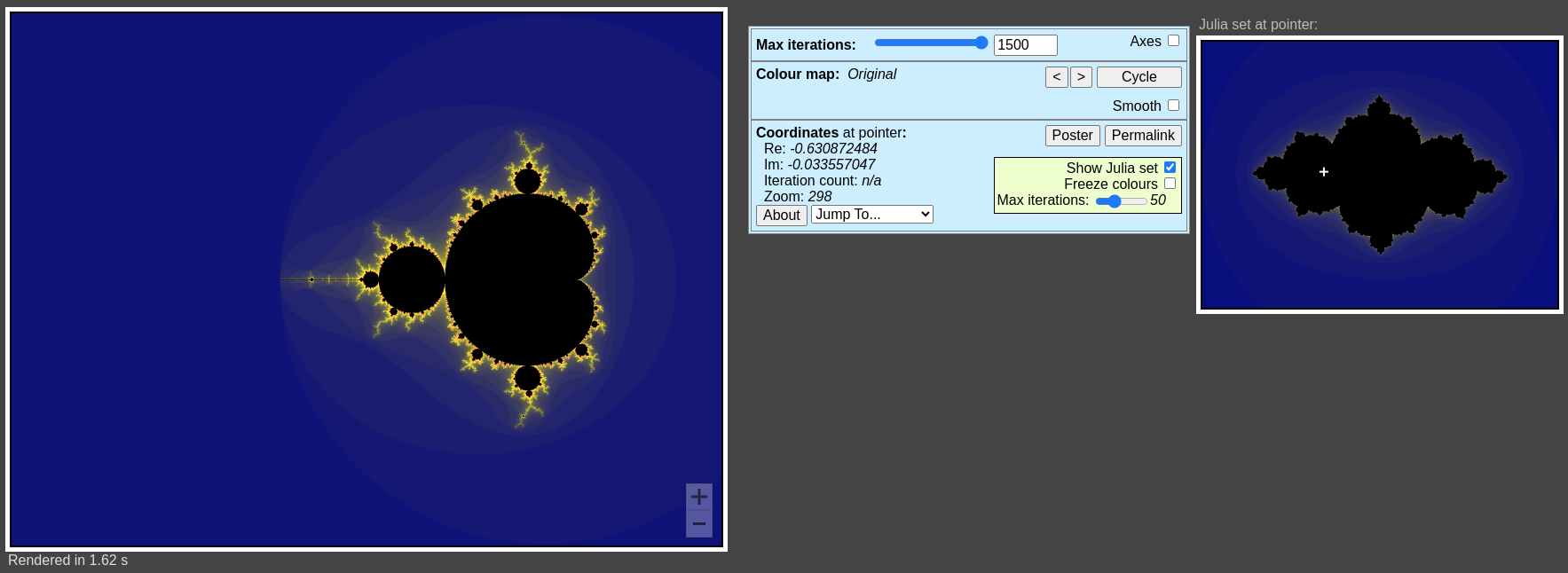
• 만델브로 집합 내부의 c값(검정색 영역): "연결된 형태"의 줄리아 집합 생성

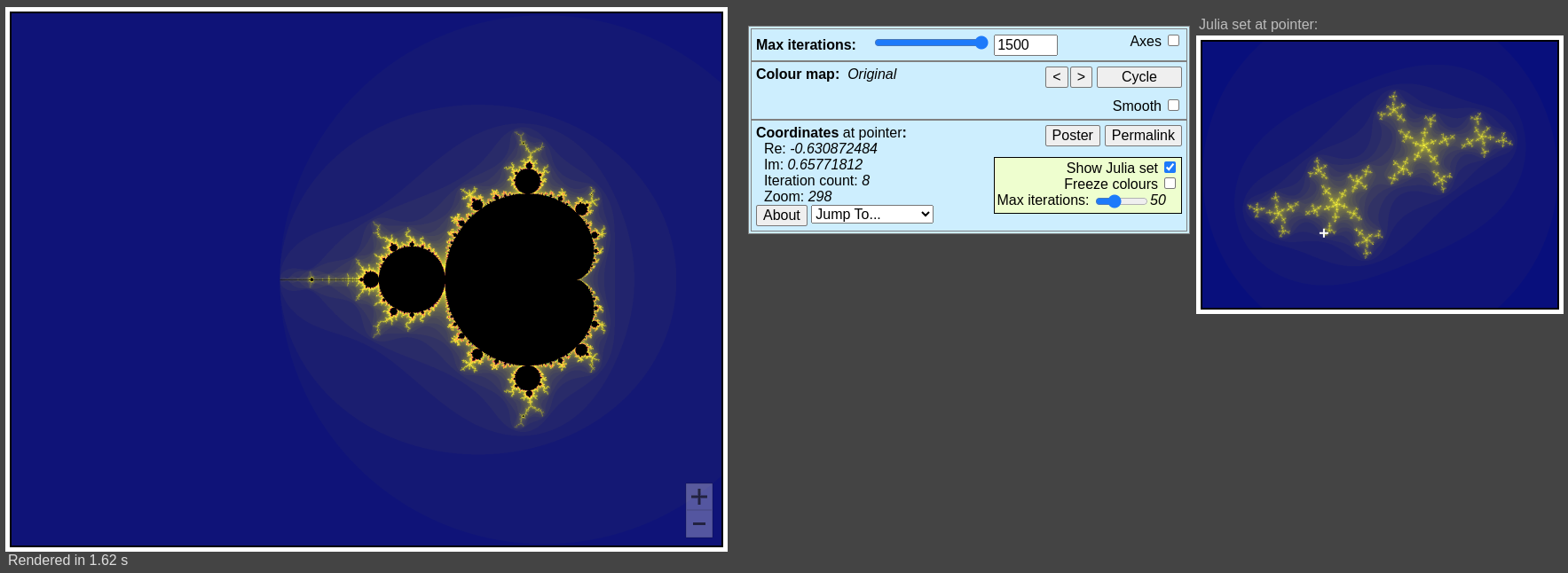
• 만델브로 집합 외부의 c값(검정색 이외의 영역): "분리된 형태"의 줄리아 집합 생성

줄리아 집합이 단위원인 경우!

Cornell University: Julia Sets and the Mandelbrot Set

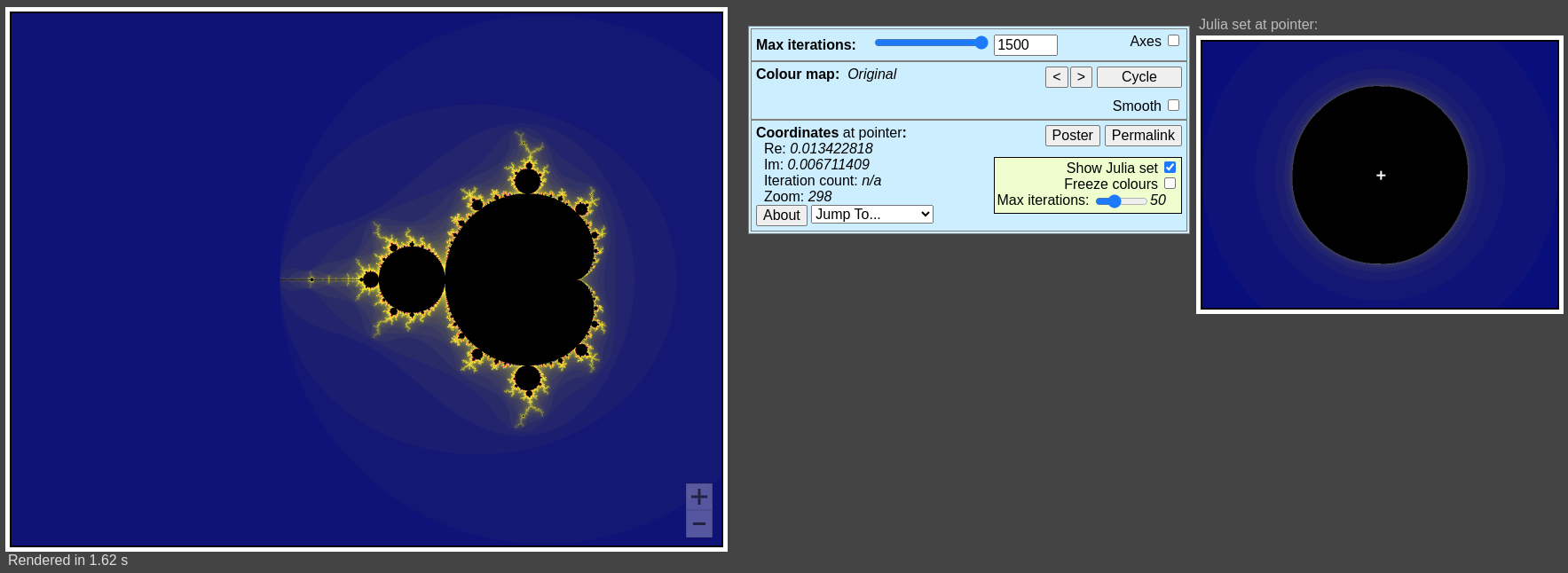
왐마 너무 신기해.

지금 무슨 과제 하고 있나

c언어의 그래픽스 라이브러리로 위 그림과 같이 프랙탈 속에 프랙탈 속에 프랙탈 속에 프랙탈 속에 프랙탈 속에..... 무한히 보일 수 있도록(컴퓨터 한계 내에서) 만들기를 하고 있다.
마우스 휠로 저 그림처럼 나와야 하는데,

• zoom하는 속도가 너무 느려요.
• 이미지 품질이 너무 구리다.

이것이 현실

• 키보드로 색상 변경 가능
• 마우스휠로 zoom in, zoom out을 할 수 있음. zoom을 계속 하다보면 어느 순간 안되는 지점이 생김. (아직 이 기준을 모르겠음)
• 왼쪽, 오른쪽, 위, 아래로 이동은 가능한데... 반응속도가 너무 느림.

완성

화면 녹화해서 업로드.

• 팔레트: 4종류(특정 키를 누르면 팔레트를 순회하게 만듦)

{BLUE, WHITE, LASER_YELLOW}, //wiki랑 유사한 색!
{RED, GREEN, BLUE},
{WHITE, HOT_PINK, CYBER_CYAN},
{BLACK, WHITE, LAVA_RED}

mandelbrot

julia