📖저자님의 책 소개 영상: https://www.youtube.com/watch?v=Q13Uj_5bH9M

🗓️TIL (this week I learned)
수 읽기, 정리, 몸풀기 문제1
목 배열, 해시 복습
금 🤔🤔🤔🤔
토 🤔🤔🤔🤔

• 여기는 풀면서 IQ 상승을 노려볼 만한다🤣

12-1 백트래킹과 백트래킹 알고리즘 개념⭐⭐⭐

🔷 백트래킹: 가능성이 없는 곳에서는 되돌아가고 가능성이 있는 곳을 탐색하는 알고리즘

• 핵심: 해가 될 가능성을 판단하는 것
• 유망 함수(promising function):
  - 유망 = 해가 될 가능성이 있다..
• Constraint Satisfaction Problems (제약 충족 문제): 수많은 제약 조건을 충족하는 상태(states)를 찾아내는 수학 문제.
  - ex) 스도쿠, 십자말 풀이, 8퀸 문제, 4색 문제(지도 색칠), 배낭문제, 문자열 파싱, 조합 최적화 등

🔷 N-퀸 문제: $N*N$체스판에 $N$개를 배치했을 때, 퀸을 놓을 수 있는 경우의 수가 몇 개인지를 찾는 게 논점이다.
참고:
https://cs.lmu.edu/~ray/notes/backtracking/
n-queens wiki(en) -> 책 퀸즈 문제 풀이와 코드가 유사함.

• N개 배치를 놓쳐서 며칠 동안 머리를 싸매고 있었다..ㅠㅠㅠㅠㅠ

• 예컨대, 4x4 체스판, 4개의 퀸을 놓을 수 있는 경우의 수는 4x4x4x4=256(완전탐색). 이를 유망함수를 추가해 탐색 대상을 줄여 해를 구할 수 있다. (4-퀸 문제의 해는 2개)
  
  

• n-queens의 해
  

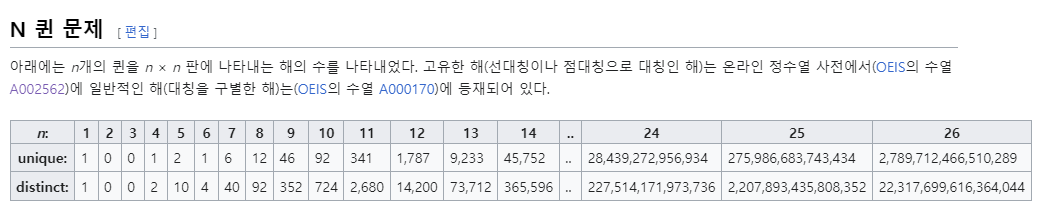
12-2 문제

1. 피로도

https://school.programmers.co.kr/learn/courses/30/lessons/87946

def dfs(cur_k, cnt, dungeons, visited):
    answer_max = cnt
    for i in range(len(dungeons)):
        if cur_k >= dungeons[i][0] and visited[i] == 0:
            visited[i] = 1
            answer_max = max(answer_max, dfs(cur_k - dungeons[i][1], cnt + 1, dungeons, visited))
            visited[i] = 0
    return answer_max
        

def solution(k, dungeons):
    visited = [0]  * len(dungeons)
    answer_max = dfs(k, 0, dungeons, visited)
    return answer_max

순열로도.. (백트래킹은 아님)

import itertools

def solution(k, dungeons):
    max_cnt = 0
    
    for perm in itertools.permutations(dungeons, len(dungeons)):
        cur_k = k
        cnt = 0
        
        for need, cost in perm:
            if cur_k >= need:
                cur_k -= cost
                cnt += 1
            else:
                break
        if cnt > max_cnt:
            max_cnt = cnt
            
        if max_cnt == len(dungeons):
            return max_cnt
    return max_cnt

2. N-퀸

https://school.programmers.co.kr/learn/courses/30/lessons/12952

def backtrack(col_positions, current_row, board_size):
    total_solutions = 0
    if current_row == board_size:
        return 1
    for col in range(board_size):
        col_positions[current_row] = col
        for prev_row in range(current_row):
            same_col = (col_positions[prev_row] == col)
            same_diag = abs(col_positions[prev_row] - col) == current_row - prev_row
            if same_col or same_diag:
                break
        else:
            total_solutions += backtrack(col_positions, current_row + 1, board_size)
    return total_solutions

def solution(n):
    return backtrack([0] * n, 0, n)

3. 양궁대회

https://school.programmers.co.kr/learn/courses/30/lessons/92342

from itertools import combinations_with_replacement
from collections import Counter

def solution(n, info):
    maxdiff, max_comb = 0, {}
    
    # 주어진 조합에서 각각의 점수 계산
    def calculate_score(combi):
        ryon, apeach = 0, 0
        for score in range(1, 11):
            arrows = cnt.get(score, 0)
            if info[10 - score] < arrows:
                ryon += score
            elif info[10 - score] > 0:
                apeach += score
        return ryon, apeach
        
    # 최대 차이와 조합 저장
    def calculate_diff(diff, cnt):
        nonlocal maxdiff, max_comb
        if diff > maxdiff:
            max_comb = cnt
            maxdiff = diff
    # 가능한 라이언의 과녁 점수 조합의 모든 경우에 대해서 체크
    for combi in combinations_with_replacement(range(11), n):
        cnt = Counter(combi)
        score1, score2 = calculate_score(combi)
        diff = score1 - score2
        calculate_diff(diff, cnt)
    
    # 최대 차이가 0이상이 경우, 조합 반환
    if maxdiff > 0:
        answer = [0] * 11
        for n in max_comb:
            answer[10 - n] = max_comb[n]
        return answer
    else:
        return [-1]

4. 외벽점검(고난이도)

https://school.programmers.co.kr/learn/courses/30/lessons/60062

5. 사라지는 발판(고난이도)

https://school.programmers.co.kr/learn/courses/30/lessons/92345

# 어렵.....
def solution(board, aloc, bloc):
    ROW, COL = len(board), len(board[0]) # 게임판의 행, 열 저장
    DR, DC = [-1, 0, 1, 0], [0, 1, 0, -1]
    
    # 주어진 위치가 유효한 위치인가?
    def is_valid_pos(r, c):
        return 0 <= r < ROW and 0 <= c < COL
    
    # 재귀적 호출
    def recursive_func(alpha_pos, beta_pos, visited, step):
        # 현재 플레이어의 위치와 이동 가능 여부와
        # 상대 플레이어가 이긴 경우를 저장하는 변수들
        r, c = alpha_pos if step % 2 == 0 else beta_pos
        can_move = False
        is_opponent_winner = True
        # 이긴 경우와 진 경우 저장하는 리스트
        win_steps, lose_steps = [], []
        
        # 현재 위치에서 이동할 수 있는 모든 방향으로 이동
        for i in range(4):
            nr, nc = r + DR[i], c + DC[i]
            # 이동할 수 있다면
            if is_valid_pos(nr, nc) and (nr, nc) not in visited and board[nr][nc]:
                can_move = True
                # 두 플레이어 위치가 같다면 A가 이김. True, step + 1 반환
                if alpha_pos == beta_pos:
                    return True, step + 1
                # 재귀적으로 호출하여 이긴 여부와 남은 툰수 가져오기
                win, steps_left = (
                    recursive_func([nr, nc], beta_pos, visited | {(r, c)}, step + 1)
                    # 방문한 칸을 기록하는 visited 와 (r, c) 합집합 
                    if step % 2 == 0
                    else recursive_func(
                        alpha_pos, [nr, nc], visited | {(r, c)}, step + 1
                    )              
                )
                # 상대 플레이어가 이긴 경우만 True
                # &= 비트 연산자 복합 대입. 논리적 AND
                is_opponent_winner &= win 
                # 이긴 경우와 진 경우 저장
                (win_steps if win else lose_steps).append(steps_left)
                
        # 만약 이동할 수 있는 위치가 없다면
        if not can_move:
            return False, step
        # 상대 플레이어가 이긴 경우
        if is_opponent_winner:
            return False, max(win_steps)
        # 현재 플레이어가 이긴 경우
        return True, min(lose_steps)
    
    # A 플레이어가 이길 때까지 걸리는 최소 턴 수를 반환
    # _ = 이 값은 사용하지 않을 것이다.
    _, steps = recursive_func(aloc, bloc, set(), 0)
    return steps