STL / 정렬 / 이진 탐색

STL → 컨테이너, 반복자, 알고리즘

pair : 두 가지 값이 하나의 쌍을 이룸
vector : 가변적으로 사용 할 수 있는 배열 (중요!!) -> https://blockdmask.tistory.com/70
deque : 앞, 뒤로 삽입 삭제가 가능 / 단 반복자 사용 불가
set : 트리 구조로 삽입 정렬 시 즉시 정렬, 중복을 허용하지 않음
map : set과 유사하나 key,value로 이루어져 있음

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

pair<string, int> professor;
vector<string> students;
deque<int> dq;
set<int> s;
map<int, string> m;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    
    professor.first = "벨롭이"; professor.second = 55;
    cout << professor.first << "는 " << professor.second << "살!\n";
    
    students.push_back("현수"); students.push_back("준형"); students.push_back("sangchep");
    vector<string>::iterator iter;

    for(int i=0; i<students.size(); i++)
        cout << students[i] << ' ';
    cout << '\n';
    
    students.erase(students.begin());
    for(iter = students.begin(); iter != students.end(); iter++)
        cout << *iter << ' ';
    cout << '\n';
    
    students.pop_back();
    for(string str : students)
        cout << str << ' ';
    cout << '\n';

    dq.push_back(3); dq.push_back(5); dq.push_back(2); dq.push_back(6);
    dq.push_back(1);
    dq.pop_front();
    dq.push_front(9);
    for(int i=0; i<dq.size(); i++) cout << dq[i] << ' ';
    cout << '\n';

    for(int i=9; i>0; i--) {
        s.insert(i);
        m.insert(make_pair(i,"hello"));
    }

    for(int i : s) cout << i << ' ';
    cout << '\n';
    for(pair<int, string> i : m) cout << i.first << ' ' << i.second << '\n';
}

sort : 정렬하는 함수
find : 검색하는 함수
upper_bound : 인자보다 큰 부분의 주소 반환
lower_bound : 인자보다 작은 부분의 주소 반환
binary_search : 이진탐색법으로 주소 반환

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int num[12] = {1,3,5,7,9,13,13,13,16,17,20,22};
int num2[12] = {99,3,5,77,9,3,13,2,16,17,6,22};

int cmp(int a, int b) {
    return a > b;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout << "upper_bound : " << upper_bound(num, num+12, 10)-num << '\n';
    cout << "lower_bound : " << lower_bound(num, num+12, 10)-num << '\n';
    cout << "binary_search : " << binary_search(num, num+12, 10) << "\n\n";

    cout << "upper_bound : " << upper_bound(num, num+12, 13)-num << '\n';
    cout << "lower_bound : " << lower_bound(num, num+12, 13)-num << '\n';
    cout << "binary_search : " << binary_search(num, num+12, 13) << '\n';

    sort(num2,num2+12);
    for(int i=0; i<12; i++) cout << num2[i] << ' ';
    cout << '\n';
    sort(num2, num2+12, cmp);
    for(int i=0; i<12; i++) cout << num2[i] << ' ';

}

이진 탐색(Binary Search)

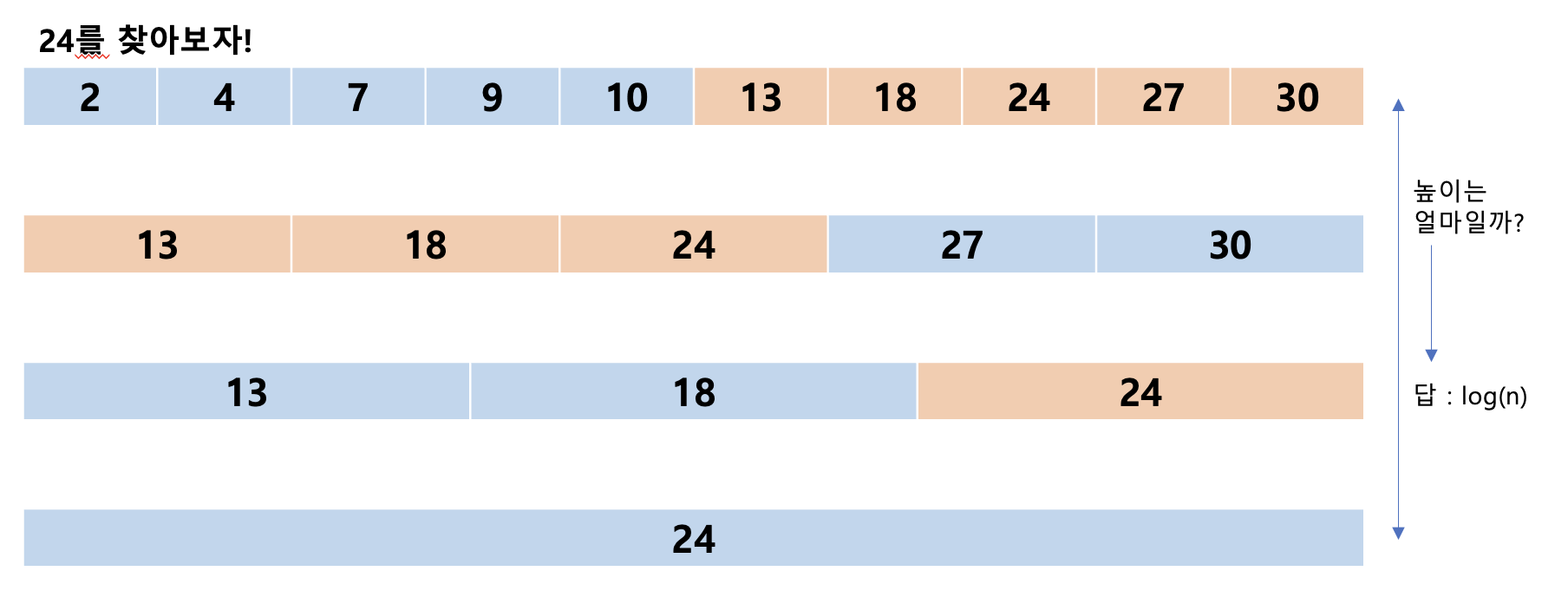
장점 : 순차 탐색으로 n이 존재하는지 확인하기 위해서는 최악의 경우 n칸을 모두 순회하며 찾아야 하므로 순차 탐색의 시간 복잡도는 O(n)이다 그러나 이분 탐색은 절반씩 나누며 필요 없는 부분은 순회하지 않는다 따라서 위 그림의 높이처럼 시간 복잡도는 O(log(n))이 된다!

단점 : 순차 탐색은 정렬되지 않은 데이터에서도 값을 찾을 수 있지만 이진 탐색은 항상 정렬된 데이터에서만 탐색이 가능하다.

합병 정렬(Merge Sort)

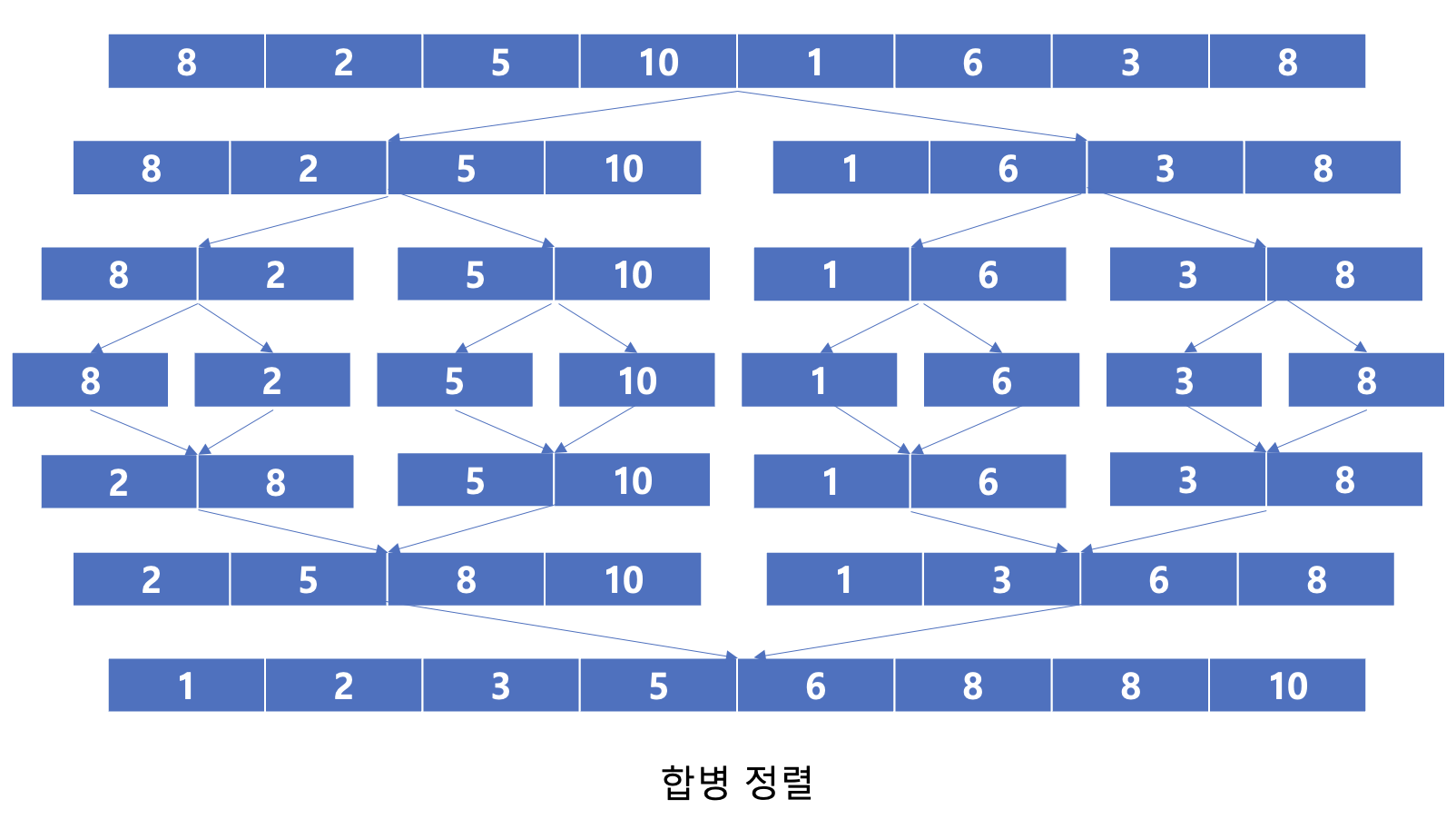
시간 복잡도 nlog(n)
공간복잡도 2n