Tree

정의

노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조

Tree의 구성 요소

루트 노드 : 트리 구조의 최상위의 있는 노드

부모 노드 : 트리 계층 관계에서 상위에 있는 노드

자식 노드 : 트리 계층 관계에서 하위에 있는 노드

형제 노드 : 같은 부모들 가지는 노드

비단말 노드 : 자식 노드가 있는 노드

단말 노드(리프 노드) : 자식 노드가 없는 최하위 노드

깊이 : 어떤 노드에서 루트 노드까지 가장 긴 경로의 간선 수

높이 : 어떤 노드에서 단말 노드까지 가장 긴 경로의 간선 수

레벨 : 루트 노드로부터 임의의 노드까지의 깊이 (root = 1)

차수 : 노드가 가지는 자식의 수

지름 : 가장 거리가 먼 두 노드간의 거리

Tree의 종류

이진 트리 : 최대 자식의 수가 2개인 트리

균형 트리 : 모든 리프 노드의 차수가 1 이하의 차이를 갖는 트리

완전 트리 : 리프 노드를 제외한 모든 노드가 포화 상태인 트리

알고리즘에서 자주 사용되는 이진 트리의 특징

높이가 h인 이진 트리의 경우, 최소 h개의 노드를 가지며 최대 2^h - 1개의 노드를 가진다. (포화 이진 트리의 노드의 수 2^h - 1)

포화 이진 트리에서 배열 표기법 (root의 idx = 1)

노드 i의 부모 노드 idx = i/2

노드 i의 왼쪽 자식 idx = 2i

노드 i의 오른쪽 자식 idx = 2i+1

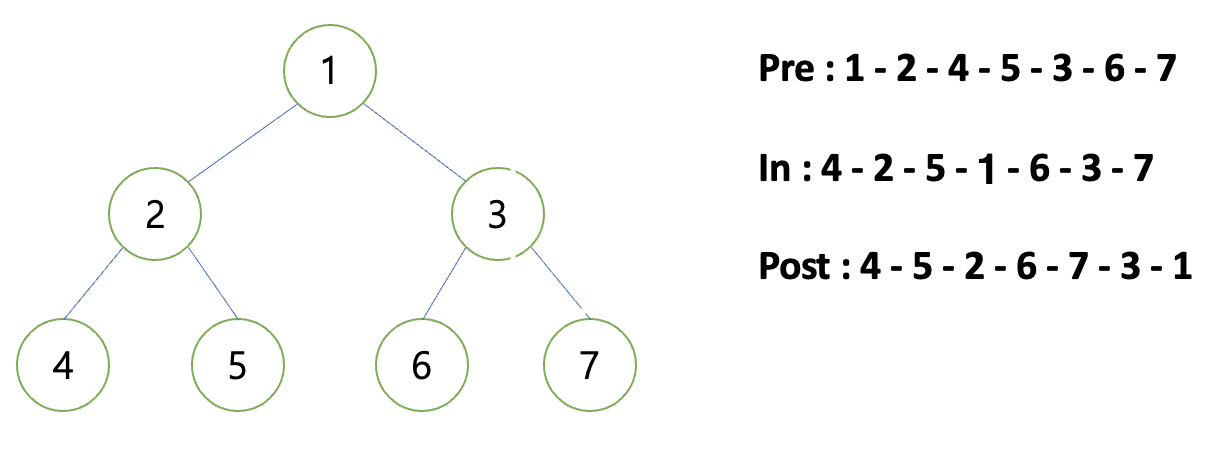
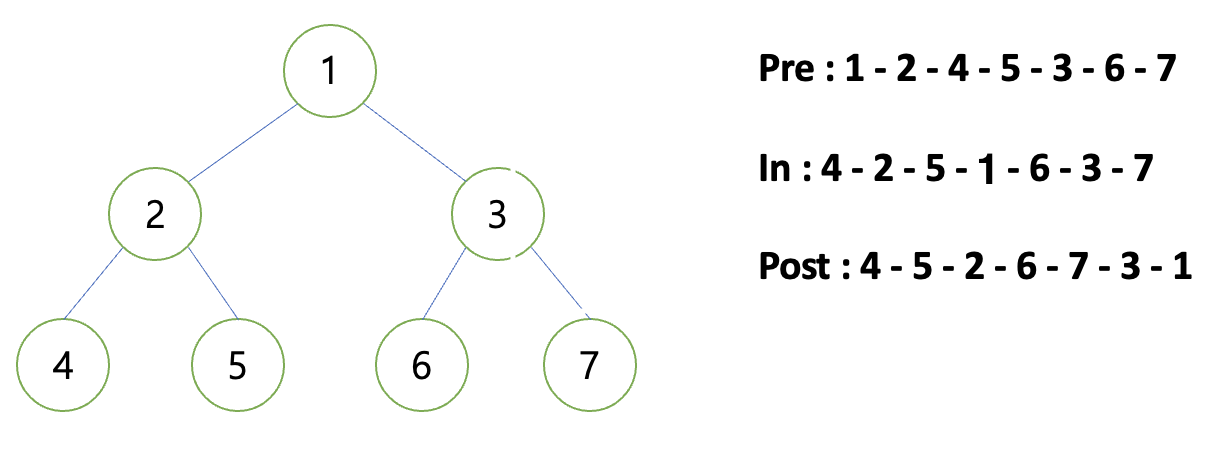
이진 트리의 탐색

전위 순회(Preorder) : 부모를 먼저 방문하는 순회 방식

부모 노드 > 왼쪽 노드 > 오른쪽 노드

중위 순회(Inorder) : 왼쪽 노드를 먼저 방문하는 순회 방식

왼쪽 노드 > 부모 노드 > 오른쪽 노드

후위 순회(Postorder) : 부모 노드를 마지막에 방문하는 순회 방식

왼쪽 노드 > 오른쪽 노드 > 부모 노드

void Pre(char n) {
  cout << n;
  if(L[n] != '.') Pre(L[n]);
  if(R[n] != '.') Pre(R[n]);
}

void In(char n) {
  if(L[n] != '.') In(L[n]);
  cout << n;
  if(R[n] != '.') In(R[n]);
}

void Post(char n) {
  if(L[n] != '.') Post(L[n]);
  if(R[n] != '.') Post(R[n]);
  cout << n;
}