[U_stage] - week1

[Day1] 2021/08/02

강의 리뷰

-AI Math 1강: 벡터가 뭐예요?

• 벡터란 숫자를 원소로 가지는 리스트(list)또는 배열을 지칭합니다.
• 벡터는 공간(1,2,3,..차원)에서 한점을 나타내며, 원점으로부터의 위치를 표현합니다.
• 같은 모양일 경우, 덧셈,뺄셈과 성분곱이 가능합니다.
• 벡터의 노름은 원점으로부터의 거리를 말합니다.
  $ex) l1노름:\parallel x \parallel _1 ,ㅣ2노름: \parallel x \parallel _2$
• 각각은 변화량의 절대값과 유클리드 거리를 의미합니다.
• 두 벡터 사이의 거리는 벡터의 뺄셈을 이용합니다.

  

• 위는 두 벡터 사이의 각을 구하는 공식입니다.

-AI Math 2강: 행렬이 뭐예요?

• 행렬(matrix)는 벡터를 원소로 가지는 2차원 배열입니다.
• 행렬은 행(row)과 열(column)이라는 인덱스를 가집니다.
• 벡터는 한점을 행렬은 여러 점들을 나타냅니다.
• 같은 모양을 가진 행렬은 덤셈, 뺄셈, 성분곱을 할 수 있습니다.
• 어떤 행렬에 곱하여 항등행렬로 만들 수 있는 행렬을 역행렬이라고 합니다.
• 이런 행렬의 특징을 살려 선형 회귀 분석을 할 수 있습니다.
  

과제

1. Basic Math: 기본 연산 문제
2. Text Processing 1: join함수와 split함수를 이용한 문자열 다루기
3. Text Processing 2: join함수와 split함수를 이용한 문자열 다루기
4. 벡터, 행렬, 경사하강법관련 개념 퀴즈

피어세션

첫 피어세션이라서 Ice-breaking하는 시간일 줄 알았는데, 다른 팀원분들이 모두 학업에 열정적이신 것 같아 솔직히 부담스러웠다. 하하...

• 팀명, 그라운드룰, 모더레이터 정하기

마무리

쉬웠다고 할 수 없는 과정을 거쳐서 참여할 수 있었다. 솔직히 인공지능 관련 전공자이지만 부족하다는 것을 스스로 알았습니다. 게을렀던 것도 맞고 방향성도 딱히 없었지만 이번 기회에 찾길 바라봅니다..
첫 피어세션을 통해서 열심히 하고 싶다느 동기가 생겼습니다. 모든 팀원분들이 굉장히 열정적이셨고 다들 수준급으로 잘하시는 느낌인데 서로 상부상조하며 성장하고 싶습니다.
노는 걸 워낙 좋아하지만 이번 5개월은 열정적으로 해보고싶습니다. 화..이팅 ^_^

[Day2] 2021/08/03

강의 리뷰

-AI Math 3,4강: 경사하강법(순한맛,매운맛)

미분(differentiation)과 경사하강법:

• 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구, 최적에 제일 많이 쓰입니다.
  

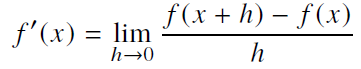
• 함수 f의 한 점 (f,f(x))에서의 접선의 기울기로, 방향에 따라 함수값의 증/감을 알 수 있습니다.

• 미분값을 더하고 뺌에 따라 경사상승법과 경사하강법으로 나뉘며, 극대값과 극소값의 위치를 구할 수 있습니다. 그리고 이 두 방법은 극값에 도달하면 움직임(업데이트)을 멈춥니다.

• 경사하강법 알고리즘:

  Input: gradient(미분 계산 함수), init(시작점), lr(학습률), eps(알고리즘 종료조건)
  Output: var
  
  var = init
  grad = gradient(var)
  while( abs(grad) > eps ):
      var = var - lr * grad
      grad = gradient(var)

변수가 벡터라면?

• 벡터가 입력인 다변수 함수의 경우 편미분(partial differentiation)을 사용합니다.
• 각 변수 별로 편미분을 계산한 그레디언트(gradient) 벡터를 이용하여 경사하강/경사상승법에 사용할 수 있습니다.
• 기본 알고리즘은 위와 같으나, 절대값 대신 노름(norm)을 계산해야 합니다.

    while( norm(grad) > eps ):

경사하강법을 이용한 선형회귀:

+ 위는 선형회귀의 목적식이고, 이를 최소화하는 β를 찾아야 합니다.

• 선형회귀의 목적식을 최소화 하는 β를 구하는 경사하강법의 알고리즘은 위와 같습니다.

  Input: X, y, lr, T,
  Output: beta
  
  for t in range(T):
   error = y - X @ beta
   grad = - transpose(X) @ error
   beta = beta - lr * grad

• (이론적으로) 경사하강법은 미분가능하고 볼록(convex)한 함수에 대해선 적절한 학습률과 학습횟수를 선택했을때 수렴이 보장되어 있으며, 볼록한 함수는 그레디언트 벡터가 항상 최소점을 향합니다.

• 하지만, 비선형회귀의 문제인 경우 목적식이 볼록하지않을 수 있기 때문에 수렴이 보장되지는 않습니다. 특히, 아쉽게도 딥러닝의 경우 목적식이 대부분은 볼록함수가 아닙니다.

확률적 경사하강법(SGD,stochastic gradient descent):

• 모든 데이터가 아닌 한개 또는 일부 데이터의 그레디언트를 계산후 업데이트하는 방식이다.
• 한개가 아닌 일부인 경우 mini-batch SGD라고 한다.
• 만능은 아니지만, 딥러닝에선 경사하강법보다 실증적으로 더 낫다고 검증되어 있습니다.

  

• SGD는 위와 같은 미니배치를 가지고 그레디언트 벡터를 계산합니다. 미니배치는 확률적으로 선택하므로 목적식 모양이 매번 다릅니다.
• 볼록이 아닌 함수라고 하더라도 SGD를 활용하여 최소점을 찾을 수 있다.

과제

1. Baseball: 반복문, 문자열비교를 이용한 알고리즘
2. Morsecode: 문자열 관련 함수를 이용한 간단한 알고리즘 문제들
3. 딥러닝 학습방법및 확률론 관련 퀴즈

  #딕셔너리의 key와 value를 바꾸는 방법
  reversed_morse_code_dict = dict(map(reversed,morse_code_dict.items()))

피어세션

• [8/4 피어세션이 피었습니다] 계획
• 파이썬, 넘파이, 판다스 관련 강의 리뷰

마무리

어제의 피어세션은 ice-breaking의 시간을 가졌다면, 오늘은 다른 팀원분이 준비하신 강의 리뷰를 통해서 피어세션의 효과를 보았습니다. 알고있는 내용일지라도 복습하고 한 층 더 익숙해졌습니다.
어제보다 조금은 긴장이 완화되어서 다행입니다 ^ㅡ^

[Day3]2021/08/04

강의 리뷰

-AI Math 5강: 딥러닝 학습방법 이해하기

• 신경모델은 대부분은 선형모델을 기반으로 한 비선형입니다.

  

  

• 위 그림에서 화살표는 각각의 가중치W를 의미합니다.

• Softmax함수는 모델의 출력을 확률로 해석할 수 있도록합니다.

  

• 분류문제를 풀때 선형모델과 sofrtmax함수의 결합으로 예측합니다.

• 학습하는 경우는 Softmax함수가 쓰지만, 추론할 경우에는 사용하지 않습니다.

• 신경망은 선형모델과 활성함수를(activation function)를 합성한 함수입니다.

• 활성함수는 R위에 정의된 비선형함수로서 딥러닝에서 매우 중요한 개념입니다.

  

• 예전에는 Sigmoid함수와 tanh함수를 많이 썼지만, 근래에는 Relu함수를 쓴다.

  

• 위 그림은 다층퍼셉트론(MLP)을 표현합니다. x를 입력으로 받아 W1가중치 행렬을 통해 z로 보내고 활성함수를 통해서 H행렬을 구하고, 이 메커니즘을 다층으로 구성합니다.그리고 이 과정을 순전파(forward propagation)라고 한다.

• 층이 깊을수록 목점함수를 근사하는데 필요한 뉴런(노드)의 숫자가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능합니다.

• 딥러닝은 역전파(back propagation)알고리즘으로 각층에서 사용된 파라미터(W,b)를 학습합니다.(역순으로)

• 역전파 알고리즘은 합성함수 미분법인 연쇄법칙(chain-rule)기반 자동미분(auto-differentiation)을 사용합니다.
  

-AI Math 6강: 확률론 맛보기

• 데이터 공간을 x * y라고 표기하고 D는 데이터공간에서 데이터를 추출하는 분포입니다.
• 데이터는 확률변수로 (x,y)~D라 표기합니다.
• 확률변수는 확률분포 D에 따라 이산형(discrete)과 연속형(continuous) 확률변수로 구분하게 됩니다.
• 이산형 확률 변수는 확률 변수가 가질 수 있는 경우의 수를 모두 교려하여 확률을 더해서 모델링합니다. 반면, 연속형 확률변수는 데이터 공간에 정의된 확률변수의 밀도(density)위에서의 적분을 통해 모델링합니다.
• 결합분포 P(x,y)는 D를 모델링합니다.
• 조건부확률분포 P(x|y)는 데이터 공간에서 입력x와 출력 y의 관계를 말합니다.
• 조건부확률P(y|x)는 입력변수x에 대해 정답이 y일 확률을 의미합니다.
• 로지스틱 회귀에서 사용했던 선형모델과 소프트맥스 함수의 결합은 데이터에서 추출된 패턴을 기반으로 확률을 해석하는데 사용됩니다.
• 기대값(expectation)은 데이터를 대표하는 통계랑이면서 동시에 확률분포를 통해 다른 통계적 범함수(분산,첨도,공분산 등)을 계산할 수 있습니다.
• 딥러닝은 다층신경망을 사용하여 데이터로부터 특징패선을 추출합니다.
• 기계학습의 많은 문제들은 확률분포를 명시적으로 모를 때가 대부분이고, 데이터를 이용하여 기대값을 계산하려면 몬테카를로(Monte Carlo)샘플링 방법을 사용해야 합니다. 이 방법은 독립추출만 보장된다면 대수의 법칙에 의해 수렴성을 보장합니다.
  

-AI Math 7강: 통계학 맛보기

• 통계적 모델링의 목표는 적절한 가정 위에서 확률분포를 추정하는 것입니다. 그러나 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 아는 것은 불가능하므로, 근사적으로 확률분포를 추정할 수 밖에 없습니다.
• 가정후 분포를 결정하는 모수를 추정하는 방법을 모수적(parametric) 방법론이라고 합니다. 대부분의 기계학습은 특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌는 비모수 방법론을 이용합니다.
• 히스토그램을 통해 모양 관찰하여 확률분포를 베르누이 분포, 카테고리분포, 베타분포,감마분포, 로그정규분포, 정규분포 또는 라플라스분포 등으로 볼 수 있습니다. 하지만 가정시에 제일 중요한 것은 데이터를 생성하는 원리입니다.
• 정규분포의 모수는 평균과 분산이 있습니다.
• 통계량의 확률분포를 표집분포라 합니다.
• 가장 가증성이 높은 모수 추정 방법 중 하나는 최대가능도 추정법(Maximum Likelihood Estimation,MLE)입니다.
  

과제

• 선택과제로 경사하강법 구현을 해봤습니다. 이론을 잘 적용시켰더니 어렵지않게 구현할 수 있었습니다. 특히 강의에 나왔던 알고리즘(경사하강법 강의 리뷰에 작성한 코드와 동일)을 적용했습니다.
• 통계학, 베이즈통계학, CNN 관련 퀴즈

피어세션

• 선형대수, 확률 및 통계 강의 리뷰
  

마무리

이벤트 [피어세션이 피어씁니다]를 통해서 다른 분들과 인사할 수 있는 기회가 되었고, 제가 발표자로 우리 조를 소개하는 시간도 가졌습니다. 모든 분들이 열정적이신 것 같다는 것에 또 한번 동기 부여를 받았습니다.
내일 있을 마스터 클래스와 첫 멘토링 시간이 매우 기대됩니다.^_^

[Day4] 2021/08/05

강의리뷰

-AI Math 8강: 베이즈 통계학 맛보기

• 조건부 확률

  

  

• 조건부 확률의 시각화 (예)

  

• 베이즈 정리를 통해 새로운 데이터가 들어왔을때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있습니다.
• 조건부확률은 유용한 통계적 해석을 제공하지만 인과관계 추론에는 사용할 수 없다.
• 인과관계는 데이터 분포의 변화에 강건한 예측모형을 만들 때 필요합니다.
• 인과관계를 알아내기 위해서는 중첩요인(confoundging factor)의 효과를 제거하고 원인에 해간하는 변수만의 인과관계를 계산해야 합니다.

-AI Math 9강: CNN 첫걸음

• 이전까지의 다층신경망(MLP)은 각 뉴런들이 선형모델과 활성함수로 모두 연결된(fully-connected) 구조였습니다. 하지만, 각성분 h(i)에 대응하는 가중치 행 W(i)이 필요합니다.(학습해야하는 파라미터가 커짐)
• convolution연산은 커널(kernel)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조입니다.

  

  

• Convolution 연산의 수학적인 의미는 신호(signal)를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출또는 필터링하는 것입니다.

  

• 커널은 정의역 내에서 움직여고 변하지 않고 주어진 신호에 국소적으로 적용합니다.
• Convolution은 1차원뿐만 아니라 다양한 차원에서 계산가능합니다.
• 2D-Conv 연산은 커널(kernel)을 입력벡터상에서 움직여가면서 선형모델과 합성함수가 저굥되는 구조입니다.
• 입력 크기를 (H,W), 커널크기를 (KH,KW),출력크기를 (OH,OW)라 하면 출력크기는 OH = H - KH + 1 , OW = W - KW + 1 입니다.
• 채널이 여러개인 2차원 입력의 경우 2차원 Convolution을 채널개수만큼의 커널로 적용합니다.
• convolution의 역전파를 계산할때도 convolution연산이 나오게 됩니다.

  

과제

RNN관련 퀴즈
: BPTT관련 확장 개념을 조금 더 공부할 필요성을 느낌.

피어세션

• 경사하강법(본인), CNN 강의 리뷰
• 차주 피어세션부터 시작할 스터디 선택 토의(캐글/논문리뷰)

마무리

• 마스터클래스: 수학의 기초를 잘 만들어 놓으면 논문 구현에 큰 도움이 된다. (선형대수, 확률, 통계)

• 첫번째 멘토링:

  • 피어세션 스터디로 캐글과 논문중 캐글 추천
  • CV(한,영버전)를 꾸준히 미리 준비
  • 꾸준한 코딩테스트 준비(파이썬 알고리즘 인터뷰 도서 추천)
  • Transformer(Attention is all you need) 읽기

  오늘 첫 마스터 클래스와 멘토링 시간을 통해서 준비해야 할 것들이 너어어어무 많다는 것을 다시 한번 알게되었습니다. 다음주부터 점점 더 어려워지더라도 쫄지 않겠습니다.^_^

[Day5] 2021/08/06

강의리뷰

-AI Math 10강: RNN 첫걸음

• 순차적으로 들어오는 시퀀스 데이터의 예로는 소리, 문자열(문장의도,문맥), 주가 등이 있다.
• 시퀀스 데이터는 독립동등분포(i,i,d) 가정을 잘 위배하기 때문에 순서를 바꾸거나 과거 정보에 손실이 발생하면 데이터의 확률분포도 바뀌게 됩니다. 과거 정보 또는 앞뒤 맥락없이 미래를 예측하거나 문장을 완성하는건 불가능.
• 시퀀스 데이터는 조건부 확률을 이용할 수 있다. 하지만 과거의 모든 정보들이 꼭 필요한 것만은 아닙니다.

  

• 시퀀스 데이터를 다룰때는 길이가 가변적인 데이터 모델이 필요합니다.
• 고정된 길이τ만큼의 시퀀스만 사용하는 경우 AR(τ)(Autoregressive Model) 자기회귀모델이라고 부릅니다.
• 또다른 방법은 바로 이전 정보를 제외한 나머지 정보들을 Ht라는 잠재변수로 인코딩해서 활용하는 잠재AR모델입니다.
• 잠재변수Ht를 신경망을 통해 반복해서 사용하여 시퀀스 데이터의 패턴을 학습하는 모델이 RNN입니다.

  

• 위 그림처럼 Ht를 복제해 다음 순서의 잠재변수를 인코딩하는데 사용합니다.
• Backpropagation Through Time(BPTT)는 RNN의 역전파 방법이다.
• 시퀀스 길이가 길어지는 경우 BPTT를 통한 역전파 알고리즘의 계산이 불안정해지므로 길이를 끊는 것이 필요합니다.

과제

오피스아워전에 이전까지의 문제들을 다시 한번 훑어보며 과제들을 상기시키며 내 것을 만드는 시간을 가졌습니다.

피어세션

• 포켓몬 데이터 또는 손글씨데이터로 다음주부터 분류해보기
• 벡준그룹을 이용한 코딩공부 함께 시작

마무리

오피스아워를 통해서 필수과제와 선택과제에 대한 가이딩을 받아서 주말동안 나머지 선택과제를 혼자서 풀어볼 예정입니다.
한 주동안 워밍업 하자라는 생각을 했지만 생각보다 시간 소요가 많았습니다. 기초를 더 탄탄히 해야겠다는 다짐이 섰습니다. 피곤한 한 주였지만 신기하게도 재밌었습니다. 본격적인 협업이 시작되는 것에 흥미를 느끼고 있습니다. 다음주도 열정을 다하자라는 마음가짐으로 참여할 것입니다.