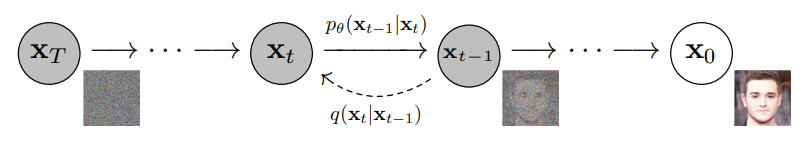1. 주요 아이디어
diffusion 모델은 점진적 변환을 통해 노이즈를 추가하고, 반대로 노이즈를 제거하는 과정을 통해 원래 데이터를 복원하는 원리를 사용. 이 과정은 두 단계로 나눠짐.
- Forward Process : 원본 데이터에 점진적으로 노이즈를 추가하여, 점차적으로 무작위 노이즈로 변환
- Reverse Process : 노이즈가 추가된 데이터에서 점진적으로 노이즈를 제거하여, 원본 데이터를 복원
1-1 Diffusion 의미
diffusion은 확산 현상을 의미
이 때, 분자의 움직은 가우시안 분포를 따름 -> 평균 𝜇과 표준 편차 𝜎를 따르는 정규 분포로 움직임을 표현이 가능
=> 매 시간 t마다 각 분자의 움직을 계산해낼 수 있다면 diffusion을 반대로 진행하여 원본 상태로 복구 가능
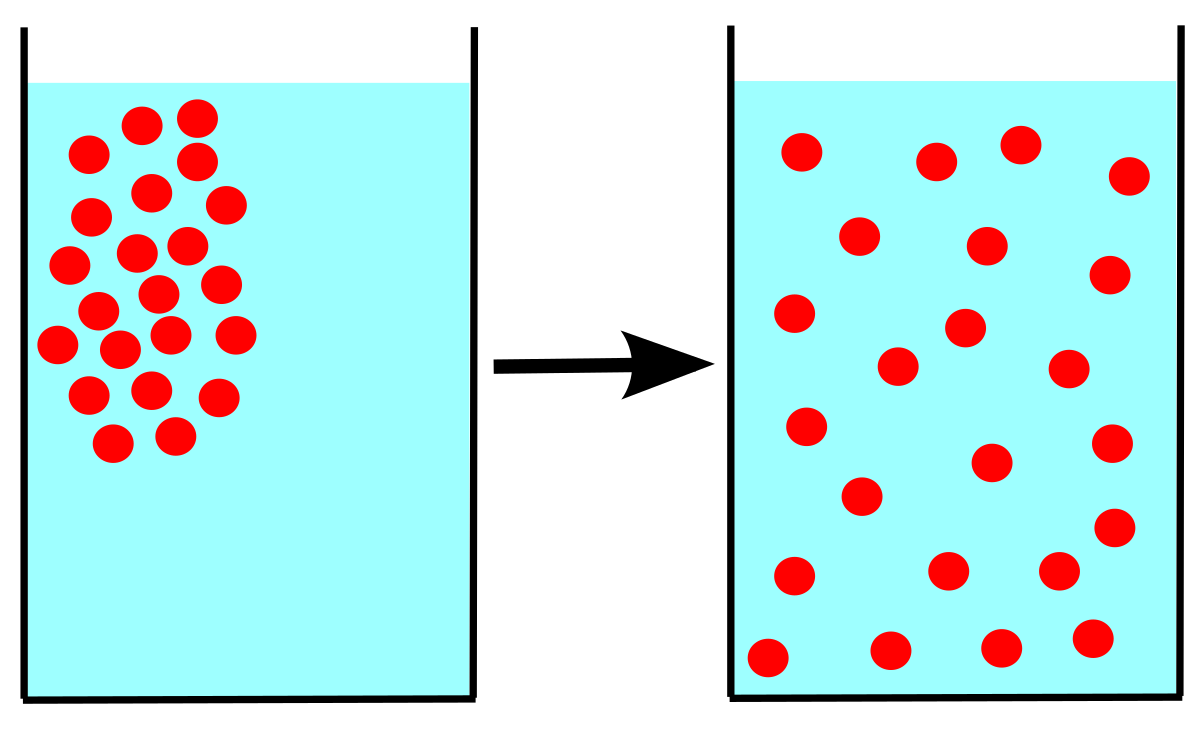
이러한 아이디어로 Image의 pixel 값에 적용하여 학습에 적용
2. Forward Process
Forward Process에서는 데이터 x0에 작은 노이즈를 단계적으로 추가하여 𝑥1,𝑥2,…,𝑥𝑇와 같은 일련의 변환된 데이터 시퀀스를 생성, 이 과정은 각 단계에서 일정한 분포를 따라 노이즈를 추가하는 방식으로 이루어짐.
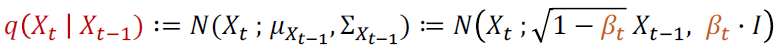
여기서 Bt는 각 단계에서 노이즈의 크기를 조절하는 하이퍼 파라미터
3. Reverse Process
Reverse Process에서는 Forward Process에서 생성된 노이즈 데이터를 역으로 변환하여 원래 데이터를 복원. 이는 조건부 확률 p(xt−1∣xt)을 학습하는 방식으로 이루어지며, 일반적으로 신경망을 사용하여 이 확률 분포를 모델링.
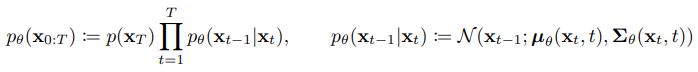
위 식에서, 각 단계의 정규 분포의 평균 uθ 표준편차 Σθ는 학습되어야 하는 파라미터
그리고 시작지점인 노이즈의 분포는 표준정규분포로 정의
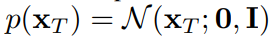
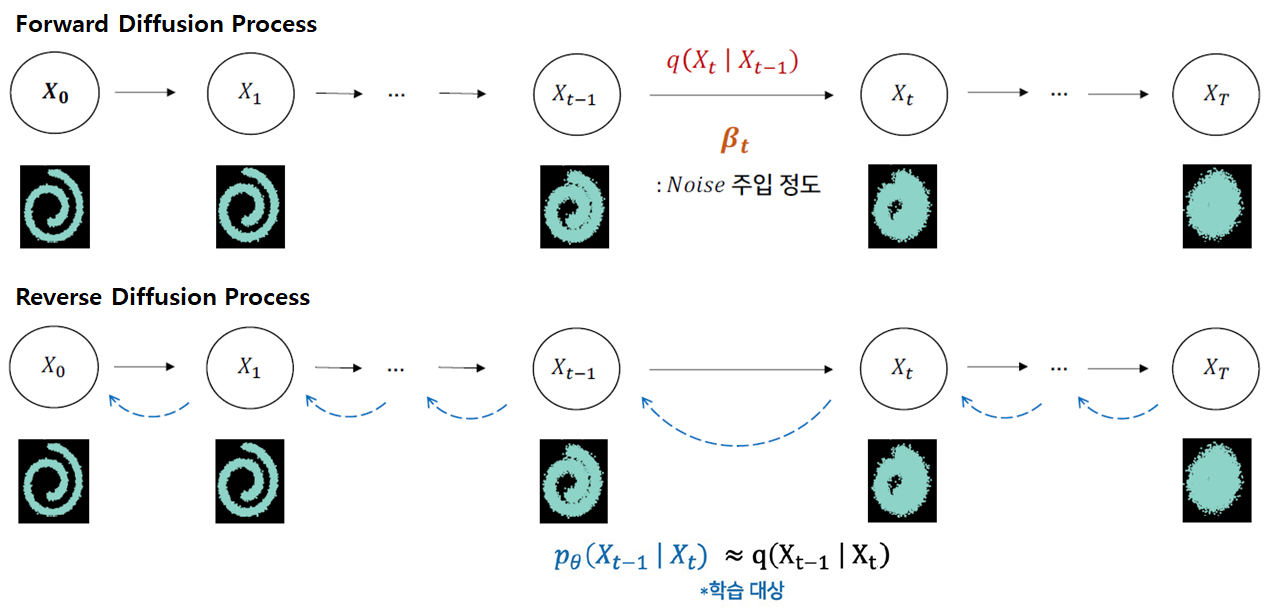
=> diffusion 모델의 학습은 forward process와 reverse process의 확률 분포 간의 차이를 최소화하는 방식으로 이루어짐.
확률분포 q에서 관측한 값으로 확률 분포 pθ의 likelihood를 구하였을 때, 그 likelihood값이 최대(Maximum)가 되는 확률분포를 찾는 Maximum Likelihood Estimation 문제
4. 수식으로 이해해보기
알아둬야 할 사전 지식
1. 베이지안 룰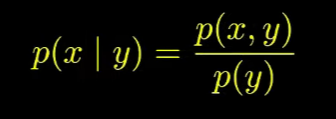
2. markov chain 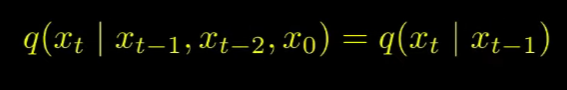
diffusion 모델의 training loss
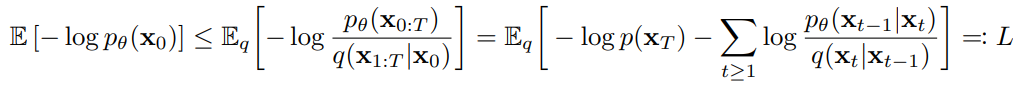
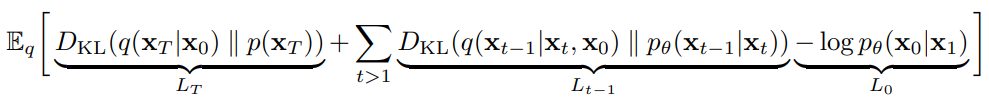
LT : p 가 generate하는 noise Xt와 q가 X0라는 데이터가 주어졌을 때 genrate하는 noise Xt간의 분포 차이
Lt-1 : p와 q의 reverse/forward process의 분포 차이 이들을 최대한 비슷한 방향으로 학습
L0 : latent x1 으로부터 data x0를 추정하는 likeihood 이를 maximize하는 방향으로 학습
[reference]
https://process-mining.tistory.com/182
https://ffighting.net/deep-learning-paper-review/diffusion-model/diffusion-model-basic/
https://www.youtube.com/watch?v=ybvJbvllgJk