[백준] 23578. 비 오는 날

문제 링크

1. 문제 설명

피에스고등학교의 교장 이환이는 학교를 매우 사랑한다. 그래서 이환이는 매일 점심시간에 학교의 모든 건물을 돌아다닌다. 비가 오는 어느 날, 이환이는 학교 곳곳을 돌아다니고 싶었지만 비를 끔찍이 싫어하기 때문에 그럴 수 없었다.

비 때문에 고민하던 이환이는 결국 비를 맞지 않고 학교의 모든 건물을 방문할 수 있도록 건물과 건물 사이에 구름다리를 설치하기로 했다. 하지만 학생들은 비가 오는 날마저 이환이가 돌아다니면 게임을 하다 걸릴까 봐 구름다리 설치를 반대했다. 건물 $i$
와 다른 건물을 잇는 구름다리가 $k$개 설치되면, 건물 $i$에서 게임을 하던 학생들은 $k$개의 구름다리에서 이환이가 오는지 확인해야 하기 때문에 $k^2$만큼의 불만을 가진다.

점심시간에 건물 1에는 학생 1명, 건물 2에는 학생 2명, 건물 3에는 학생 3명이 게임한다고 가정하자. 아래와 같이 구름다리를 건설하면 건물 2와 건물 3에 있는 학생들은 불만을 1씩 가지고 건물 1에 있는 학생은 불만을 4 가진다. 따라서 이때 생기는 학생들의 불만은 $1×4+2×1+3×1=9$이다. 불만이 9보다 작도록 구름다리를 건설하는 것은 불가능하다.

실제로 피에스고등학교에는 $N$개의 건물이 있고, $i$번 건물에서는 $ai$명의 학생이 게임을 한다. 학생의 불만이 크면 이환이가 상처받기 때문에, 이환이를 위해 불만의 최솟값을 구해줘야 한다.

• 입력
  첫 번째 줄에 건물의 수 $N$이 주어진다.

  두 번째 줄에는 각 건물에서 게임을 하는 학생의 수를 나타내는 음이 아닌 정수 $a_1,a_2,⋯,a_N$이 공백으로 구분되어 주어진다.

• 출력
  첫 번째 줄에 불만의 최솟값을 출력한다.

2. 문제 접근

불만의 값을 최소로 하면서 모든 건물을 연결을 하고자 합니다. 언뜻 보기엔 MST 문제 같지만, 불만을 산출하는 과정이 단순 간선의 건물(노드)가 가진 값의 합의 누적이 아니기 때문에 그런 방식으로 구할 수 없습니다. 애초에 MST 알고리즘대로 하면 가장 값이 적은 건물에 모든 건물을 연결하는 깊이 1의 트리 같은 구조가 될텐데, 당연히 그렇게는 답을 구할 수 없습니다.

따라서 이번 문제에서는 그래프를 차수열(Degree Sequence)로 표현해 보겠습니다. 차수열의 개념은 간단합니다. 각 노드의 차수를 단순히 나열한 수열입니다.

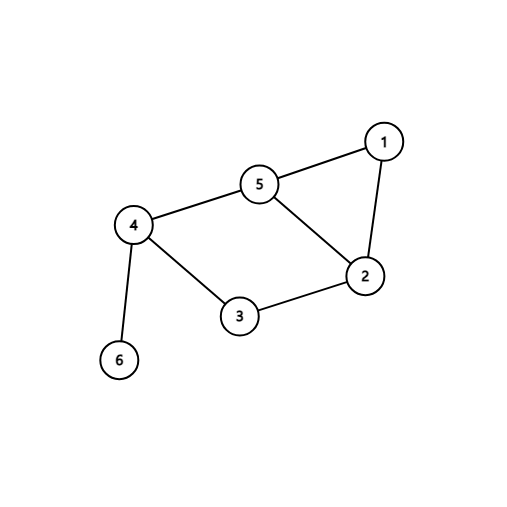
위 그래프의 차수를 1부터 6까지 나타내면 [2, 3, 2, 3, 3, 1] 입니다.

차수열의 유효성을 확인할 수 있는 특징이 몇 가지 있습니다. 첫 번째로 수열의 합은 반드시 짝수여야 합니다. 간선 하나당 차수가 2씩 올라가서 그렇습니다. 또한 같은 차수열를 나타내는 그림이 하나 이상 있을 수 있습니다.

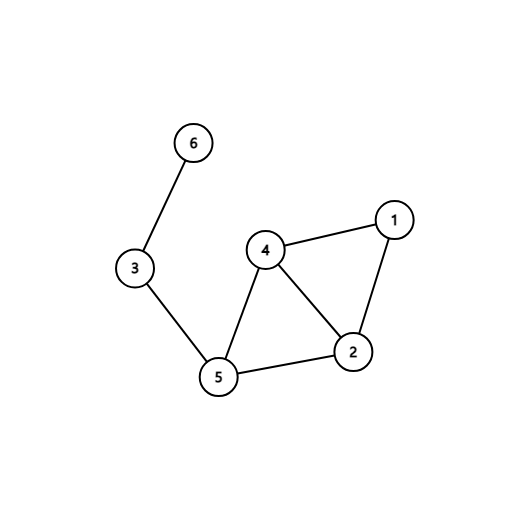
같은 차수열을 공유하는 전혀 다른 그래프입니다.

차수열의 유효성을 확인하는 가장 강력한 정리는 하벨-하키미 정리(Havel-Hakimi Theorem)입니다. 차수열를 내림차순 정렬한 뒤, 차수가 가장 큰 노드를 하나 제거하고 그 노드의 차수의 개수만큼 다음으로 큰 노드들의 차수를 1씩 빼주는 과정을 반복합니다. 그 과정에서 생성되는 모든 새로운 차수열이 그래프로 표현 가능하다면 유효한 차수열입니다.

자세한 증명은 어려우니 위 그래프에 적용을 해보겠습니다.
1. 차수열을 정렬하면 [3,3,3,2,2,1]이 됩니다. 노드 번호는 [2,4,5,1,3,6]이라 합시다.
2. 첫 번째 노드를 제거합니다. 차수가 3인 2번 노드를 제거하는데, 편의를 위해 다음으로 차수가 큰 3개 노드인 4, 5, 1번에 연결되어 있다고 가정합니다.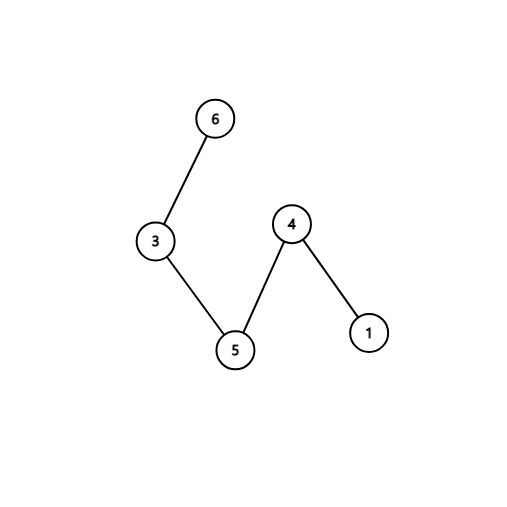
3. 수열은 [2, 2, 1, 2, 1], 노드 번호는 [4,5,1,3,6]이 됩니다. 이는 위 그래프와 같으며, 같은 방법으로 노드를 하나씩 제거할 수 있습니다.

같은 방법으로 [3, 3, 3, 1] 이 유효하지 않은 차수열임을 보일 수 있습니다.
1. [3, 3, 3, 1]에서 첫 번째 항을 제거합니다. 이후 차수열은 [3-1, 3-1, 1-1] = [2, 2, 0] 이 됩니다.
2. [2, 2, 0]은 그래프로 나타낼 수 없습니다. 그림을 그려 보려 시도해 보면 알 수 있습니다.

문제에서 찾는 그래프는 트리인데 다행히 트리에서는 위와 같은 유효성 확인 과정이 필요 없습니다. 총 노드가 $n$개면,
1. 차수열의 총 합이 $2n - 2$ 이고,
2. 모든 노드의 최소 degree가 1이며,
3. 모든 노드의 최대 degree가 n - 1이여야 합니다.

노드의 값이 $k$, 차수가 $d$일 때 차수가 1 증가할 때 증가하는 불만의 값은 $k*(2d+1)$입니다. 따라서 매번 증가하는 불만이 가장 적은 노드의 차수를 1 증가싴키고, 다음 증가하는 불만의 값을 $k*(2d+3)$으로 업데이트 해줍니다. 차수가 $d+1$이고 한번 더 증가할 때는 $d+2$가 되기 때문입니다. 이는 PriorityQueue를 사용해 구현할 수 있습니다.

3. 문제 풀이

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

public class Main {

    static class Node implements Comparable<Node> {
        long num, degree;

        public Node(long num, long degree) {
            this.num = num;
            this.degree = degree;
        }

        public int compareTo(Node o) {
        	if (this.num > o.num) return 1;
        	else return -1;
        }
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        long ans = 0;
        PriorityQueue<Node> queue = new PriorityQueue<>();

        Node[] graph = new Node[n];
        StringTokenizer st = new StringTokenizer(br.readLine());
        
        for (int i = 0; i < n; i++) {
            long a = Long.parseLong(st.nextToken());
            graph[i] = new Node(a, 1);
            queue.offer(new Node((graph[i].degree * 2 + 1) * graph[i].num, i));
        }

        if (n == 1) {
            System.out.println(0);
            System.exit(0);
        }

        for (int i = 1; i < n - 1; i++) {
            Node cur = queue.poll();
            graph[(int) cur.degree].degree++;
            queue.offer(new Node((graph[(int) cur.degree].degree * 2 + 1) * graph[(int) cur.degree].num, cur.degree));
        }

        for (int i = 0; i < n; i++) ans += graph[i].num * graph[i].degree * graph[i].degree;     

        System.out.println(ans);
    }

}