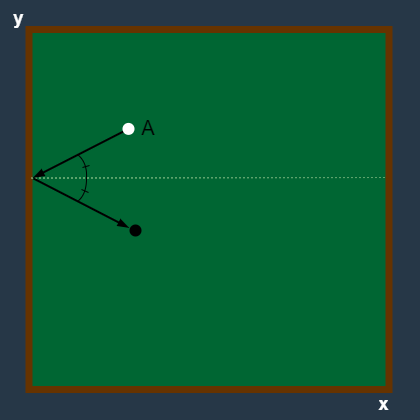
1. 문제 설명
요약하자면, 당구공을 시작 위치에서 목표 위치까지 당구공이 움직이는 최소 거리를 구해야 합니다. 당구공은 반드시 당구대 한 면을 '원쿠션' 해야 하며, '원쿠션' 전에 당구공이 목표 위치에 도달한다면 이는 올바른 루트가 아니게 됩니다.
2. 문제 접근
문제 해결을 위한 기본 개념은 중고등학교 수학에서 배웠던 선대칭이동입니다. 당구대를 (m , n) 크기의 좌표평면으로 놓고, 시작 위치와 목표 위치의 x, y축 좌표를 놓고 나면 굉장히 쉬운 수학 문제가 됩니다! 블로깅을 위해 구글링을 하다가 고1수학 최단거리 문제를 친절하게 설명해주신 블로그를 찾았으니 링크하겠습니다. (링크) 옛날 생각 나고 좋네요.. ㅎㅎ
문제는 당구대의 네 변 중 어떤 변으로 대칭 이동을 해야 최단 거리가 되는지 찾는 것입니다. 처음에는 네 가지 경우의 이동 거리를 모두 구해서 단순 비교하는 접근 방식을 생각했습니다.
def solution(m, n, startX, startY, balls):
answer=[]
for ball in balls:
x, y = ball[0], ball[1]
answer.append(min(((startX-x)**2+min((startY+y),(2*n-startY-y))**2),((startY-y)**2+min((startX+x),(2*m-startX-x)))**2))
return answer당구공이 당구대의 세로 변, 즉 x=0 또는 x=m 에 대해 대칭이동 할 때 두 점이 x=0과 x=m 중 어느 축에 가까운지 판단하기 위해 min((startX+x),(2*m-startX-x)) 수식을 사용했습니다. 가로 변, y=0 또는 y=n에 대해 대칭이동 할 때도 같은 방식으로 구해 두 거리 중 최소값을 return하도록 했습니다.
하지만 이 코드는 문제의 두 번째 제약조건을 반영하지 않은 코드입니다. 당구공의 시작 위치와 목표 위치가 x축 또는 y축과 평행한 경우, 가장 가까운 변에 대해 원 쿠션을 했을 때 당구공이 목표 위치를 두 번 지나는 경우가 발생합니다.
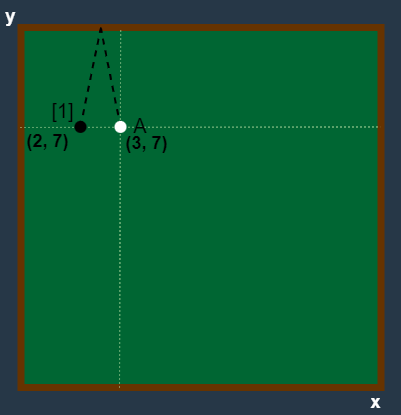
이는 문제의 두 번째 테스트 케이스에서 알 수 있습니다. 가장 가까운 왼쪽 벽에다 쿠션을 치면 (2,7)에서 출발한 당구공이 (3,7) 지점에 도착하기까지 (2,7) 지점을 두 번 지나게 됩니다.
따라서 이를 반영한 두 번째 코드입니다. 위와 같이 시작 위치와 목표 위치의 y좌표가 같을 때, 시작 지점의 x좌표가 목표 지점의 x좌표보다 크다면 왼쪽 변을 이용한 쿠션이 불가능합니다. 따라서 위쪽 변을 통한 대칭이동과 오른쪽 변을 이용한 대칭이동의 거리를 비교하는 방식을 사용했습니다. 좀 무식한 방식이지만 통과했습니다!
def solution(m, n, startX, startY, balls):
answer=[]
for ball in balls:
x, y = ball[0], ball[1]
if x == startX:
if y > startY :
answer.append(min((startY+y)**2,(y-startY)**2+4*min(x,m-x)**2))
else:
answer.append(min((2*n-startY-y)**2,(y-startY)**2+4*min(x,m-x)**2))
elif y == startY:
if x > startX:
answer.append(min((startX+x)**2,(x-startX)**2+4*min(y,n-y)**2))
else:
answer.append(min((2*m-startX-x)**2,(x-startX)**2+4*min(y,n-y)**2))
else:
answer.append(min((x-startX)**2+min(startY+y,2*n-startY-y)**2,(y-startY)**2+min(startX+x,2*m-startX-x)**2))
return answer