[프로그래머스] 두 원 사이 정수의 쌍 Lv.2 Python

문제 링크

1. 문제 설명

x축과 y축으로 이루어진 2차원 직교 좌표계에 중심이 원점인 서로 다른 크기의 원이 두 개 주어집니다. 반지름을 나타내는 두 정수 r1, r2가 매개변수로 주어질 때, 두 원 사이의 공간에 x좌표와 y좌표가 모두 정수인 점의 개수를 return하도록 solution 함수를 완성해주세요.
※ 각 원 위의 점도 포함하여 셉니다.

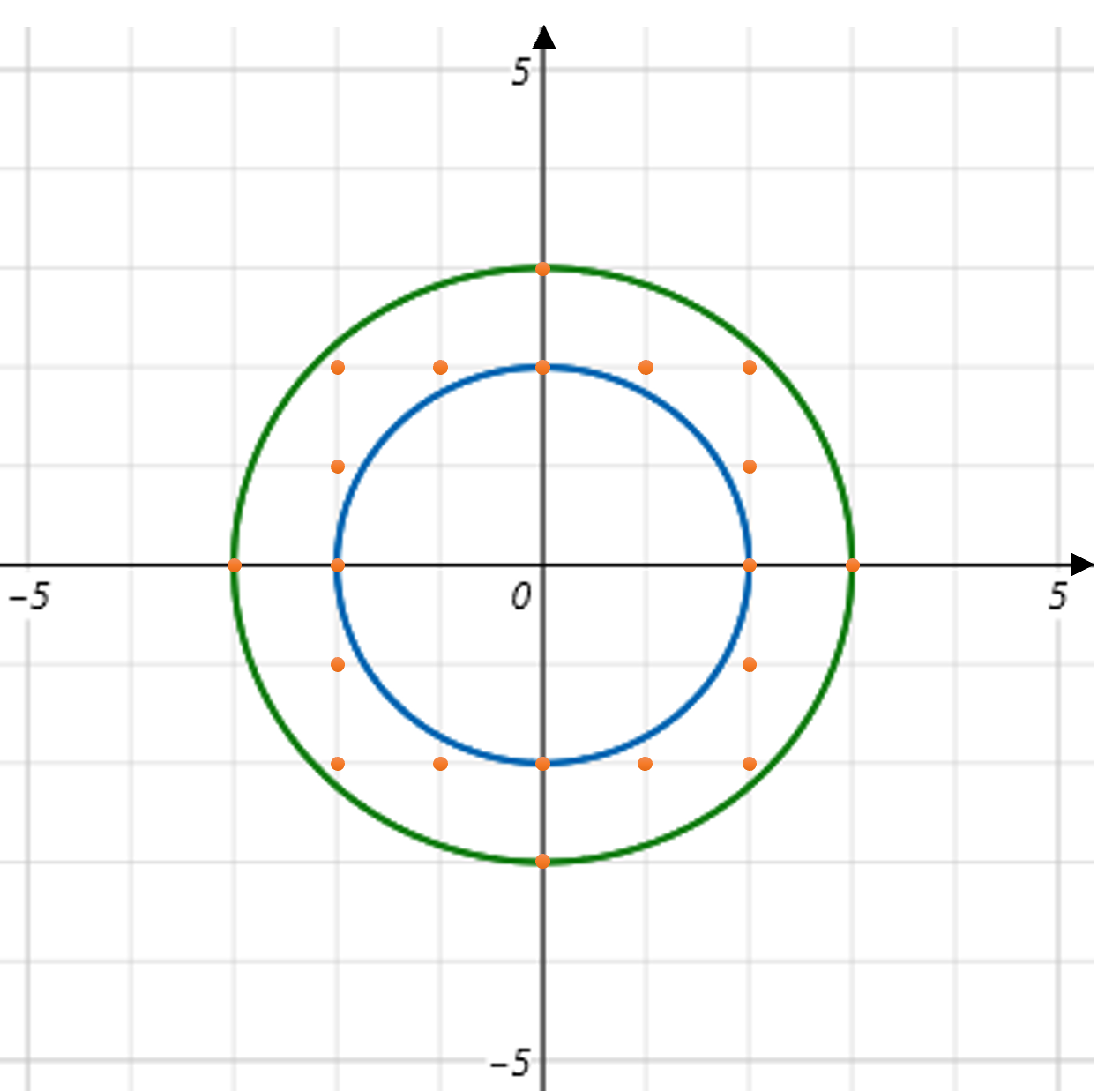
2. 문제 접근

저도 그렇고 대부분의 풀이는 1사분면만의 정수점 개수를 구해서 네 배를 곱하는 것입니다. 아이디어도 간단하고 설정할 범위도 명백합니다. 유의할 점은 1사분면 위의 점과 양의 x축, 양의 y축 위의 점들 중 한쪽만 포함시켜야 합니다.

범위를 설정하고 x축을 기준으로 점의 개수를 구할 때 int를 써서 소수점 아래를 버렸습니다. 위의 예제에서 x=1과 r2의 교점은 (1, 2.8..), r1의 교점은 (1,1.7..)이 됩니다. 그래서 int값은 2,1이 되므로 둘을 빼면 원하는 값인 1이 나옵니다.

다만 두 교점이 둘 다 정수인 경우 예외 처리가 필요합니다. 대표적으로 y축 위 교점은 (0,3), (0,2)이므로 뺄셈을 하면 1이 나오지만 필요한 값은 2입니다.

3 .문제 풀이

from math import sqrt

def solution(r1, r2):
    quar = 0
    for i in range(0, r1):
        quar += int(sqrt(r2**2 - i**2)) - int(sqrt(r1**2 - i**2 - 1))
    for i in range(r1, r2):
        quar += int(sqrt(r2**2 - i**2))
    return quar * 4

다양한 방법이 있겠지만 제가 생각한 가장 단순한 방법은 1을 빼서 자체적으로 내림 처리를 하는 겁니다. 이러면 r1 또는 r2의 교점이 정수일 때를 각각 고려할 필요도 없고 r1이 자연수이므로 자연수 i에 대해 $\sqrt{{r_1}^2 - {i^2} - 1}$의 값이 정수가 되거나 하는 걱정을 할 필요가 없습니다.