[프로그래머스] 표현 가능한 이진트리 Lv. 3 Python

문제 링크

1. 문제 설명

당신은 이진트리를 수로 표현하는 것을 좋아합니다.

이진트리를 수로 표현하는 방법은 다음과 같습니다.

이진수를 저장할 빈 문자열을 생성합니다.
주어진 이진트리에 더미 노드를 추가하여 포화 이진트리로 만듭니다. 루트 노드는 그대로 유지합니다.
만들어진 포화 이진트리의 노드들을 가장 왼쪽 노드부터 가장 오른쪽 노드까지, 왼쪽에 있는 순서대로 살펴봅니다. 노드의 높이는 살펴보는 순서에 영향을 끼치지 않습니다.
살펴본 노드가 더미 노드라면, 문자열 뒤에 0을 추가합니다. 살펴본 노드가 더미 노드가 아니라면, 문자열 뒤에 1을 추가합니다.
문자열에 저장된 이진수를 십진수로 변환합니다.
이진트리에서 리프 노드가 아닌 노드는 자신의 왼쪽 자식이 루트인 서브트리의 노드들보다 오른쪽에 있으며, 자신의 오른쪽 자식이 루트인 서브트리의 노드들보다 왼쪽에 있다고 가정합니다.

다음은 이진트리를 수로 표현하는 예시입니다.

주어진 이진트리는 다음과 같습니다.

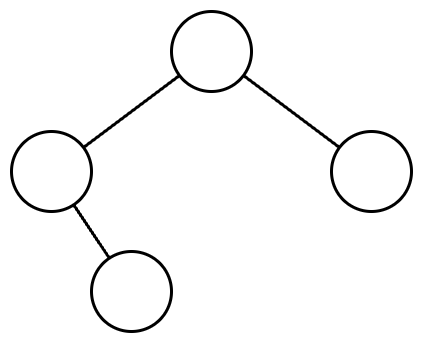
주어진 이진트리에 더미노드를 추가하여 포화 이진트리로 만들면 다음과 같습니다. 더미 노드는 점선으로 표시하였고, 노드 안의 수는 살펴보는 순서를 의미합니다.

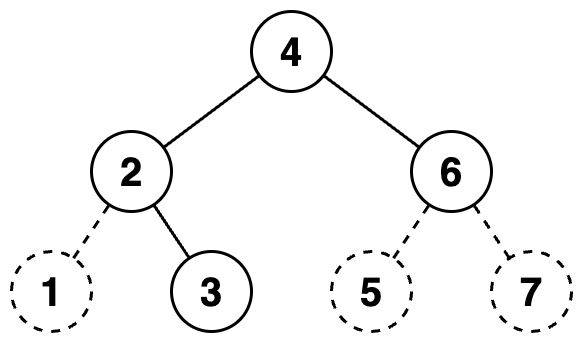
노드들을 왼쪽에 있는 순서대로 살펴보며 0과 1을 생성한 문자열에 추가하면 "0111010"이 됩니다. 이 이진수를 십진수로 변환하면 58입니다.

당신은 수가 주어졌을때, 하나의 이진트리로 해당 수를 표현할 수 있는지 알고 싶습니다.

이진트리로 만들고 싶은 수를 담은 1차원 정수 배열 numbers가 주어집니다. numbers에 주어진 순서대로 하나의 이진트리로 해당 수를 표현할 수 있다면 1을, 표현할 수 없다면 0을 1차원 정수 배열에 담아 return 하도록 solution 함수를 완성해주세요.

2. 문제 접근

문제에서 준 깊이 3의 포화 이진트리 예제를 살펴봅시다. 깊이가 3이고 더미 노드를 추가해 모든 자식 노드가 존재하므로 전체 노드의 수는 $2^3 -1 = 7$개입니다. 부모 노드는 가운데 4번 노드이고 4를 기준으로 하위 트리 1-2-3, 4-5-6 으로 나눠집니다.

하위 트리가 유효한 포화 이진트리가 되는지 확인하려면, 자식 노드에 부모 노드가 존재하는지만 확인하면 됩니다. 1-2-3 하위 트리에서, 부모 노드인 2번이 존재하지 않는데 1 또는 3번 노드가 존재할 수 없습니다. 하위 트리에서 부모 노드에 해당하는 2번 노드의 비트값이 0인데 1번, 3번 자식노드에 1인 비트값이 존재한다면 포화이진트리로 표현할 수 없는 수열이라 판단할 수 있습니다.

따라서 주어진 비트 수열이 포화이진트리로 표현할 수 있는지 판단하려면, 주어진 비트 수열을 부모 노드(가운데 숫자)를 중심으로 하위 노드로 나누기를 반복하면서, 만약에 부모 노드가 0인데 자식 노드가 1인 상황이 발생하는지만 확인하면 됩니다. 슬라이싱이 모두 끝나기 전에 이러한 경우가 발생하면 이 수열은 유효하지 않은 수열로 판단하고 검증을 종료합니다.

깊이가 n인 포화 이진트리의 노드 수는 $2^n -1$입니다. 그런데 당연히 임의의 수를 이진수로 변환했을 때 이진수의 길이가 $2^n -1$꼴이 될 것이라 보장할 수 없습니다. 예제의 58을 이진수로 변환하면 111010입니다. 길이가 6인 비트수열이므로 문제에서는 왼쪽에 빈 더미 노드(0)가 하나 있다고 가정합니다. 그래서 '111010'을 '0'*1 + '111010'으로 변환하는 과정이 필요합니다.

그렇다면 몇 개의 0을 더해야 할까요? 수열의 길이가 $p$이고, $2^n -1<p<2^{n+1} -1$이라면 수열의 길이가 $2^{n+1} -1$이 될 때까지 0을 더해야 합니다.
또한 $2^n<p + 1<2^{n+1}$ 이므로 $n=int(log_2{(p+1)})$ 을 통해 n의 값을 구할 수 있습니다.

따라서 문제는 크게 세 단계로 해결할 수 있습니다.

• 1. 주어진 수를 이진수 비트 수열로 변환하고 왼쪽에 임의의 개수만큼 0을 추가
• 2. 변환한 비트 수열에서 부모 노드(가장 가운데 비트)를 찾고 유효한 수열인지 확인
     (부모 노드가 0이라면 모든 자식 노드의 값이 0이여야 함)
• 3. 중심 노드를 기준으로 나누어 유효성 검증을 재귀적으로 반복

3 문제 풀이

import math

#부분 수열의 유효성 확인
def is_valid_sequence(sequence):
    length = len(sequence)
    middle_index = length // 2
    return not (length > 1 and sequence[middle_index] == '0' and '1' in sequence[:middle_index] + sequence[middle_index+1:])

# 재귀적 검증
def validate_sequence(sequence):
    if len(sequence) == 1:
        return is_valid_sequence(sequence)
    middle_index = len(sequence) // 2
    return is_valid_sequence(sequence) and validate_sequence(sequence[:middle_index]) and validate_sequence(sequence[middle_index+1:])

# 주어진 숫자 리스트를 포화 이진트리 비트수열로 변환, 검증
def solution(numbers):
    binary_seq = []
    for num in numbers:
        binary = bin(num)[2:]
        n = int(math.ceil(math.log2(len(binary) + 1)))
        binary = '0' * (2 ** n - 1 - len(binary)) + binary
        binary_seq.append(list(binary))
    return [1 if validate_sequence(seq) else 0 for seq in binary_seq]

bin 함수를 사용해 이진수로 변환하면 앞에 0b 접두사가 붙기 때문에 원하는 비트수열을 얻으려면 슬라이싱을 해줘야 합니다.