회귀분석 1. Intro

회귀분석(Regression Analysis)이란

넓은 의미의 회귀분석은 독립변수 x로 종속변수 y를 예측하는 것을 말합니다.
좀 더 구체적으로 말하자면, 관측된 연속형 변수들에 대해 두 변수 사이의 모형을 구한 뒤 적합도를 측정해 내는 분석 방법입니다.

회귀분석의 유래

Regression, 회귀라는 단어 자체의 뜻은 원래의 상태로 돌아가는 것을 의미합니다.
회귀분석은 영국의 유전학자 Francis Galton에 의해 처음 발전되었습니다. 그는 부모의 키와 아이들의 키 사이의 관계를 연구하였고 키가 작은 부모에서의 자녀의 키와 키가 큰 부모에서의 자녀의 키 둘 다 그룹의 평균에 되돌아가거나 회귀한다는 경향을 밝혀냈습니다.

현대에서 '회귀'는 변수들 사이의 통계적 관계를 설명하는 용어로 굳어져 사용되고 있습니다.

회귀분석을 통해 얻을 수 있는 정보

1. 회귀계수
   독립변수의 변화가 종속변수를 얼마나 변화시키는가?
2. 모형적합도
   모형이 데이터에 얼마나 적합한가?

기본 개념

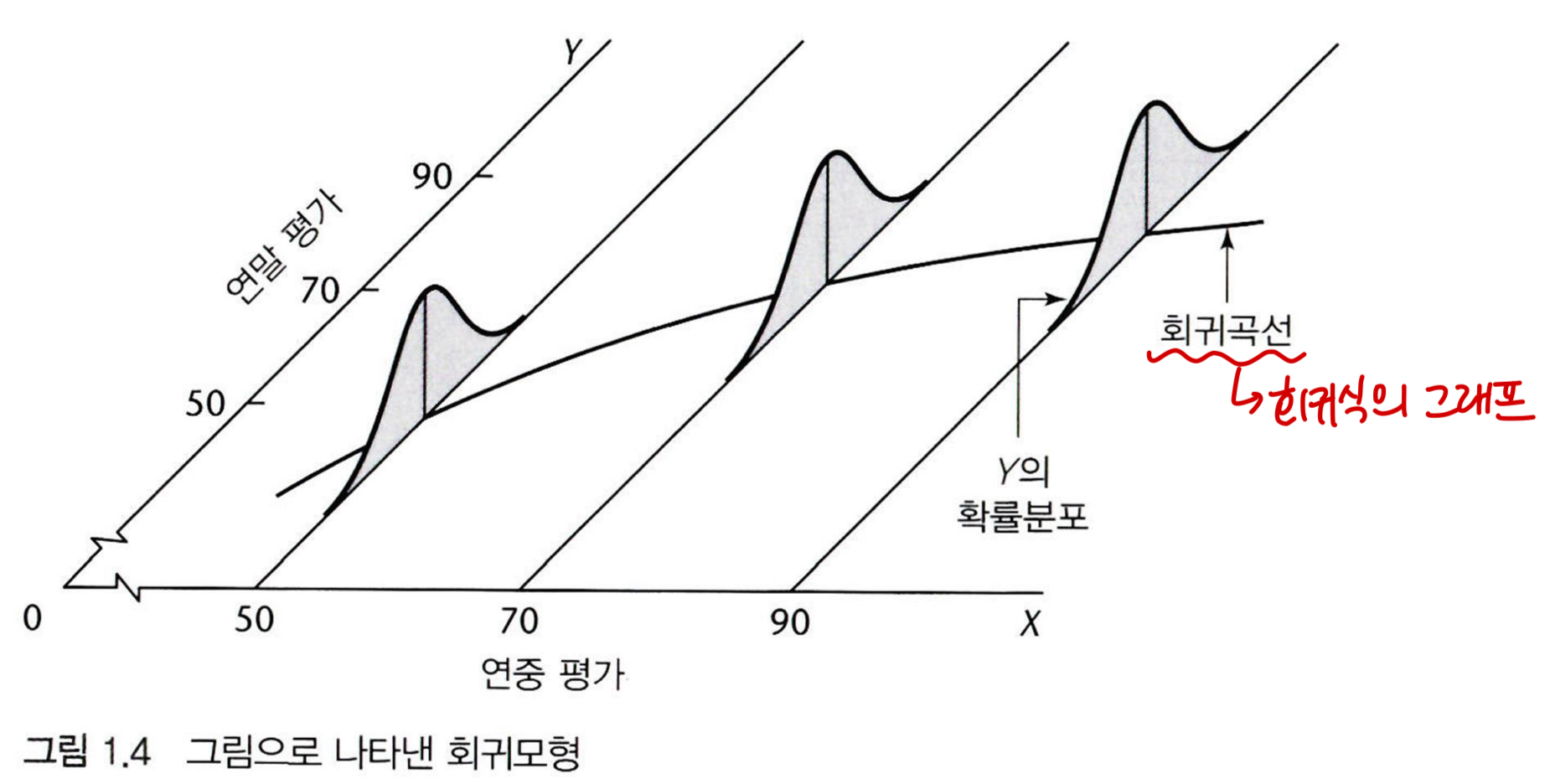
회귀모형은 통계적 관계의 두 필수적인 요소를 표현하는 형식 수단입니다.

1. 반응변수 Y가 예측변수 X에 의하여 체계적으로 변하는 경향
2. 통계적 관계의 선 근방에 흩어진 점

이 두 특성은 다음을 가정함으로써 회귀모형에서 구현됩니다.

1. X의 각 수준에 따라 Y의 확률분포가 존재한다.
2. 확률분포의 평균은 X에 의해 체계적으로 변한다.
   이 체계적 관계를 X에 대한 Y의 회귀식으로 나타냅니다. 회귀식은 회귀모형에 포함되는 개념이라고 볼 수 있습니다.

저는 개인적으로 회귀모형과 회귀식의 차이가 헷갈렸는데, 회귀식은 "확률분포의 평균"에 대한 식이라는 점을 기억해두시면 좋을 것 같습니다.

회귀분석의 기본 모형

하나의 종속변수와 하나의 독립변수 간의 관계를 분석하는 것을 단순회귀분석(simple regression analysis), 하나의 종속변수와 여러 독립변수 사이의 관계를 분석하는 것을 다중회귀분석(multiple regression analysis)라고 합니다.

먼저 가장 기본적인 회귀 모형을 보겠습니다.

• $Y_i$: i번째 시행의 반응변수 관측값입니다. Y는 Response variable이라고 부릅니다.
• $X_i$: 우리에게 주어진 데이터로, i번째 시행의 예측변수 관측값입니다. X는 Predictor variable이라고 부릅니다.
• $\beta_0, \beta_1$: 회귀모형의 모수입니다. 회귀계수(regression coefficients)라고 합니다.
• $\epsilon_i$: 평균이 0이고 분산이 $\sigma^2$인 오차항입니다.
• $i$: 1, ..., n

이 모형은 직선의 방정식으로 표현되고 있는 일차모형입니다. 이 모형에서 중요하게 기억해야 할 특징들을 살펴보겠습니다.

1. 확률변수 $Y_i$

$Y_i$는 상수값 $\beta_0 + \beta_1 X_i$과 확률적 오차항 $\epsilon_i$로 구성됩니다. 따라서 $Y_i$는 확률변수입니다.

2. $E(Y_i)=\beta_0+\beta_1X_i$

$E(\epsilon_i)=0$이므로,

확률분포의 평균인 회귀식을 유도해본 결과 회귀모형과 상당히 비슷하게 생긴 걸 알 수 있습니다.

3. $\epsilon_i = Y_i-\hat Y_i$

반응변수 $Y_i$는 $\epsilon_i$만큼 회귀식의 값을 초과하거나 미달합니다.

4. 모든 오차항 $\epsilon_i$는 등분산성을 가정합니다.

따라서 모든 $Y_i$도 분산이 같습니다.

따라서 위의 회귀모형은 예측변수 X의 수준($X_i$)과 관계없이 Y들의 확률분포의 모든 분산 $\sigma^2$은 같다고 가정합니다.

5. $\epsilon_i$와 $\epsilon_j$는 상관관계가 없으며 두 값의 공분산은 0으로 가정합니다.

$\epsilon_i$와 $\epsilon_j$가 서로 독립이므로 반응변수 $Y_i$와 $Y_j$도 서로 독립입니다.

정리하자면, 위의 회귀모형은 반응변수 $Y_i$는 평균이 $E(Y_i)=\beta_0+\beta_1X_i$이고 X의 모든 수준에 대해 동일한 분산 $\sigma^2$인 확률분포에서 나옵니다. 또한 $Y_i$와 $Y_j$는 서로 독립입니다.

예시

회귀모형이 다음과 같을 때,

회귀식은 다음과 같을 것입니다.

$X_i=45$이고 $Y_i=108$ 일 때

따라서 $\epsilon_i=4$ 가 나옵니다. 이는 평균값 $E(Y_i)$로부터의 $Y_i$의 편차를 의미합니다.

회귀모형의 대안 형태

회귀모형의 대안으로 쓰이는 두 가지 형태가 있습니다.

1. $X_0$을 1인 상수값이라고 가정하면, 회귀모형을 다음과 같이 표현할 수 있습니다.
   $Y_i=\beta_0X_0+\beta_1X_i+\epsilon_i$
2. $X_i$ 대신 편차 $X_i-\bar X$ 를 예측변수로 사용할 수 있습니다.
   $\begin{gathered} Y_i=\beta_0+\beta_1\left(X_i-\bar{X}\right)+\beta_1 \bar{X}+\varepsilon_i \\ =\left(\beta_0+\beta_1 \bar{X}\right)+\beta_1\left(X_i-\bar{X}\right)+\varepsilon_i \\ =\beta_0^*+\beta_1\left(X_i-\bar{X}\right)+\varepsilon_i \\ \\ Y_i=\beta_0^*+\beta_1\left(X_i-\bar{X}\right)+\varepsilon_i \\ \beta_0^*=\beta_0+\beta_1 \bar{X} \end{gathered}$