알고리즘 전략 - Decrease-and-Conquer

1. Decrease-and-Conquer란?

• Decrease-and-Conquer란 문제를 더 작은 instance로 쪼개나가며 축소시킨 문제를 해결하는 방식이다.

• 크게 Top down 방식과 Bottom up 방식이 있다.
  • Top down : 맨 위에서부터 축소시킨 문제를 재귀적으로 해결하는 방식
    (Ex. reculsive for Fibonacci)
  • Bottom up : 가장 작은 instance(맨 아래)부터 반복적으로 쌓아올려 해결하는 방식
    (Ex. loop for Fibonacci, 때로는 이 방식은 brute force한 방식과 동일하기도 함.)

• Decrease by a constant (usually by 1)
  • 상수만큼 빼면서 문제를 축소시키는 방식
    (ex. $n$ -> $n-1$ -> $n-2$ -> ...)
• Decrease by a constant factor (usually by half)
  • 상수만큼 나누면서 문제를 축소시키는 방식
    (ex. $n$ -> $n/2$ -> $n/2^2$ -> ...)
• Variable-size Decrease
  • 문제를 축소시킬 때의 크기가 정해져있지 않은 방식
    (ex. 유클리드 알고리즘 - 최대공약수 구하기)
    
    

2. Decrease by a constant - Insertion Sort

• Insertion Sort (삽입 정렬) 은 $n$개의 원소가 있을 때, $n$번째 원소를 나머지 $n-1$개의 원소로 이루어진 '이미 정렬된' 배열에 삽입하는 방식이다.

• 이 때, '이미 정렬된' 이란 재귀적으로 함수를 호출한다는 의미이고, 결국 1, 2번째 원소를 정렬한 뒤 3번째 원소를 그 사이에 알맞게 삽입하고 그 다음 4번째 원소를 그 사이에 삽입하고...를 반복하게 된다.

• 아이디어는 재귀적이지만, 결국 맨 아래부터 정렬한 뒤 그 다음 원소를 삽입하는 방식이기 때문에 알고리즘 설계시에는 bottom 방식으로 loop문을 사용한다.

• 알고리즘 과정
  1) 일단, 1, 2번째 원소를 비교하여 정렬한다.
  2) 3번째 원소를 이미 정렬된 배열의 맨 오른쪽 원소와 크기를 비교하여 한칸씩 왼쪽으로 움직이는 방식으로 삽입한다.
  3) 쭉 반복하여 마지막 n번째 원소를 이미 정렬된 배열에 삽입하면 끝난다.

• 알고리즘 의사 코드
  

• 알고리즘 예시
  

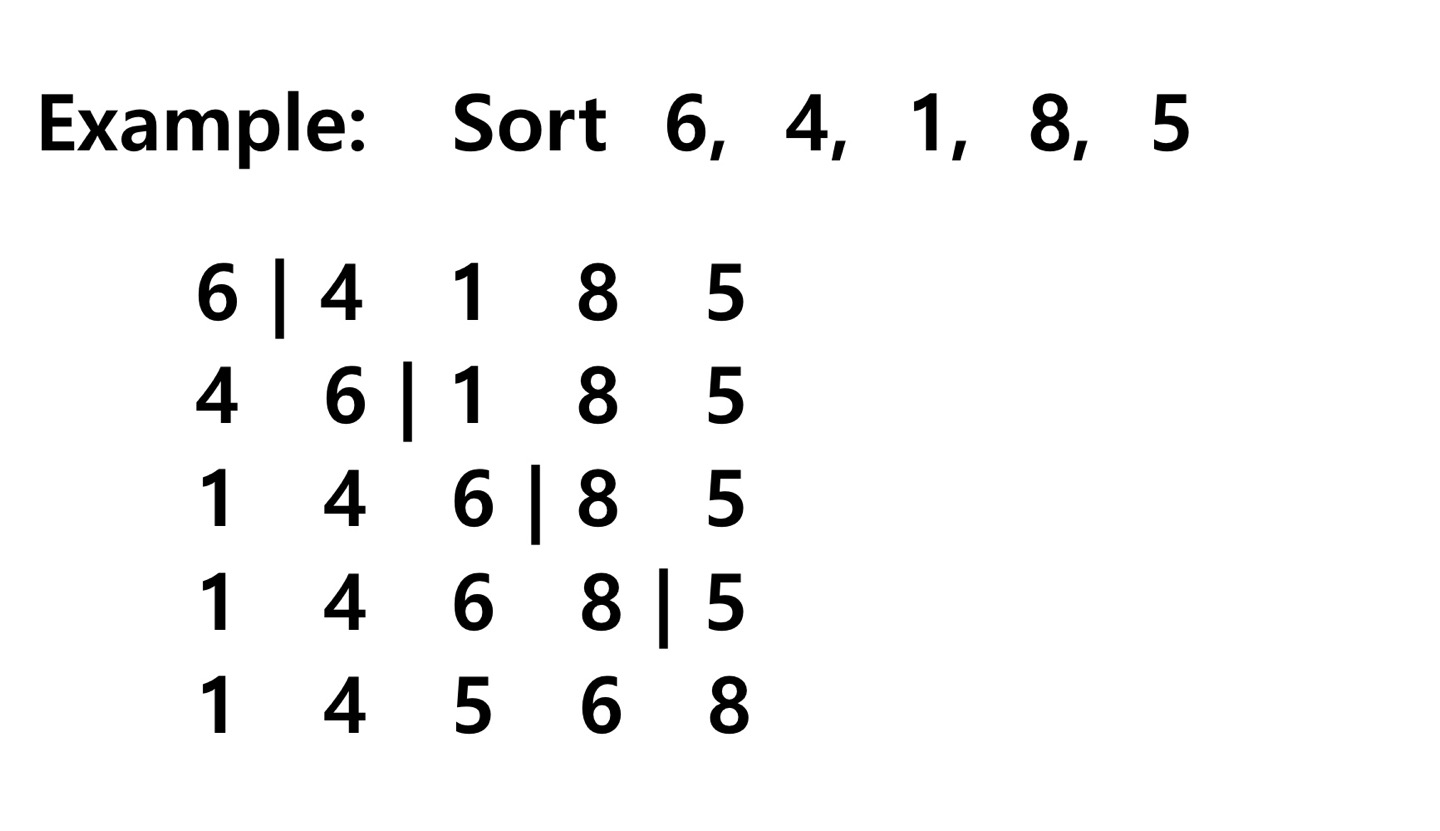
• 알고리즘 특징
  • basic operation = key comparison $A[j] > v$
  • 시간복잡도
    • worst case = $\Theta(n^2)$
    • best case = $\Theta(n)$
    • avg case = $\Theta(n^2)$

3. Decrease by a constant - Topological Sort

• Topological Sort (위상정렬) 은 방향을 가지는 graph(no cycle)에서 방향 순서에 맞게 모든 노드들을 나열하는 문제이다.
  (ex. 작업 순서 정렬)
• Directed acyclic graph (dag)란, 위에서 말한 방향성을 가지되 순환구조는 없는 그래프를 의미한다. 이 때, 어떤 노드로 들어오는 간선의 수를 진입 차수, 그 노드에서 나가는 간선의 수를 진출 차수라고 한다.
• 그래프에는 반드시 진입차수가 0인 노드가 있어야하고, 정렬은 이 노드들부터 시작한다.

• Depth-First Search를 이용한 Topological Sort
  1) 일단, 진입차수가 모든 0인 노드들부터 dfs를 실시하고 dfs를 한번이라도 호출한 노드는 '이미 호출된 노드' 배열에 추가한다.
  2) dfs를 호출하게 되면 해당 노드에서 진출하는 간선을 통해 연결되는 노드들에 대해 다시 dfs를 호출한다. (재귀적으로)
  3) 만약, dfs를 호출한 노드가 더 이상 진출 간선이 없다면 해당 노드를 STACK에 저장한다. 모든 노드들에 대해서 dfs 호출이 끝나게 되면 STACK에 있는 노드들을 하나씩 pop하여 배열을 만들어 출력한다.
  4) DFS의 의사 코드
  

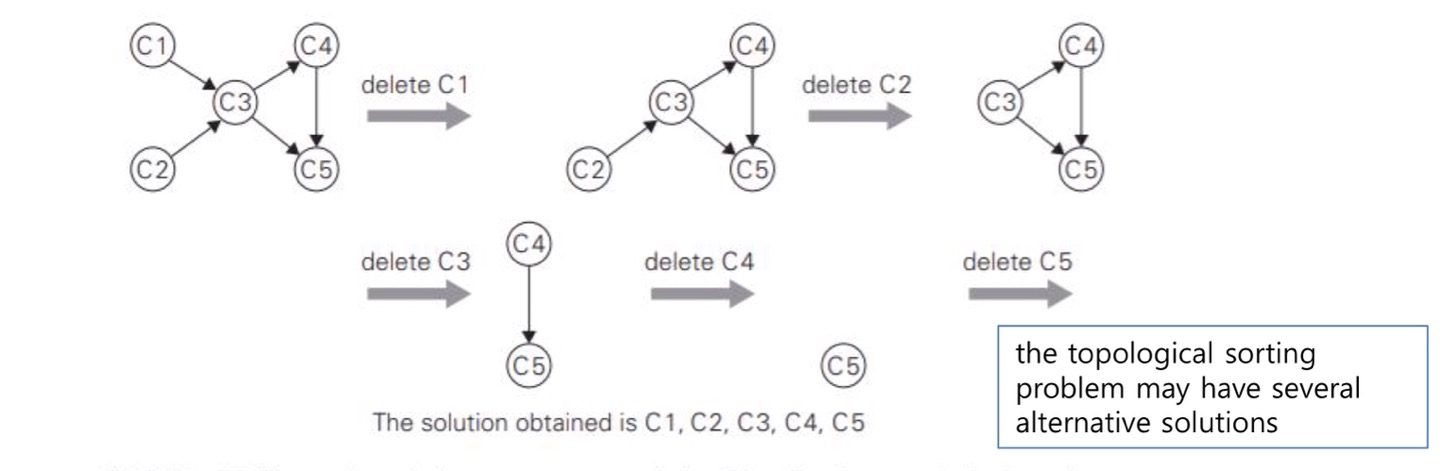
• Source-removal algorithm을 이용한 Topological Sort
  • 이 방식은 단순히 호출된 노드를 지운 그래프에 대해서 다시 문제를 푸는 방식이다.
  • 1개의 노드씩 줄여나가며 문제를 축소시키면서 지운 노드는 차례로 solution 배열에 나열된다.
  • 그래프의 모든 노드가 지워졌을 때 solution 배열에 있는 노드들을 그 순서 그대로 출력한다.
  • 알고리즘 예시
    

4. Decrease by a constant factor - Binary Search

• Binary Search (이진 탐색)은 이미 정렬된 배열에서 매우 높은 효율성을 보이는 알고리즘이다.
• 배열의 위치한 원소를 확인한 후, 원하는 값보다 크면 왼쪽 set으로 작으면 오른쪽 set으로 이동하여 탐색하는 배열의 크기를 계속해서 $1/2$로 쪼개어 나가는 방식이다.

• 알고리즘 예시 및 의사 코드
  

5. Decrease by a constant factor - Fake-Coin Problem

• $n$개의 코인이 있을 때, 단 한개의 코인이 가짜로 무게가 더 가볍다고 했을 때, 이 코인을 찾는 문제이다.
• 2개의 set으로 나누어 저울질하여 가벼운 쪽의 set으로 문제를 축소시켜 반복하는 알고리즘이다.
  • 만약에 set 안에 코인이 홀수개라면, 한개를 제외하고 저울질하면 된다.
    
    

6. Decrease by a constant factor - Russian Peasant Multiplication

• 이 문제는 모든 곱셈을 $\times 2$와 $\div2$와 덧셈만으로 표한하는 알고리즘이다.
• 어떤 두 수 $n, m$을 곱할 때, 작은 수를 왼쪽에 두고 왼쪽은 2로 나누며 아래로 쭉 써주고, 오른쪽은 2를 곱하며 아래로 쭉 써준다.
• 이 때, 왼쪽 수를 나눌 때에는 나머지는 항상 버리는 방향으로 나눈다.
• 이제, 왼쪽 수가 짝수인 행은 없애고, 남은 행에서 오른쪽 수들을 모두 더하면 답이 나온다.
  
  

7. Decrease by a constant factor - Josephus Problem

• 이 문제는 $(n, k)$ 요세푸스 순열에서 가장 오른쪽의 원소를 구하는 알고리즘이다.
• $(n, k)$ 요세푸스 순열이란, $n$명의 사람이 원을 그리고 앉았을 때, 첫번째 사람부터 순서를 세어 $k$번째 사람을 제외하고 그 다음 사람부터 다시 또 $k$번째 사람을 제외하는 과정을 반복하였을 때, 제외되는 사람의 번호를 나열한 것이다.
• 이 때, 이 순열의 가장 마지막 사람의 번호를 알아내는 것이 이 알고리즘의 목적이다.

8. Variable-size Decrease - The Selection Problem

9. Variable-size Decrease - Interpolation Search

10. Variable-size Decrease - Binary Search Tree