최소 신장 트리(MST), 크루스칼, 프림 알고리즘

🖥️최소 신장 트리의 정의

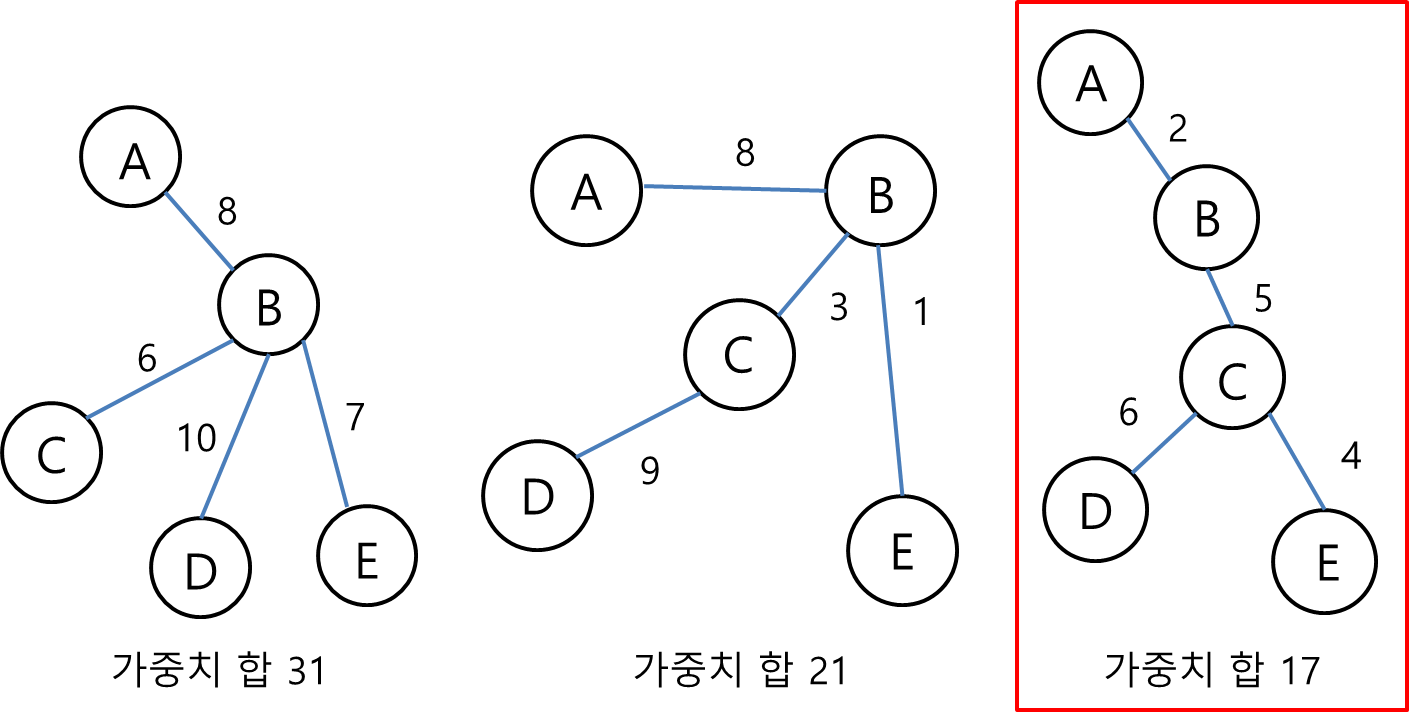
1. 모든 노드를 연결 할 것
2. 노드 전체를 한바퀴 도는 사이클이 없을 것
3. 간선의 개수가 전체 노드의 개수보다 하나 적을 것
4. 간선을 이동하는 거리를 합쳤을 때 가장 낮은 가중치를 가지는 것이 최소 신장 트리

최소 신장 트리 알고리즘

1. 크루스칼 알고리즘
2. 프림 알고리즘

크루스칼(Kruskal) 알고리즘

그래프의 간선을 하나씩 늘리며 MST를 만든다.
전체 그래프의 간선을 가중치에 따라 정렬한 후 사이클을 형성하지 않는 간선을 하나씩 추가하면서 MST를 만든다.
유니온 파인드 자료구조를 사용한다.
O(ElogV)의 시간복잡도를 가진다.
간선이 적은 그래프에서 효율적이다.

import java.util.*;

class Edge implements Comparable<Edge> {
    int src, dest, weight;

    public Edge(int src, int dest, int weight) {
        this.src = src;
        this.dest = dest;
        this.weight = weight;
    }

    @Override
    public int compareTo(Edge other) {
        return this.weight - other.weight;
    }
}

class Subset {
    int parent, rank;
}

public class KruskalAlgorithm {
    int vertices, edges;
    Edge[] edge;

    KruskalAlgorithm(int vertices, int edges) {
        this.vertices = vertices;
        this.edges = edges;
        edge = new Edge[edges];
        for (int i = 0; i < edges; ++i)
            edge[i] = new Edge(0, 0, 0);
    }

    int find(Subset[] subsets, int i) {
        if (subsets[i].parent != i)
            subsets[i].parent = find(subsets, subsets[i].parent);
        return subsets[i].parent;
    }

    void union(Subset[] subsets, int x, int y) {
        int rootX = find(subsets, x);
        int rootY = find(subsets, y);

        if (subsets[rootX].rank < subsets[rootY].rank) {
            subsets[rootX].parent = rootY;
        } else if (subsets[rootX].rank > subsets[rootY].rank) {
            subsets[rootY].parent = rootX;
        } else {
            subsets[rootY].parent = rootX;
            subsets[rootX].rank++;
        }
    }

    void kruskalMST() {
        Edge[] result = new Edge[vertices];
        int e = 0;  // Index used in result[]
        int i = 0;  // Index used to pick next edge

        for (i = 0; i < vertices; ++i)
            result[i] = new Edge(0, 0, 0);

        Arrays.sort(edge);

        Subset[] subsets = new Subset[vertices];
        for (i = 0; i < vertices; ++i)
            subsets[i] = new Subset();

        for (int v = 0; v < vertices; ++v) {
            subsets[v].parent = v;
            subsets[v].rank = 0;
        }

        i = 0;

        while (e < vertices - 1) {
            Edge nextEdge = edge[i++];

            int x = find(subsets, nextEdge.src);
            int y = find(subsets, nextEdge.dest);

            if (x != y) {
                result[e++] = nextEdge;
                union(subsets, x, y);
            }
        }

        System.out.println("Following are the edges in the constructed MST");
        for (i = 0; i < e; ++i)
            System.out.println(result[i].src + " -- " + result[i].dest + " == " + result[i].weight);
    }

    public static void main(String[] args) {
        int vertices = 5;  // Number of vertices in graph
        int edges = 7;  // Number of edges in graph
        KruskalAlgorithm graph = new KruskalAlgorithm(vertices, edges);

        // add edge 0-1
        graph.edge[0] = new Edge(0, 1, 10);
        // add edge 0-2
        graph.edge[1] = new Edge(0, 2, 6);
        // add edge 0-3
        graph.edge[2] = new Edge(0, 3, 5);
        // add edge 1-3
        graph.edge[3] = new Edge(1, 3, 15);
        // add edge 2-3
        graph.edge[4] = new Edge(2, 3, 4);
        // add edge 1-2
        graph.edge[5] = new Edge(1, 2, 7);
        // add edge 3-4
        graph.edge[6] = new Edge(3, 4, 9);

        graph.kruskalMST();
    }
}

프림(Prim) 알고리즘

시작 정점에서 점진적으로 MST를 확장한다.
MST에서 연결된 정점들 중에서 가장 가중치가 적은 간선을 선택하여 새로운 정점을 추가한다.
모든 그래프에서 정점이 연결된 상태에서 작동한다.
우선순위 큐 사용한다.
O(E log V)의 시간복잡도를 가진다.
간선이 많은 그래프에서 효율적이다.

import java.util.*;

class Graph {
    private int vertices;
    private LinkedList<Edge>[] adjacencyList;

    class Edge implements Comparable<Edge> {
        int dest, weight;

        Edge(int dest, int weight) {
            this.dest = dest;
            this.weight = weight;
        }

        @Override
        public int compareTo(Edge other) {
            return this.weight - other.weight;
        }
    }

    Graph(int vertices) {
        this.vertices = vertices;
        adjacencyList = new LinkedList[vertices];
        for (int i = 0; i < vertices; ++i)
            adjacencyList[i] = new LinkedList<>();
    }

    void addEdge(int src, int dest, int weight) {
        Edge edge1 = new Edge(dest, weight);
        Edge edge2 = new Edge(src, weight);
        adjacencyList[src].add(edge1);
        adjacencyList[dest].add(edge2);
    }

    void primMST() {
        boolean[] mstSet = new boolean[vertices];
        Edge[] edgeTo = new Edge[vertices];
        int[] key = new int[vertices];

        PriorityQueue<Edge> pq = new PriorityQueue<>(vertices, Comparator.comparingInt(o -> o.weight));

        for (int i = 0; i < vertices; ++i) {
            key[i] = Integer.MAX_VALUE;
            edgeTo[i] = new Edge(-1, Integer.MAX_VALUE);
        }

        key[0] = 0;
        pq.add(new Edge(0, key[0]));

        while (!pq.isEmpty()) {
            Edge edge = pq.poll();
            int u = edge.dest;

            mstSet[u] = true;

            for (Edge adj : adjacencyList[u]) {
                int v = adj.dest;
                int weight = adj.weight;

                if (!mstSet[v] && weight < key[v]) {
                    key[v] = weight;
                    pq.add(new Edge(v, key[v]));
                    edgeTo[v] = new Edge(u, weight);
                }
            }
        }

        System.out.println("Following are the edges in the constructed MST");
        for (int i = 1; i < vertices; ++i)
            System.out.println(edgeTo[i].dest + " -- " + i + " == " + edgeTo[i].weight);
    }

    public static void main(String[] args) {
        int vertices = 5;
        Graph graph = new Graph(vertices);

        graph.addEdge(0, 1, 2);
        graph.addEdge(0, 3, 6);
        graph.addEdge(1, 2, 3);
        graph.addEdge(1, 3, 8);
        graph.addEdge(1, 4, 5);
        graph.addEdge(2, 4, 7);
        graph.addEdge(3, 4, 9);

        graph.primMST();
    }
}