많은 트리의 모습 중, 가장 간단하고 많이 사용하는 이진 트리(binary tree)와 이진 탐색 트리(binary search tree)에 대해 알아본다.

이진 트리(binary tree)

이진 트리(Binary tree)는 자식 노드가 최대 두 개인 노드들로 구성된 트리입니다. 이 두 개의 자식 노드는 왼쪽 자식 노드와 오른쪽 자식 노드로 나눌 수 있습니다.

이진트리 종류

이진 트리는 자료의 삽입, 삭제 방법에 따라 정 이진 트리(Full binary tree), 완전 이진 트리(Complete binary tree), 포화 이진 트리(Perfect binary tree)로 나뉩니다

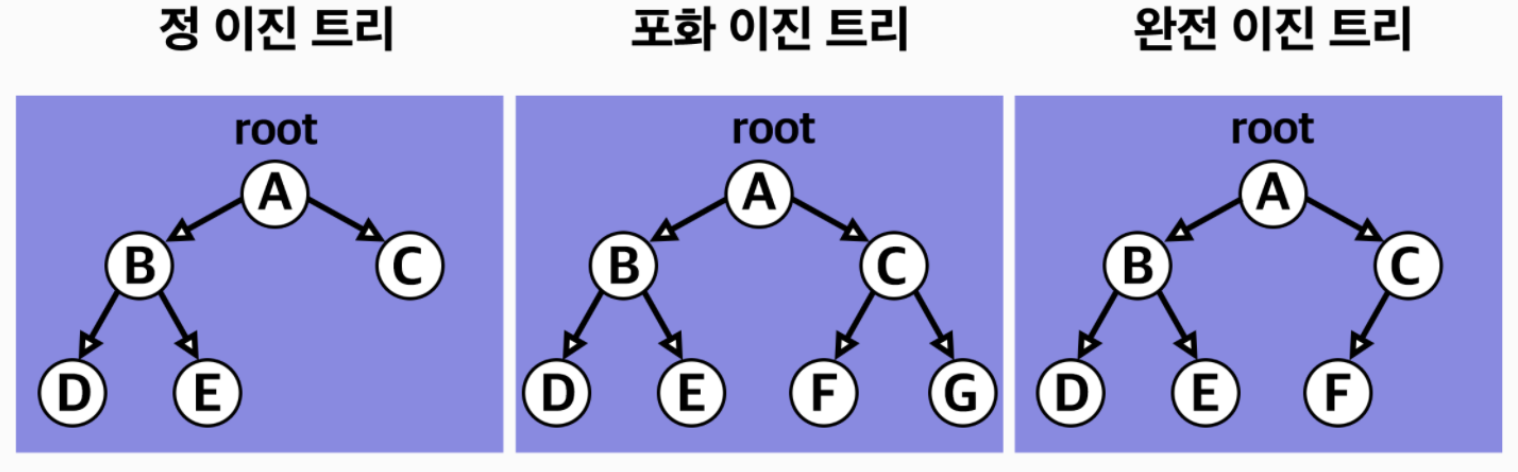
• 정 이진 트리(Full binary tree) : 각 노드가 0 개 혹은 2 개의 자식 노드를 갖습니다.
• 포화 이진 트리(Perfect binary tree) : 정 이진 트리이면서 완전 이진 트리인 경우입니다. 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리입니다.
• 완전 이진 트리 (Complete binary tree) : 마지막 레벨을 제외한 제외한 모든 노드가 가득 차 있어야 하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽이 채워져야 한다.

이진탐색트리(Binary Search Tree)

이진 탐색 트리는 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징이 있다.

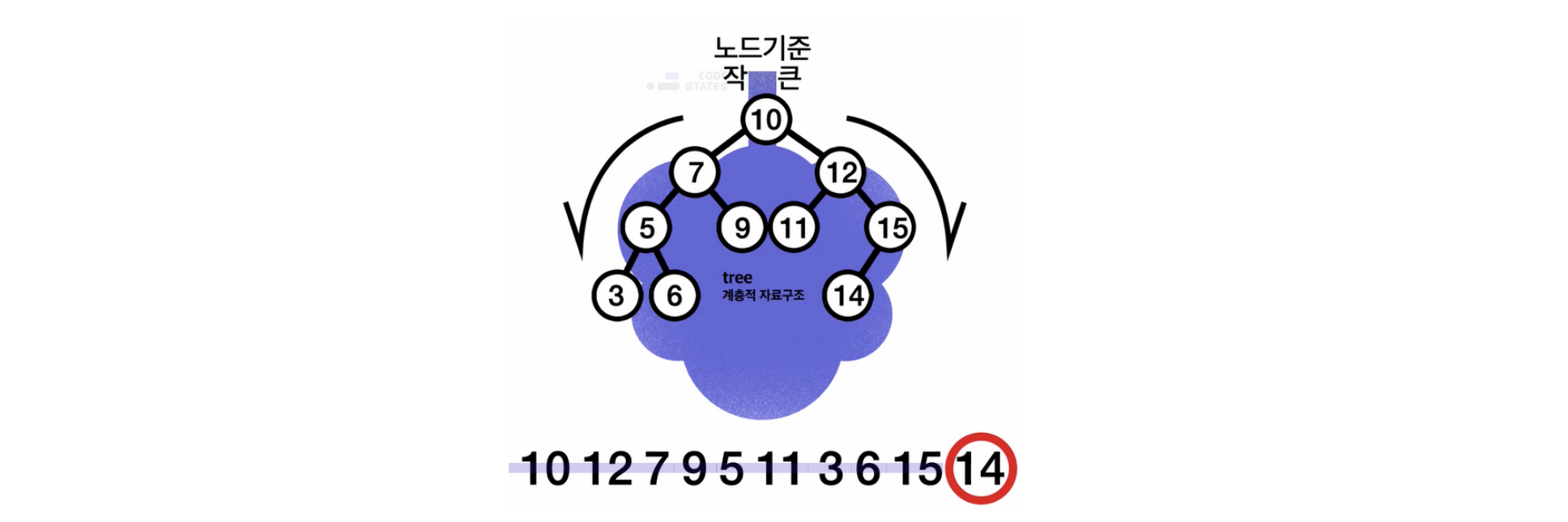
• 10부터 차례대로 넣어본다면? 이런방식이다.

예시) [10, 12, 7, 9, 5, 11, 3, 6, 15, 14]

1. 루트노드 : 10
2. 7은? 10보다 작아서 왼쪽노드로!
3. 12는? 10보다 크기때문에 오른쪽 노드로!
4. 9는? 루트노드 10보단 작아서 왼쪽 노드로 그러나 부모노드 7보단 커서 7의 오른쪽 노드에 넣는다.

이진탐색(Binary Serch)

• 분할정복 방법 : 반씩 범위를 나누어 가면서 분할정복하여 필요없는 부분은 버리고 찾는 값을 찾아가는 방법
• 장점 : 속도가 빠르다.
• 단점 : 자료구조안의 데이터가 정렬이 되어있어야한다.
  

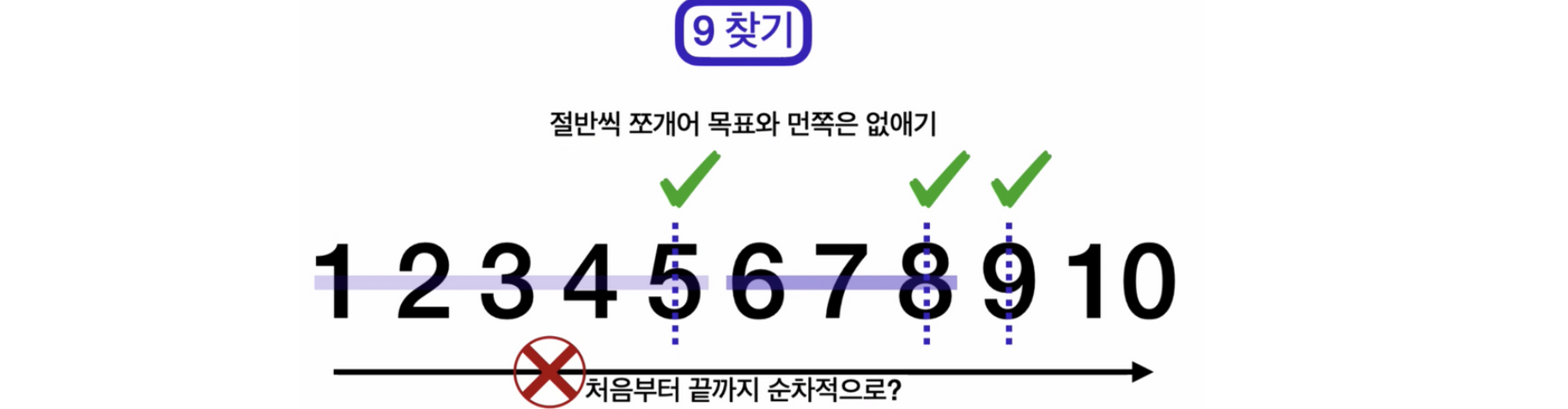
  예) 배열 = [ 1 ~10] → 만약 9를 찾는다면?
  → 이제 가운데 값은 6부터 10의 중간인 8이 된다.
  → 가운데 값인 8과 찾는 값 9를 비교하여 8이 작다면? 8까지의 배열요소를 버린다.

  • 짝수개의 요소일때는 보통 중간에서 앞에 값을 중간값이라 한다.
    → 9, 10 중 중간값은 9이고 9와 찾는 값 9가 같다! 찾음
  • 만약 10을 찾는 중이여서 갖지 않았다면 9을 버리고 유일한값 10만 남아서 찾게된다.

출처
코딩하는 거니 https://www.youtube.com/watch?v=Vfg6-AWGsCw&list=PLLcbGhhl4sQCiZxLuqDDDH6q-rc4wyaKe&index=7
코드스테이츠