프로그래머스 문제 - 산 모양 타일링

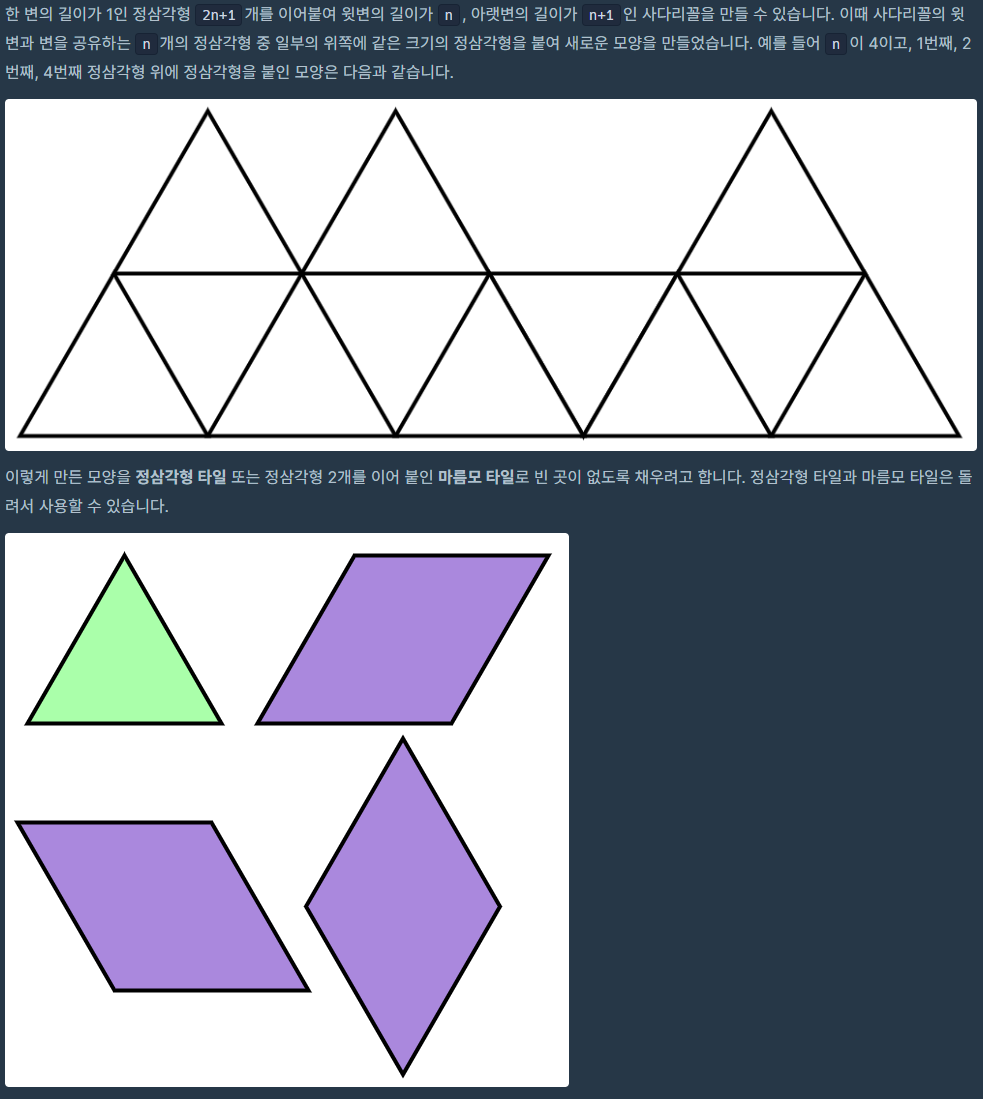
프로그래머스 산 모양 타일링 문제 풀이를 진행하였습니다.

문제 해석

문제를 읽으면 아래와 같은 해석이 가능합니다.

위의 삼각형들을 정삼각형 타일과 마름모 타일로 빈 곳 없이 채울 때 가능한 경우의 수를 구해야합니다.

문제 풀이

하나의 삼각형에는 위에 삼각형이 있을 경우 4가지, 없을 경우 3가지만큼 경우의 수를 가질 수 있습니다.
그리고 위쪽에 삼각형이 있든 없든 두 삼각형끼리는 한 개의 삼각형이 겹치게 됩니다.
겹쳤을 때의 경우의 수와 겹치지 않았을 때의 경우의 수를 각각 계산하며 순서대로 누적합을 구하면 답을 구할 수 있을 것입니다.

왼쪽에서 오른쪽으로 계산을 진행하기 때문에 왼쪽과 가운데만 사용하여 나오는 경우의 수와 오른쪽만을 사용하여 나오는 경우의 수를 따로 저장해줍니다.
n위치의 삼각형까지의 경우의 수를 구하기 위해서는
위에 삼각형이 있다면 3 * left[n-1] + 2 * right[n-1] 값이 왼쪽 값이 되며 left[n-1] + right[n-1]값이 오른쪽 값이 됩니다.
위에 삼각형이 없다면 갯수가 1가지 적어지게 되어 2 * left[n-1] + right[n-1] 값이 왼쪽 값이 되며 left[n-1] + right[n-1]값이 오른쪽 값이 됩니다.
그리고 n까지의 삼각형의 경우의 수는 left[n] + right[n]가 됩니다.

여기서 주의할 점은 모든 값에 10007의 나머지값으로 계산을 해주어야 정상적으로 정답이 나오게 됩니다.

전체 코드

#include <bits/stdc++.h>
#include <string>
#include <vector>

using namespace std;

int solution(int n, vector<int> tops) {
    int answer = 0;
    vector<int> leftValue(n+1, 0);
    vector<int> rightValue(n+1, 0);
    
    //처음 삼각형의 갯수
    rightValue[1] = 1;
    leftValue[1] = tops[0] == 1 ? 3 : 2;
    //다음 삼각형의 갯수
    for(int i = 2; i <= tops.size(); i++)
    {
        if(tops[i-1] == 1)
            leftValue[i] = ((3 * leftValue[i-1]) + (2 * rightValue[i-1])) % 10007;
        else
            leftValue[i] = ((2 * leftValue[i-1]) + rightValue[i-1]) % 10007;
        rightValue[i] = (leftValue[i-1] + rightValue[i-1]) % 10007;
    }
    answer = (leftValue[n] + rightValue[n]) % 10007;
    return answer;
}

출저

https://school.programmers.co.kr/learn/courses/30/lessons/258705