프로그래머스 문제 - 트리 트리오 중간값

프로그래머스 트리 트리오 중간값 문제 풀이를 진행하였습니다.

문제 해석

문제를 읽으면 아래와 같은 해석이 가능합니다.

n개의 점으로 이루어진 트리가 주어집니다.
두 점 사이의 거리는 두 점을 잇는 간선의 갯수로 정의합니다.
임의의 점 a, b, c에 대한 함수f(a, b, c)의 값은 a와 b 사이의 거리, b와 c 사이의 거리, c와 a 사이의 거리값의 중간값으로 정의합니다.
(즉, 3개의 값 중 2번째의 값이 중간값입니다.
주어진 트리에서 함수f를 돌려 나올 수 있는 값 중 최대값을 찾아야합니다.

문제 풀이

노드와 노드 사이가 가장 먼 노드를 찾는 것이 중요합니다.

두 노드의 거리가 제일 긴 부분이 중간값에 들어간다면 최대값이 나올 수 있을 것입니다.
하지만 찾아봐야 하는 노드는 3개이므로, 중간값이 두 노드의 거리가 제일 긴 부분으로 들어오기 위해서는 두 노드의 거리가 제일 긴 부분이 2개 이상 존재하면 가능해집니다.
만약 두 노드의 거리가 제일 긴 부분이 1개라면 제일 긴 부분은 중간값이 될 수 없지만 거리가 1짧은 부분은 중간값이 가능해지므로 제일 긴 부분의 거리-1이 중간값이 됩니다.

처음에 시작하는 노드는 정해져있지 않기 때문에 트리의 지름을 구하기 위해 임의의 점에서 제일 먼 리프 노드를 찾아야합니다.
시작점으로 할 리프 노드를 찾아준 후 다시 제일 먼 노드를 검색하여 트리의 지름을 구해줍니다

이때 제일 먼 노드가 두 개 이상이라면 시작점과 제일 먼 노드 두개를 가지고 중간값을 구한 값이 중간값의 최대값이므로 바로 return해주면 됩니다.

만약 제일 먼 노드가 한 개라면 현재 시작점에서 반대쪽까지 계산하면 보이지 않는 다른 노드가 보일 수 있습니다.

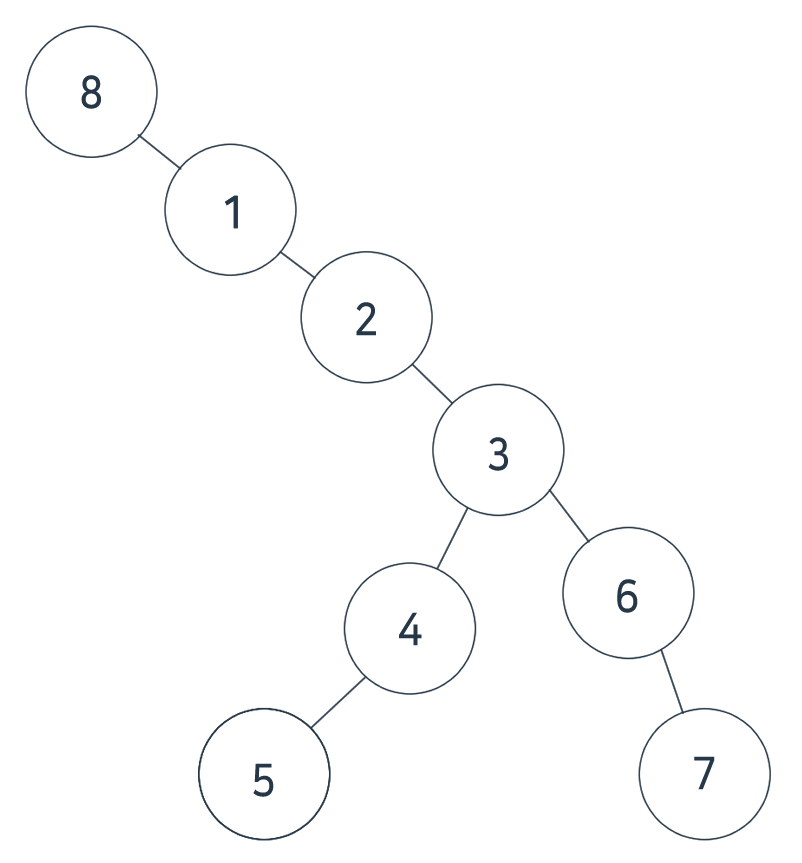
이러한 트리가 주어질 경우를 예를 들면
1번 노드를 시작으로 제일 긴 노드를 검색하면 5와 7이 나옵니다.
둘 다 제일 긴 노드들이기 때문에 한 노드를 선택하여 다시 제일 긴 노드를 검색해줍니다.
5를 시작점으로 검색을 진행하면 8이 제일 긴 노드로 나오게됩니다.
하지만 여기서 한번 더 8을 시작점으로 검색을 진행하면 5와 7이 나오게 됩니다.
즉, 한번 더 검색을 진행함으로써 답이 다르게 나올 수 있습니다.

이러한 반례를 잡기 위해 한번 더 검색을 진행하여 제일 먼 노드가 2개 이상이라면 구한 거리를 return해주면 됩니다.
3번의 검색동안 제일 먼 노드가 1개라면 제일 먼 노드의 자식 노드가 중간값이 되므로, 제일 먼 노드의 거리-1의 값을 return해주면 됩니다.

전체 코드

문제의 반례 때문에 애를 좀 먹었습니다.

#include <bits/stdc++.h>
#include <string>
#include <vector>

using namespace std;

vector<int> tree[250001];
queue<int> lastNode;

int BFS(int n)
{
    int visited[250001] = {0,};
    queue<int> q;
    q.push(n);
    visited[n] = 1;
    int cnt = -1;   //노드의 거리 계산
    while(!q.empty())
    {
        cnt++;
        int qSize = q.size();
        lastNode = q;
        for(int i = 0; i < qSize; i++)
        {
            int curVal = q.front();
            q.pop();
            visited[curVal] = 1;
            for(int val : tree[curVal])
            {
                if(visited[val] == 0)
                {
                    q.push(val);
                    visited[val] = 1;
                }
            }
        }
    }
    return cnt;
}

int solution(int n, vector<vector<int>> edges) {
    int leafNode = 1;
    
    for(vector<int> v : edges)
    {
        tree[v[0]].push_back(v[1]);
        tree[v[1]].push_back(v[0]);
    }
    
    //탐색을 위해 제일 먼 리프 노드 검색
    BFS(1);
    
    //제일 먼 리프 노드를 가지고 제일 먼 노드 다시 검색
    int dist = BFS(lastNode.front());
    //이때 먼 노드가 2개 이상이면 게산한 거리를 return
    if(lastNode.size() > 1)
        return dist;
    
    //제일 먼 리프 노드를 가지고 제일 먼 노드 다시 검색
    dist = BFS(lastNode.front());
    //이때 먼 노드가 2개 이상이면 게산한 거리를 return
    //먼 노드가 1개라면 바로 전 노드가 중간값이 됨
    if(lastNode.size() > 1)
        return dist;
    
    return dist-1;
}

출저

https://school.programmers.co.kr/learn/courses/30/lessons/68937