[Python] 13450: László Babai

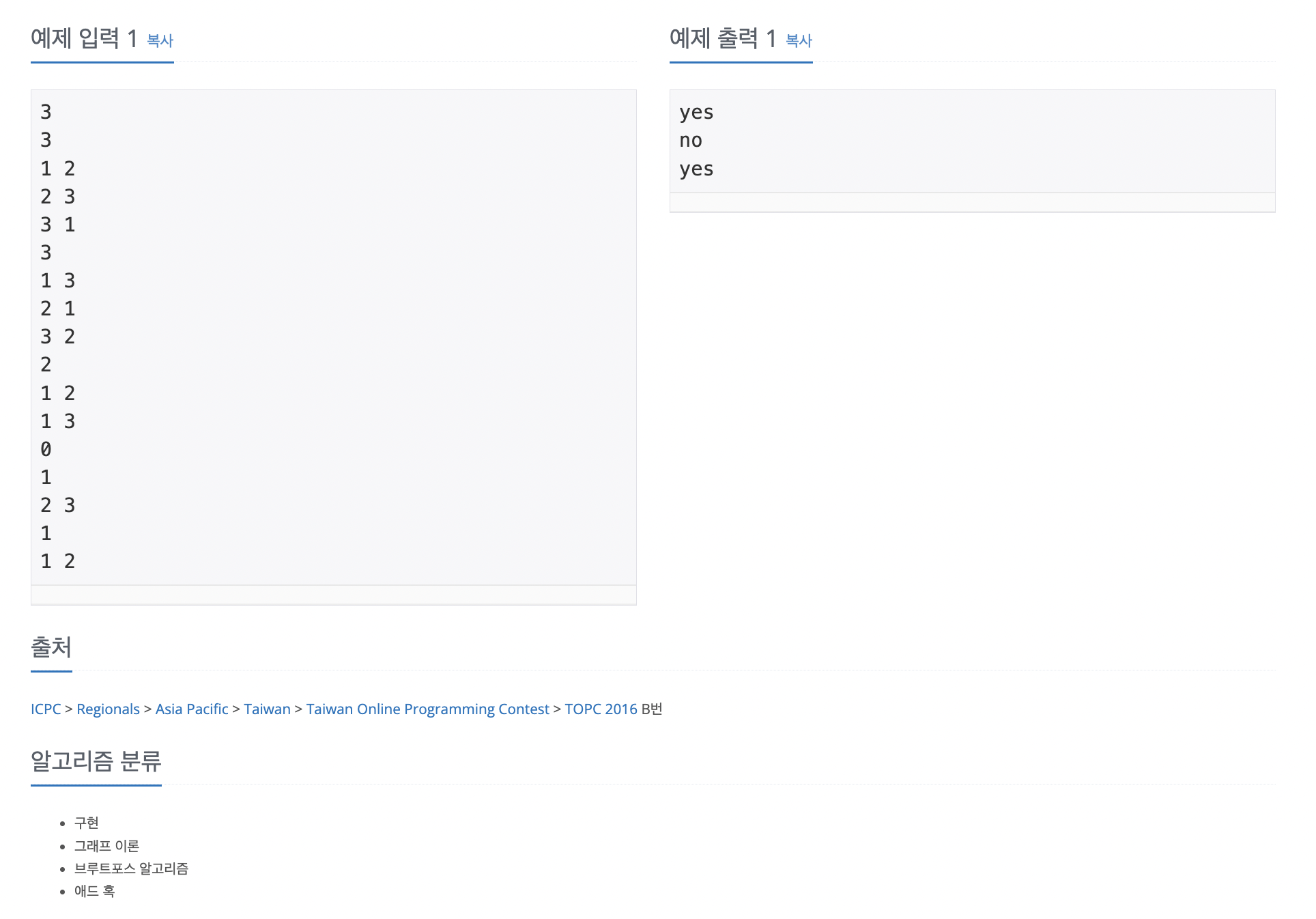
문제 :
Graph isomorphism (동형의 그래프).

방향이 없는 두 개의 그래프
A = (VA, EA) and B = (VB, EB)
A’s vertex set VA = {a1, a2, a3, . . . , anA}
B’s vertex set VB = {b1, b2, b3, . . . , bnB}
가 있을 때,

조건 - Graph A and B are isomorphic if and only if
1. A and B have the same amount of vertices and edges
2. There exists a bijective (one-to-one and onto) function f : VA → VB such that {u, v} ∈ EA if and only if {f(u), f(v)} ∈ EB. (일대일 대응이어야 한다는 것 같음)

그래프는 3개의 vertices (1,2,3)을 가지고 있고,
입력으로는 엣지의 개수와 어느 vertice를 연결하는 엣지인지 받음.

풀이 :

# László Babai (bronze 1)

T = int(input())
results = ['no'] * T

for i in range(T): # 반복문 한 번에 그래프 정보 두 개씩 받음.
    gA = [] # 그래프 A
    gB = [] # 그래프 B

    m = int(input()) # 그래프 A의 에지 개수
    for j in range(m): # 그래프 A의 에지 정보 : v1 v2 를 받음
        uv_set = set(list(map(int, input().split()))) # 집합 (순서가 없음) 에 두 버텍스를 받아서 넣어줌.
        gA.append(uv_set)

    m_ = int(input()) # 그래프 B의 에지 개수
    for j in range(m_):
        uv_set = set(list(map(int, input().split())))
        gB.append(uv_set)

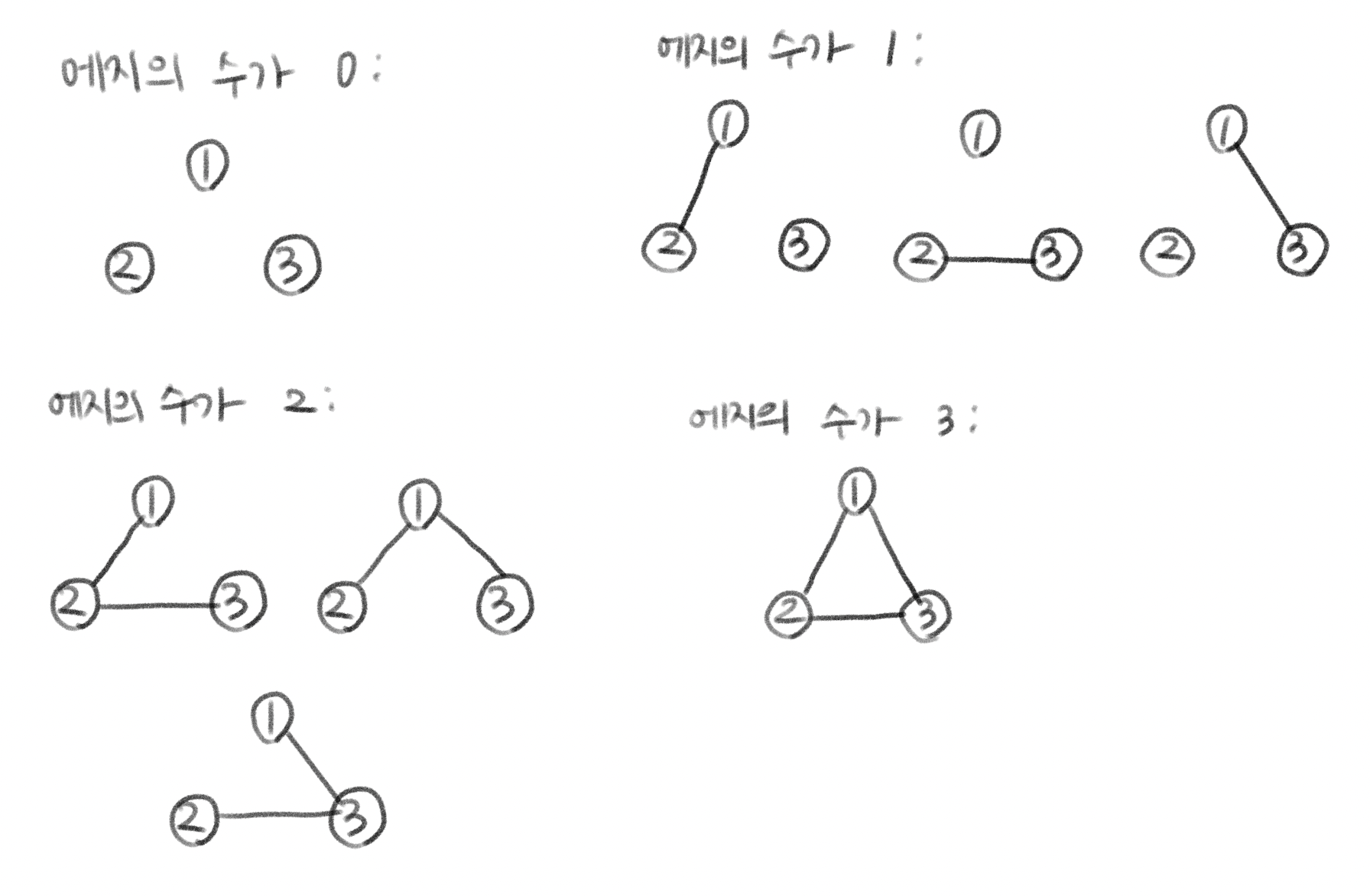
    # vertex는 총 1,2,3 3개뿐이고 
    # 두 버텍스 사이의 에지는 최대 하나만 입력하도록 가정하니,
    # 에지의 수만 같으면 동형의 그래프가 된다.
    if (m == m_): 
        results[i] = 'yes'

for i in range(len(results)):
    print(results[i])

에지의 수만 같으면 동형의 그래프가 되니,
그래프 A와 B의 에지 정보를 받지 않고 그냥 에지 개수 받은 거로만 비교해도 될 듯 하다.
난 일단 에지 정보 받아놓고 어떻게 동형의 그래프로 결정할지 생각하다가 안 거라 그냥 받았음.