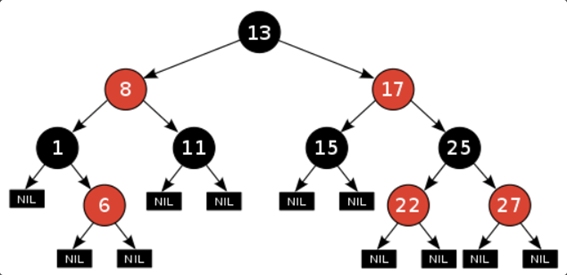
Red-Black Tree는 이진탐색 트리의 문제점을 보완한 트리이다. (따라서 이진트리 기반)
이진탐색 트리 : 부모노드보다 값이 작은 것은 왼쪽 자식, 값이 더 크다면 오른쪽 자식으로 값을 저장한다. (문제점 : 20, 30, 40, 50 순서로 들어온다면 오른쪽으로 치우친 트리가 된다.)
일반적인 이진탐색 트리는 트리의 높이만큼 시간이 필요하므로, 데이터의 삽입이 한쪽으로만 치우치는 경우 트리의 높이가 높아져서 성능이 저하되는 문제가 발생한다.
레드 블랙 트리는 이를 보완하기 위해 정해진 규칙에 따라 트리를 관리하며 트리의 균형을 맞추어 높이를 효율적으로 만들어준다. -> Balanced binary search tree
레드 블랙 트리에는 4가지 규칙이 존재한다.
1. 루트는 블랙이다.
2. 모든 리프(NIL)는 블랙이다.
3. 노드가 레드이면 그 노드의 자식은 반드시 블랙이다.
4. 루트부터 리프노드까지의 블랙 노드의 개수는 같다.
이진탐색 트리는 트리의 높이에 따라 시간복잡도가 좌우되므로 트리의 높이를 균형있게 관리할 수 있다는 것에 따라 레드블랙트리가 현존하는 이진 탐색 트리 중 성능이 가장 좋다고 한다.
-
루트부터 리프까지의 블랙노드의 수가 동일하다는 규칙에 따라 트리의 가장 짧은 높이(모두 블랙노드일 경우)와 가장 긴 높이(블랙-레드의 반복)의 차이는 최대 2배가 안된다는 것이 보장된다.
-
따라서 삽입, 삭제의 경우에도 최선의 상황에서는 O(1), 최악의 상황(아래의 예시)이 오더라도 시간복잡도는 O(logn)으로 좋은 성능을 자랑한다.
-
삽입 시, 삽입되는 노드는 무조건 레드로 삽입된다. 삽입되는 노드의 부모노드가 블랙노드일 경우에는 괜찮지만, 레드노드일 경우에는 3번 규칙에 위배되므로 재배열 또는 색상변경이 필요하다.
이 경우는 부모노드의 형제노드가 블랙인 경우와 레드인 경우에 따라 다르게 처리된다.
<부모노드의 형제노드가 블랙인 경우 - 재배치>
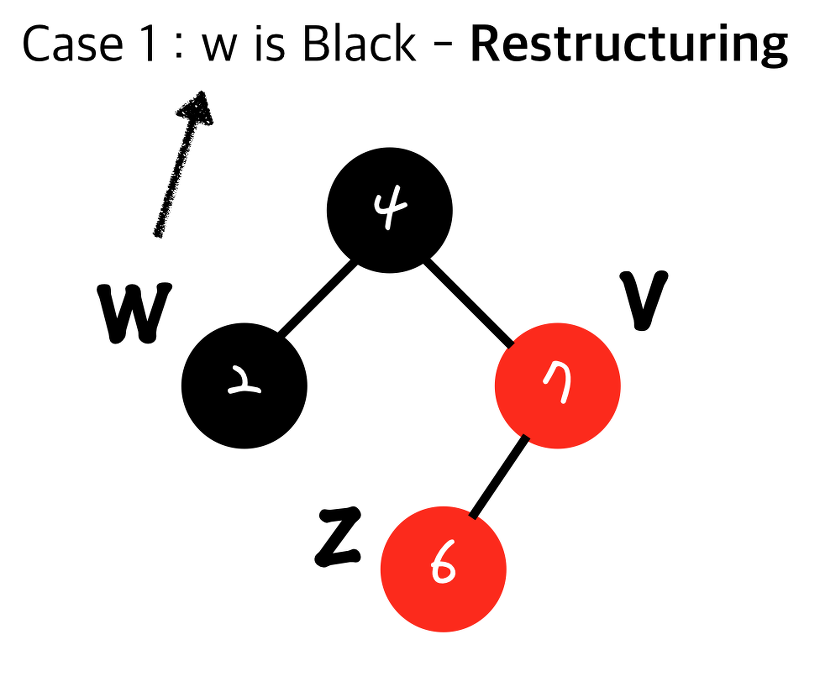
1. 나(삽입노드)와 부모, 부모의 부모 노드 3개를 정렬하여 가운데 값을 부모로 설정한다.
2. 부모로 설정된 노드는 블랙, 자식은 레드로 설정한다.
3. 형제노드인 w노드를 왼쪽아래에 삽입한다.
-> 변환 후에도 블랙노드의 수가 변하지 않기 때문에 한번의 Restructuring으로 해결 가능
Restructuring : O(1), 삽입 : O(logn) 이므로 총 O(logn)의 시간복잡도가 생김
<부모노드의 형제노드가 레드인 경우 - 색상변경>
.png)
1. 나(삽입노드)의 부모와 부모형제 노드를 블랙으로 만들고, 부모의 부모를 레드로 바꿈
- 하지만 부모의 부모가 루트였다면? 1번 규칙이 위배 -> 루트를 블랙으로 변환
- 루트가 아니지만 부모의 부모의 부모가 또 레드라면? 3번 규칙이 위배 -> 다시 Recoloring -> 이것이 루트까지 반복될 수 있음
따라서 Recoloring은 한번으로 끝나지 않을 수 있다.
Recoloring : O(logn), 삽입 : O(logn) 이므로 결과적으로는 O(logn)이 성립된다.