6549번 - 히스토그램에서 가장 큰 직사각형

💡 왜 이거를 stack으로 풀어야 할지 잘 파악하는것이 중요하다. (시간복잡도상 for문을 1번만 돌려서 할 경우 자료구조에 대해서 잘 생각하여 보자!)

import sys

input = sys.stdin.readline

while True:
    
    maxArea = 0
    stack = []
    height = list(map(int,input().rstrip().split(' ')))
    
    if height[0] == 0:
        break
    
    for i in range(1, height[0]+1):
        
        start = i
        
        while stack:
            if stack[-1][0] > height[i]:
                maxArea = max(maxArea, stack[-1][0] * (i - stack[-1][1]))
                # 작은것이 들어오면 제거하면서 출발 인덱스를 바꿔줌 (작은것은 그 왼쪽에도 포함되기 때문에)
                start = stack[-1][1]
                stack.pop()
            else:
                break
            
        stack.append([height[i],start])
    # stack에 남아있는 사각형 넓이 처리
    for h, s in stack:
        maxArea = max(maxArea, h * (height[0]-s+1))

    print(maxArea)   

💡 풀이 방식

• 새로운 것이 stack에 들어올 경우, stack이 비어있으면 [높이, 현재 index]로 넣어준다
• stack이 비어있지 않은 경우, 새로운 것의 높이가 stack의 맨 위의 height보다 크면 그래도 append()해준다.
• stack이 비어있지 않은 경우, 새로운 것의 높이가 stack의 맨 위의 height보다 작으면, stack의 맨위 넓이를 구한다
  => 1. (stack 맨위의 높이) * (현재 index - stack의 맨위의 index)로 높이를 구하고 max 높이 값과 비교한다.
  (stack의 맨위가 자신보다 작은 높이의 것을 만났기 때문에 더이상 가로길이를 확장할 수 없다.)
  => 2. 비교하여 max값을 갱신하고, stack의 맨위를 pop()하고 현재 들어온 작은 높이의 index값을 stack의 맨위의 index값으로 바꿔준다.
  (현재 들어온 것은 stack의 맨위의 값보다 작기 때문에, 넓이를 구할때, 가로길이에 포함될 수 있다.)
  => 3. 위 과정을 stack의 맨 위가 현재 높이보다 작아지기 전까지 or stack이 전부 비어있기 전까지 반복한다.
  => 4. 마지막으로 현재의 높이와 시작 Index를 stack에 넣어준다.
• 위 과정이 모두 끝나고 stack에 남아있는 같은 높이 or 본인보다 작은 것을 바로 만나지 못한 것들의 넓이를 계산하여 최종적으로 max 높이 값과 비교하여 가장 큰 max 높이 값을 도출한다.
  => 해당 높이 * (총 길이 - index)

• 이 문제는 나에게는 꽤 어려운 문제였다.. stack을 이용해서 푸는 방식이라는 것을 알고 접근해도 어려웠다.
• 결국 코딩스터디에서 사람들의 풀이 방식에서 hint를 얻어서 풀 수 있게 되었다.
• 이 문제의 핵심 쟁점은 "시작 index 설정 & 나보다 작은 크기가 나왔을 때 넓이 계산" 이 2가지 였다.

💡 코테 스터디에서 나온 기발한 접근 방식

• 우진님 : 계속 쌓아나가면서 오름차순이 깨지면 그때부터 넓이를 구하면 된다.
  본인보다 작은 값이 나오면, 더이상 너비를 오른쪽으로 확장할 수 없기 때문에, 전부 넓이를 계산하고 max값을 지정하고 stack에서 제거해줘야 한다.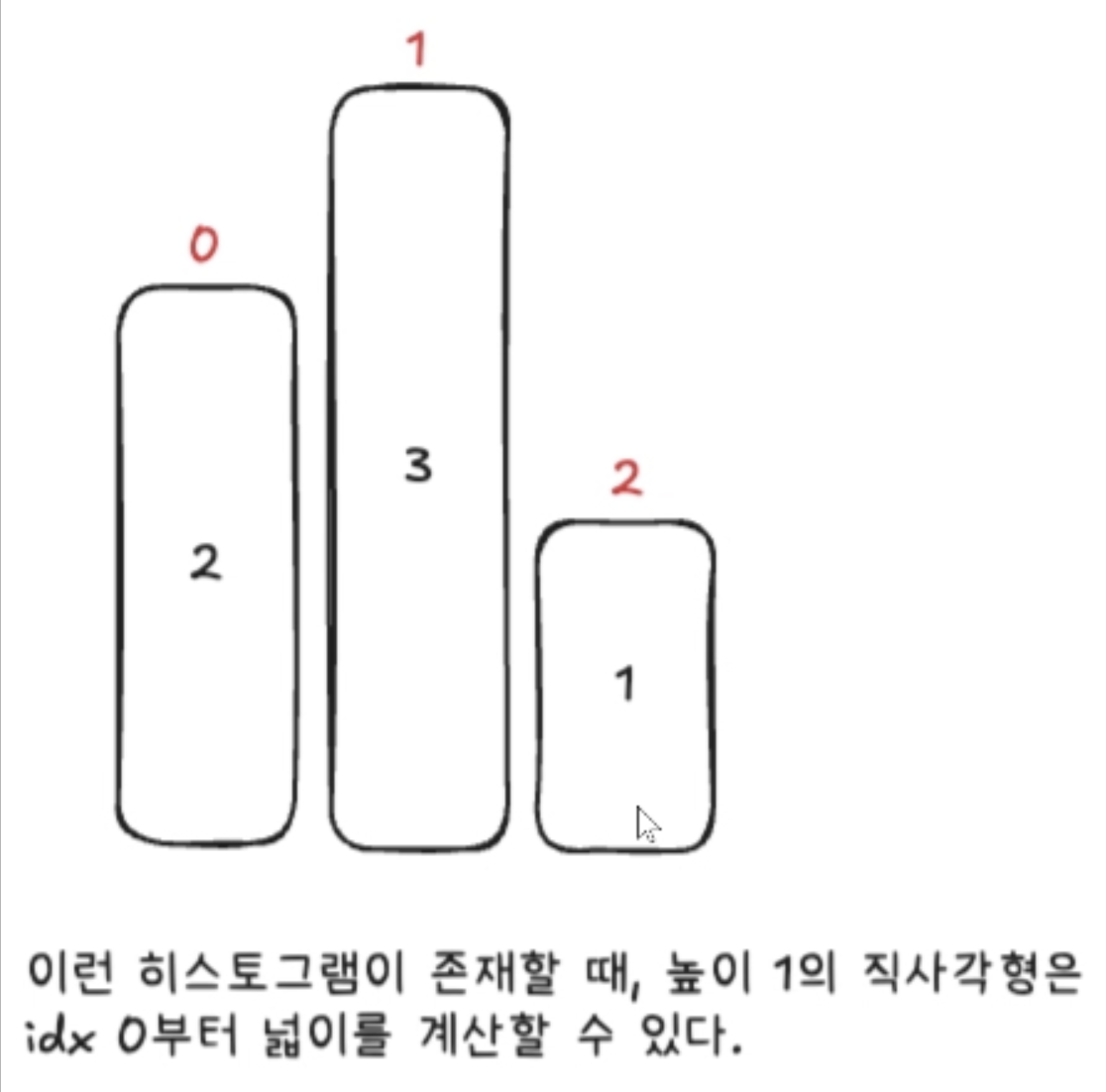

• 서현님: left와 right를 두어서 현재 값의 오른쪽과 왼쪽을 모두 보면서 넓이 값을 비교한다.

LEFT = [0]*N
RIGHT = [N-1]*N

#LEFT
stk=deque()
for i in range(N-1,-1,-1):
    while stk and H[i] < H[stk[-1]]:
        LEFT[stk.pop()]=i+1
    stk.append(i)
#RIGHT
stk = deque()
for i in range(N):
    while stk and H[i] < H[stk[-1]]:
        RIGHT[stk.pop()]=i-1
    stk.append(i)


# print(*LEFT)
# print(*RIGHT)
area = 0
for i in range(N):
    height = H[i]
    width= RIGHT[i]-LEFT[i]+1
    if area<width*height:
        area = width*height
print(area)

• 처음부터 오른쪽 & 왼쪽을 모두 계산하여, 마지막에 stack에 남은것들을 계산하는 연산을 없애고, 완전탐색 형식으로 진행하였습니다.