💡 카카오페이 코테를 준비하기 위해서 알고리즘 정리를 해보고자 한다.

1. 재귀

1. 하나의 함수에서 자기 자신을 다시 호출해 작업을 수행하는 알고리즘
2. 특정 입력에서 자기자신을 호출하지 않고 종료되어야 함
3. 재귀는 코드는 간결하지만, 메모리/시간 측면에서는 손해를 본다 ( 반복문으로만 짜기 너무 복잡한 문제는 재귀로 시도해보자)
4. 재귀에서 자기 자신을 여러번 호출하는 것은 비효율적이다.
5. 재귀함수가 자기 자신을 부를 때 스택 영역에 계속 누적이 된다.

=> Tip:
1. 하나의 함수에 여러 개의 재귀함수를 선언하는 것은 좋지 않다.
2. 재귀는 메모리 초과나 시간초과를 쉽게 발생시킬 수 있으니, 시도해보고 초과가 발생하면 복잡해도 반복문으로 구현해야한다.

2. 백트래킹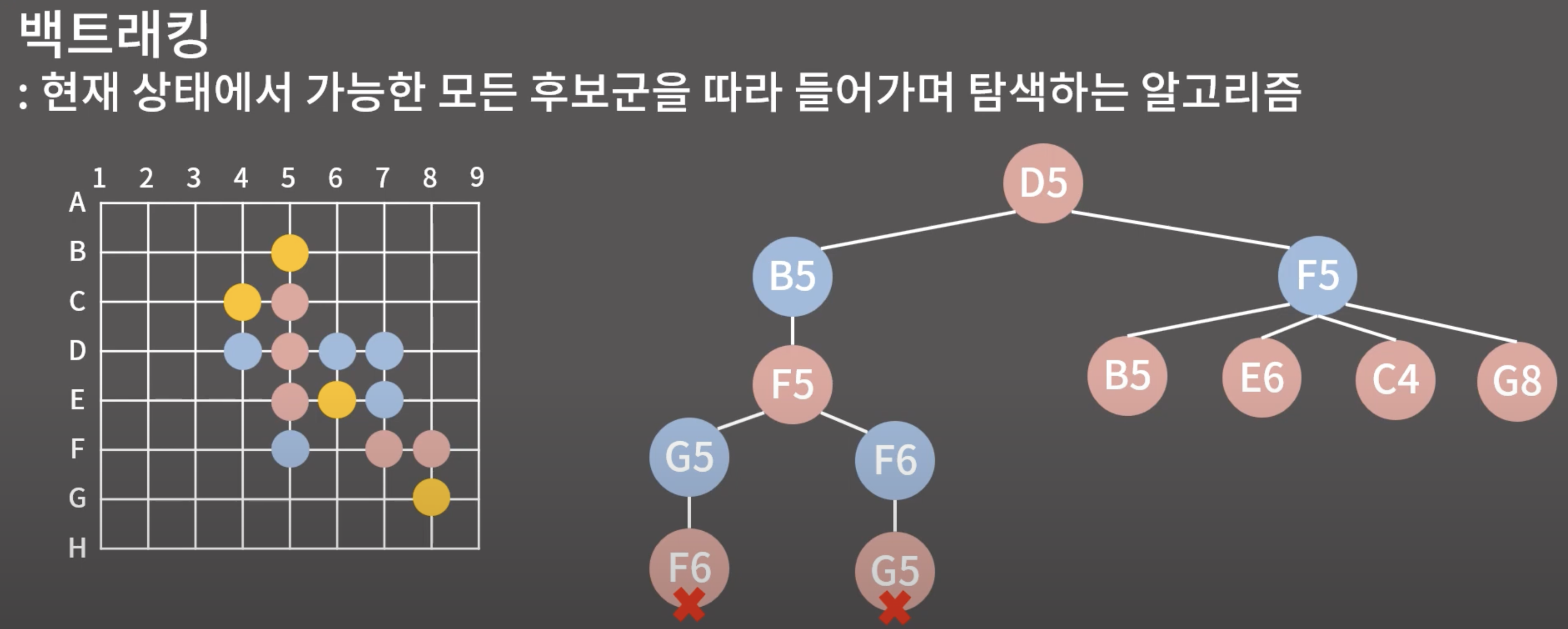

1. 현재 상태에서 가능한 모든 후보군을 따라 들어가며 탐색하는 알고리즘
2. 해당 경로로 갔다가 해당 경로가 맞지 않으면 돌아와서 다른 경로로 가는 방식 사용
3. "상태공간트리"라고도 한다.
4. 재귀를 사용한 알고리즘

=> Tip:
1. 모든 경우의 수를 계산해야 할 때 고려할 필요 있음
2. 입력 크기가 작은 경우 많이 사용
3. 중복없이 선택하는 경우
4. 사전순 (작은수 -> 큰수) 같은 경우 주로 사용

=> 풀이 Top:
1. 조건을 통해 특정 조건에 만족하면 return하는 식으로 재귀를 빠져 나간다
2. 재귀 호출 전 상태 변경 + 재귀 호출 후 상태 복원

3. DP (다이나믹 프로그래밍)

1. 여러 개의 하위 문제를 먼저 푼 후 그 결과를 쌓아올려 주어진 문제를 해결하는 알고리즘
2. 해당 문제의 점화식을 찾아내서 풀어야 한다.
3. 테이블을 만들어야하고, 점화식을 찾아서 초기값을 넣고 점화식에 맞춰서 원하는 값까지 도달하도록 해야한다.
4. 결국 DP는 점화식을 얼마나 빨리 찾냐의 문제이고, 유형을 최대한 많이 익혀야한다.

4. 그리디 (Greedy)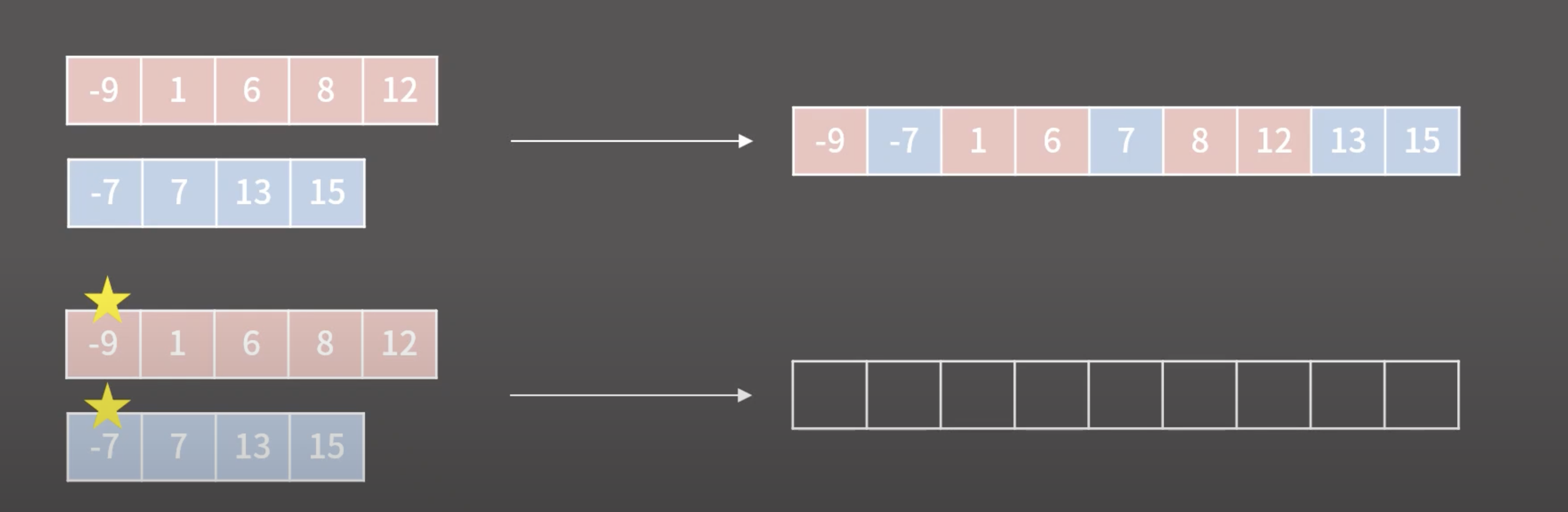

1. 현재 가장 최적인 답을 택하는 알고리즘 ( 그림처럼 현재 상황에 가장 최적인 답을 선택 )
2. 관찰을 통해 탐색 범위를 줄이는 알고리즘
3. 풀이방법
   1) 관찰을 통해 탐색 범위를 줄이는 방법을 생각 (시간 복잡도를 줄일 수 있는 방법을 고안)
   2) 탐색 범위를 줄여도 올바른 결과를 낸다는 것을 확인
   3) 구현을 통한 풀이
4. 풀이 Tip
   => 그리디 풀이 100% 확신 : 짜서 제출해보고 틀리면 바로 손절
   => 그리디 풀이 애매: 다른거 먼저 풀고, 마지막 2-30분 안에 도전
5. 접근 Tip
   => 대부분 그리디 보다는 DP가 많이 나오기 때문에, DP로 풀었는데 시간초과가 발생하거나 한 경우 Greedy를 고려해보자!
   => 가능한 ~~중 가장 먼저 만나는 것 택하기

5. 이분 탐색 (Binary-Search)

1. 정렬 되어 있는 배열에서 특정 데이터를 찾기 위해 탐색 범위를 절반으로 줄여가며 찾는 탐색 방법
2. 선형탐색 : O(N) / 이분 탐색 : O(logN)
3. 파이썬에도 Binary-search를 지원하는 메소드가 존재한다. ( 사용가능하다면 추천)

from bisect import bisect_left, bisect_right

array = [1, 2, 3, 4, 4, 6, 8, 9]
x = 4

print(bisect_left(array, x)) # 3
print(bisect_right(array, x)) # 5

# 특정 값 존재 여부
def count_by_array(a, val):
    right_index = bisect_right(a, val)
    left_index = bisect_left(a, val)
    return right_index - left_index

# 특정 범위 원소 찾기
def count_by_range(a, left, right):
    right_index = bisect_right(a, right)
    left_index = bisect_left(a, left)
    return right_index - left_index


# 특정 갑의 존재 여부 
print(count_by_array(array,3)) # 0보다 크면 존재, 0이면 존재하지 않음


# 특정 범주 내의 존재하는 총 갯수
print(count_by_range(array, -1, 3))
# 특정 값의 갯수
print(count_by_range(array, 4, 4))

• array가 정렬되어 있다면, bisect_left(arr,x)는 arr에서 x가 들어갈 수 있는 가장 왼쪽 인덱스를 반환한다.
• array가 정렬되어 있다면, bisect_right(arr,x)는 arr에서 x가 들어갈 수 있는 가장 오른쪽 인덱스를 반환한다.
• 위 count_by_range함수를 사용해서, 특정 범위내에 포함되는 원소의 개수를 구할 수 있다.
• 위 count_by_range함수를 사용해서 배열 array에서 원소 x의 개수를 구할 수 있다. (left와 right에 동일한 값을 넣어주면 해결)

4. 풀이 Tip
   => 선형 탐색시에 시간복잡도가 터지는 경우에는 고려해봐야한다.
   => 정렬은 필수
   => 파이썬 라이브러리를 사용할 수 있다면 적극 활용 ( But, 해당 배열에 선택값이 존재하는 여부만 알 수 있음)
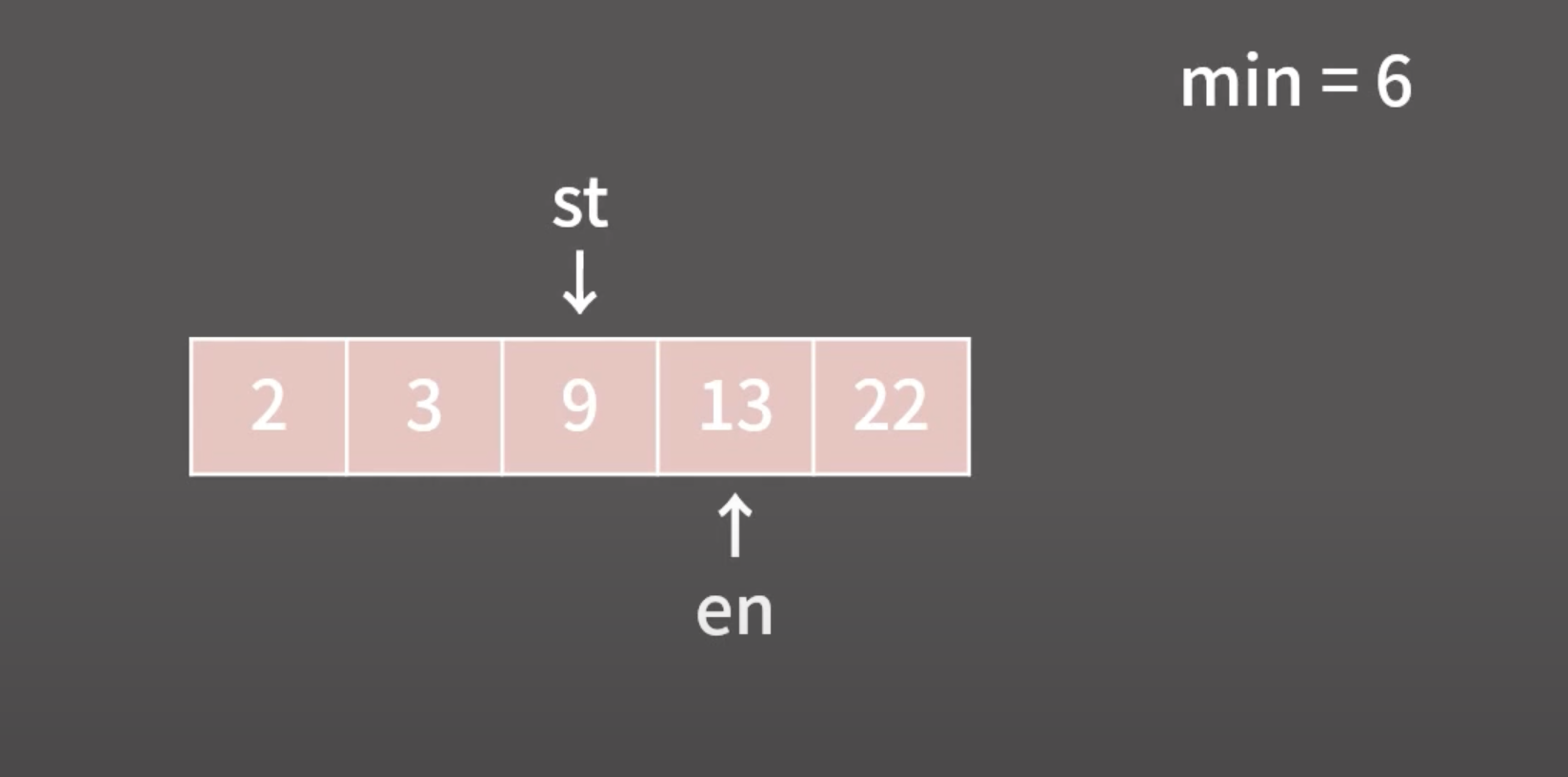
   => start, mid, end를 잘 적용해야하고, 특정상황에 따라 mid값을 구하는 방식이 달라질 수 있음을 주의
   아래와 같이 2가지 경우가 발생할 수 있음. 가끔 1번은 무한루프를 발생시키기도 한다.
   ( 기존 1번 방식때로 진행하였는데 무한루프가 발생한다. 하면 st와 en의 index가 1차이날 경우를 보고 다시 판단하면 된다)
   1) mid = (start + end) / 2
   2) mid = (start+end+1) / 2
   => 유형 고착시키기

# 특정 갯수가 포함되어 있는지
def binary_search(target):
    st = 0
    en = N-1
    
    while(st <= en):
        mid = (st+en)//2
        if target == card[mid]:
        	return True
        elif target < card[mid]:
            en = mid - 1
        else:
            st = mid + 1

## 특정 원소의 갯수 구하기
# 하위 값
def lower_bound(target):
    st = 0
    en = N
    
    while(st < en):
        mid = (st+en)//2
        if target <= card[mid]:
            en = mid
        else:
            st = mid + 1
    
    return st
            
# 상위 값
def upper_bound(target):
    st = 0
    en = N
    
    while(st < en):
        mid = (st+en)//2
        if target < card[mid]:
            en = mid
        else:
            st = mid + 1
    
    return st

5-1. 매개변수 탐색 (Parametric-Search)

1. 조건을 만족하는 최소/최댓값을 구하는 문제(최적화 문제) -> 결정문제로 변환해 이분탐색 수행
   ex) N개를 만들 수 있는 랜선의 최대 길이 (최적화) / 랜선의 길이가 X일때 랜선이 N개 이상인지 여부 (결정)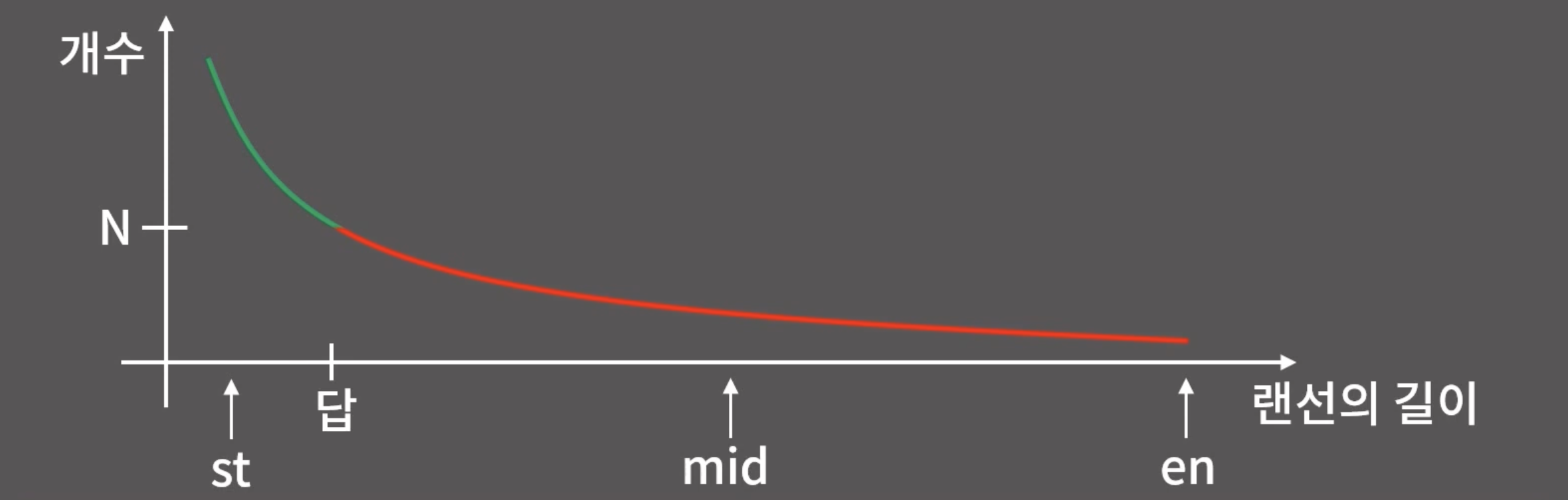

2. 조건은 위와 같은 함수 형태로 나타냈을 때, 증가함수 or 감소함수로 일정해야한다. (뒤죽박죽이면 불가)

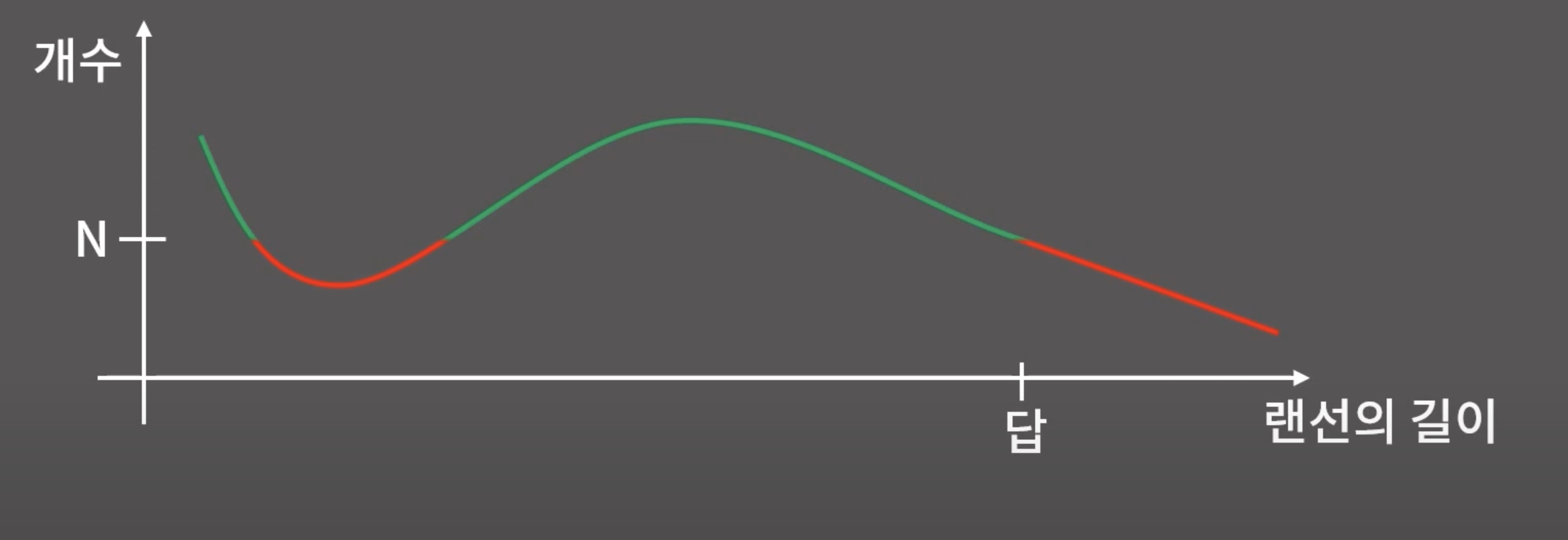
3. 접근 Tip:
   => 최소 or 최대값에 대한 얘기 있을 경우에 범위가 무지막지하게 큰경우
   => 시간 복잡도에게 N하나를 logN으로 떨어트려야 할 경우 고민해봐야 한다. ex) O(N^2) -> O(NlogN)

6. 투포인터

1. 배열에서 이중 For문 (O(n^2))으로 풀어야할 문제를 2개의 포인터를 사용해서 1개의 For문으로 푸는 알고리즘
   
2. 위 방식과 동일하게, 하나의 배열의 for문에서 2개의 포인터가 움직이면서 계산하는 알고리즘이다.
3. 투포인터 -> 이분탐색 / 이분탐색 -> 투포인터 모두 가능하다.
4. 정렬되어 있는 경우 주로 사용

7. 소수구하기 - 에라토스테네스의 체

코딩테스트에서 소수를 구할 경우 많이 사용되는 방식이다.
기존에는 이중 for문을 이용한 O(N^2)의 시간복잡도를 가지고 있지만, 이 경우는 O(N√n )을 가진다.

# 0과 1은 먼저 False 처리
prime = [False,False] + [True] * (N-1)

for i in range(2, int(n**0.5)+1):
	if prime[i]:
    	# i의 배수에 해당하는 수는 전부 False 처리 ( 2,3 등을 제외하기 위해 *2 )
		for j in range(2*i, N+1, i):
        	prime[j] = False

위 방식을 통해 범주를 줄이고, 크기를 키워가면서, 해당하는 수의 배수를 전부 제거해주면 소수인 것 들만 True를 가지고 있다.

8. 우선순위 큐

파이썬에서는 heapq라는 우선순위 큐 라이브러리를 제공한다. (heapq는 Min Heap)
heap은 최소 큐라고도 불리고, 가장 작은 값을 반환하기에 수월하다.(반대로 -를 붙여서 가장 큰 값을 반환하기도 수월하다.)

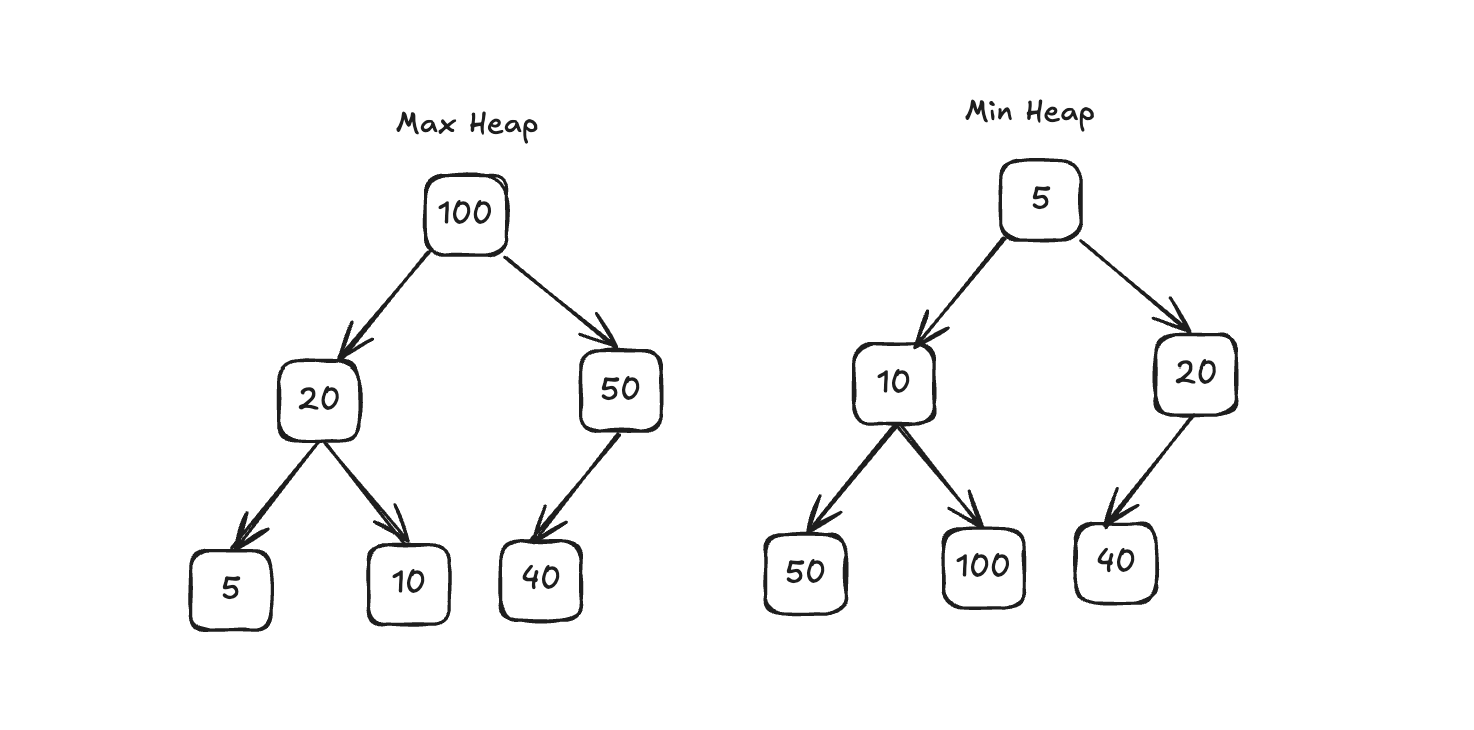
우선순위 큐 (Priority Queue)는 힙(Heap)의 키(Key)를 우선순위로 사용하므로, 우선순위 큐의 구현체가 된다.

Heapq Method

heappush ( 해당 node의 index와 우선순위 같이 넣어줌) - O(logN)
아이템 삽입

heappop - O(lognN)
우선 순위가 가장 높은 or 낮은 노드 삭제

heap[0] - O(1)
우선 순위가 가장 높은 or 낮은 노드 조회

+) 배열을 통해 이진 트리를 구성하고, 부모노드, 자식노드를 찾는법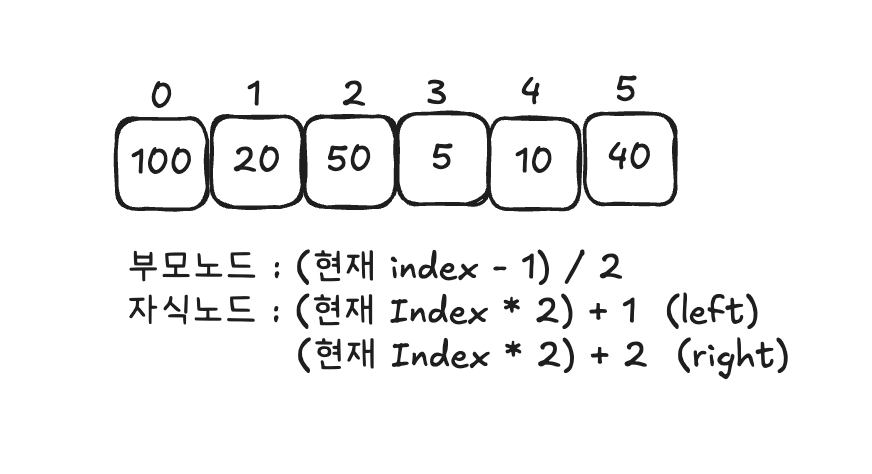

9. 트리(Tree)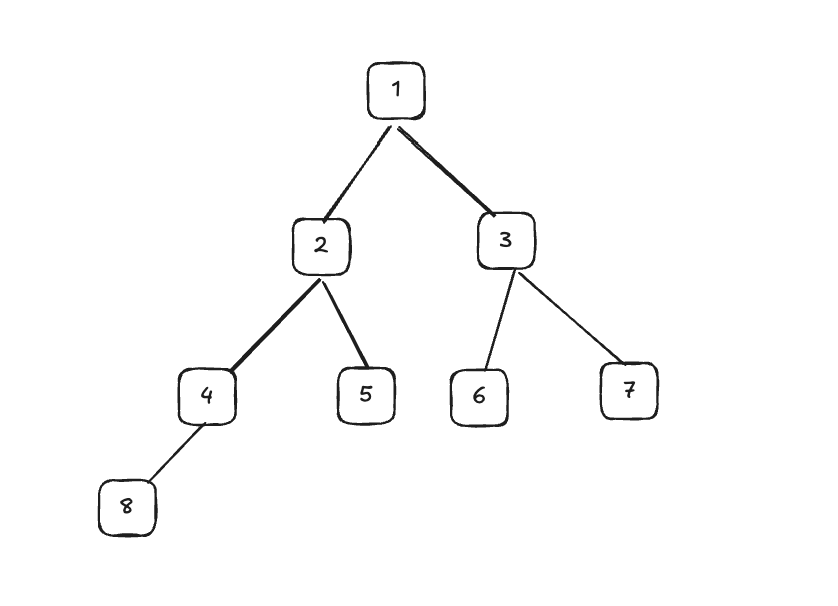

BFS와 DFS는 기존 방식과 동일하게, Deque와 Stack or 재귀를 사용해서 푼다
Tip은 2차원 배열을 통해 1 - 2가 연결되어 있으면 graph[1][2] = graph[2][1] = 1을 통해 저정하거나, graph[1].append(2)를 통해서 각 인덱스와 연결된 노드를 저장해서 풀도록 하자 ( 해당 노드의 부모 노드를 저장할 경우에는 따로 부모배열을 선언하자)

이제, DFS와 BFS를 제외한, 순회에 대해서 알아보도록 하자

1) 레벨순회

레벨순회 = 높이순으로 방문하는 방식 (정점 노드부터 시작)
레벨 순회는 1-2-3-4-5-6-7-8 순으로 순회하며 BFS를 사용하면 자식노드를 넣어주면 해결가능

2) 전위순회

전위순회 = 정점 - 왼쪽 - 오른쪽 순으로 순회한다. (재귀를 사용)
전위 순회는 1-2-4-5-6-3-6-7 순으로 순회하며, DFS를 통해서 해결 가능하다.

3) 중위순회

중위순회 = 왼쪽 - 정점 -오른쪽으로 순회한다. (가장 왼쪽부터 순회)
중위순회는 4-2-5-8-1-6-3-7 순으로 순회한다.

4) 후위순회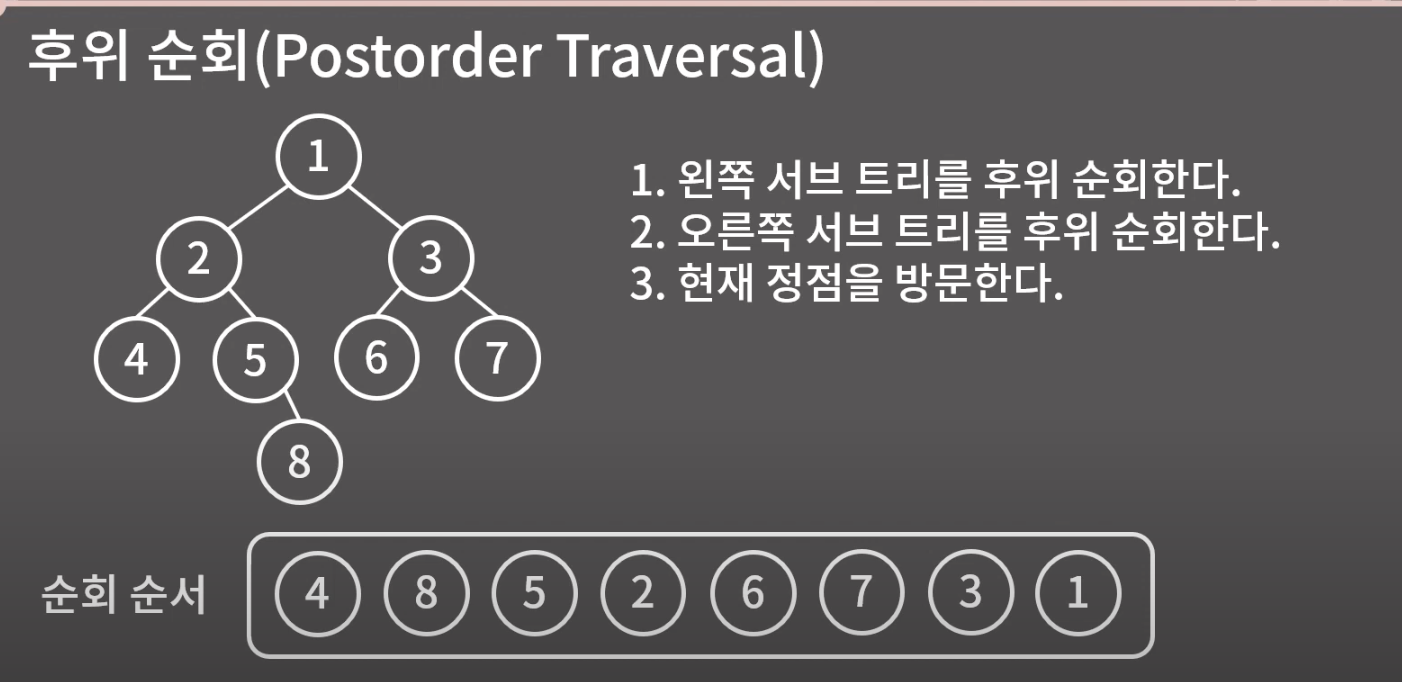

후위순회 = 왼쪽 - 오른쪽 -정점으로 순회한다. (정점보다 오른쪽을 먼저 거침)
후위순회는 4-8-5-2-6-7-3-1 순으로 순회한다.

10. 다익스트라 알고리즘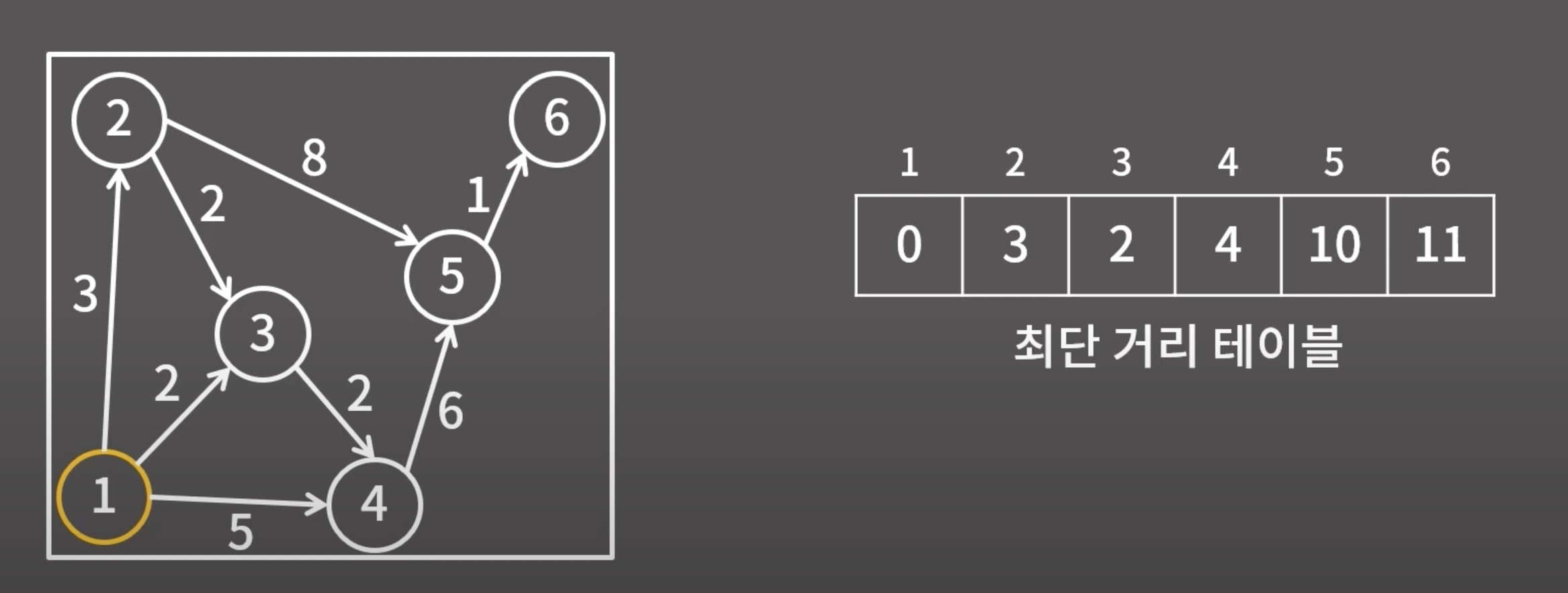

1. 하나의 시작점부터 다른 모든 정점까지의 최단거리를 구하는 알고리즘
2. 최단거리를 구할 때 사용되는 DFS,BFS,DP,Dijkstra 알고리즘 중 하나
3. 간선의 비용이 음수일때는 사용할 수 없다.
4. 최단 거리는 여러 개의 최단거리로 구성되어있다. (DP와 동일)
   ( 하나의 최단거리를 구할 때, 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다.)