[Graph] 3장. Graph Node Embedding Methods

서쿠·2024년 7월 17일
1

GNN 시리즈

목록 보기
3/4
post-thumbnail
post-custom-banner

1. 그래프 노드 임베딩의 필요성

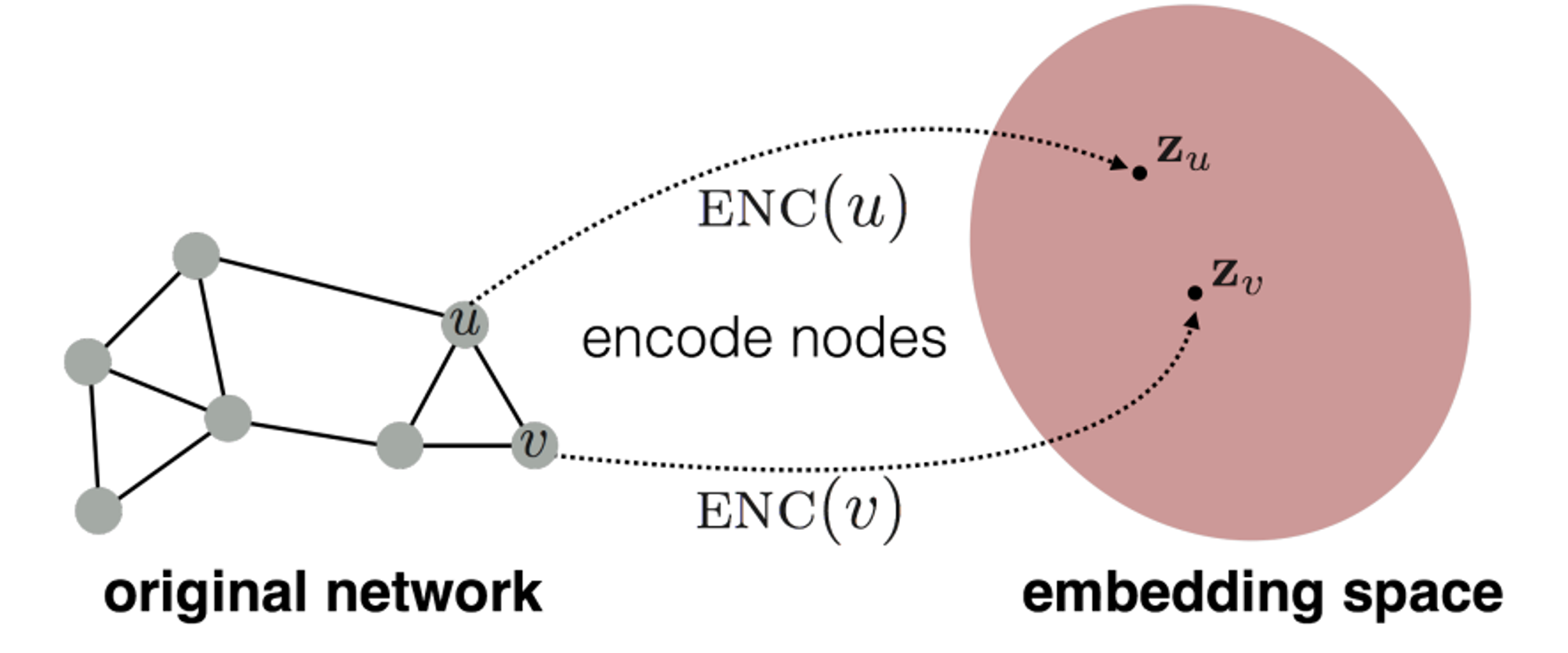
  • 그래프 노드 임베딩은 그래프의 각 노드를 저차원 벡터 공간으로 매핑하는 과정입니다.
    • 이는 그래프 데이터를 기계 학습 알고리즘에 적용하기 쉽게 만들어줍니다.
  • 여기서 중요한 질문은 다음과 같습니다.
    1. 어떤 정보(WHAT)를 우리는 보존(preserve, embed)할 것인가?
    2. 어떻게 정보(HOW)를 정보를 보존할 것인가?
  • 예시:
    • 소셜 네트워크에서 각 사용자를 100차원의 벡터로 표현한다고 가정해봅시다.
    • 이 벡터는 사용자의 특성(나이, 관심사 등)과 네트워크 내 위치(친구 관계, 커뮤니티 등)를 모두 포함할 수 있습니다.

2. 임베딩 과정

  • 임베딩 과정은 크게 네 가지 구성 요소로 이루어집니다:
    1. 매핑 함수: 노드를 벡터로 변환합니다.
    2. 정보 추출기: 그래프에서 보존하고자 하는 핵심 정보를 추출합니다.
    3. 정보 재구성기: 임베딩으로부터 원래 정보를 재구성합니다.
    4. 목적 함수: 추출된 정보와 재구성된 정보의 유사도를 최대화합니다.

3. 변환적(Transductive) vs 귀납적(Inductive) 방법

  • 변환적(Transductive) 방법

    • 정의 :
      • 특정 데이터셋에 대해 직접적으로 예측을 수행하는 방식입니다. 새로운 데이터에 대한 일반화를 목표로 하지 않습니다.
      • 변환적 방법은 학습 시점에 그래프의 전체 구조를 알고 있어야 하며, 모든 노드(학습에 사용되지 않은 노드 포함)에 대한 임베딩을 한 번에 학습합니다.
    • 특징
      • 전체 그래프 구조를 이용하여 학습합니다.
      • 학습 시 보지 않은 새로운 노드에 대해 직접적으로 임베딩을 생성할 수 없습니다.
      • 그래프 구조가 변경되면 전체 모델을 다시 학습해야 합니다.
    • 예시
      • 소셜 네트워크에서 1000명의 사용자에 대한 친구 추천 시스템을 만든다고 가정해봅시다.
        • 변환적 방법은 1000명 전체의 관계를 한 번에 학습하여 각 사용자의 임베딩을 생성합니다.
        • 새로운 사용자가 가입하면, 1001명에 대해 처음부터 다시 학습해야 합니다.
    • 장단점
      • 장점: 전체 그래프 구조를 활용하므로 복잡한 관계를 잘 포착할 수 있습니다.
      • 단점: 새로운 노드 추가 시 계산 비용이 높고, 동적 그래프에 적용하기 어렵습니다.
    • 알고리즘:
      • DeepWalk, Node2Vec

  • 귀납적(Inductive) 방법

    • 정의
      • 일반적인 규칙이나 모델을 학습하여 새로운, 보지 않은 데이터에 적용하는 방식입니다.
      • 귀납적 방법은 노드의 특성과 지역적 이웃 정보를 사용하여 임베딩을 생성하는 규칙을 학습합니다. 이 규칙은 새로운 노드에도 적용할 수 있습니다.
    • 특징
      • 노드의 특성과 지역적 구조를 이용하여 학습합니다.
      • 학습 시 보지 않은 새로운 노드에 대해서도 임베딩을 생성할 수 있습니다.
      • 그래프 구조가 변경되어도 모델을 다시 학습할 필요가 없습니다.
    • 예시
      • 마찬가지로, 소셜 네트워크에서 1000명의 사용자에 대한 친구 추천 시스템을 만든다고 가정해봅시다.
        • 귀납적 방법은 사용자의 프로필 정보와 직접적인 친구 관계만을 이용하여 임베딩 생성 규칙을 학습합니다.
        • 새로운 사용자가 가입하면, 학습된 규칙을 적용하여 즉시 새 사용자의 임베딩을 생성할 수 있습니다.
    • 장단점
      • 장점: 새로운 노드에 대해 유연하게 대응할 수 있으며, 동적 그래프에 적합합니다.
      • 단점: 전체 그래프 구조를 완전히 활용하지 못할 수 있어, 일부 복잡한 관계를 포착하지 못할 수 있습니다.
    • 알고리즘:
      • GraphSAGE

  • 차이점 (inductive vs transductive in graph learning)

    1. 데이터 처리:
      • Transductive: 전체 그래프를 한 번에 처리
      • Inductive: 노드 단위로 처리 가능
    2. 새로운 데이터 처리:
      • Transductive: 새 노드 추가 시 재학습 필요
      • Inductive: 새 노드에 바로 적용 가능
    3. 적용 범위:
      • Transductive: 학습 시 본 그래프에 한정
      • Inductive: 새로운 그래프나 노드에도 적용 가능


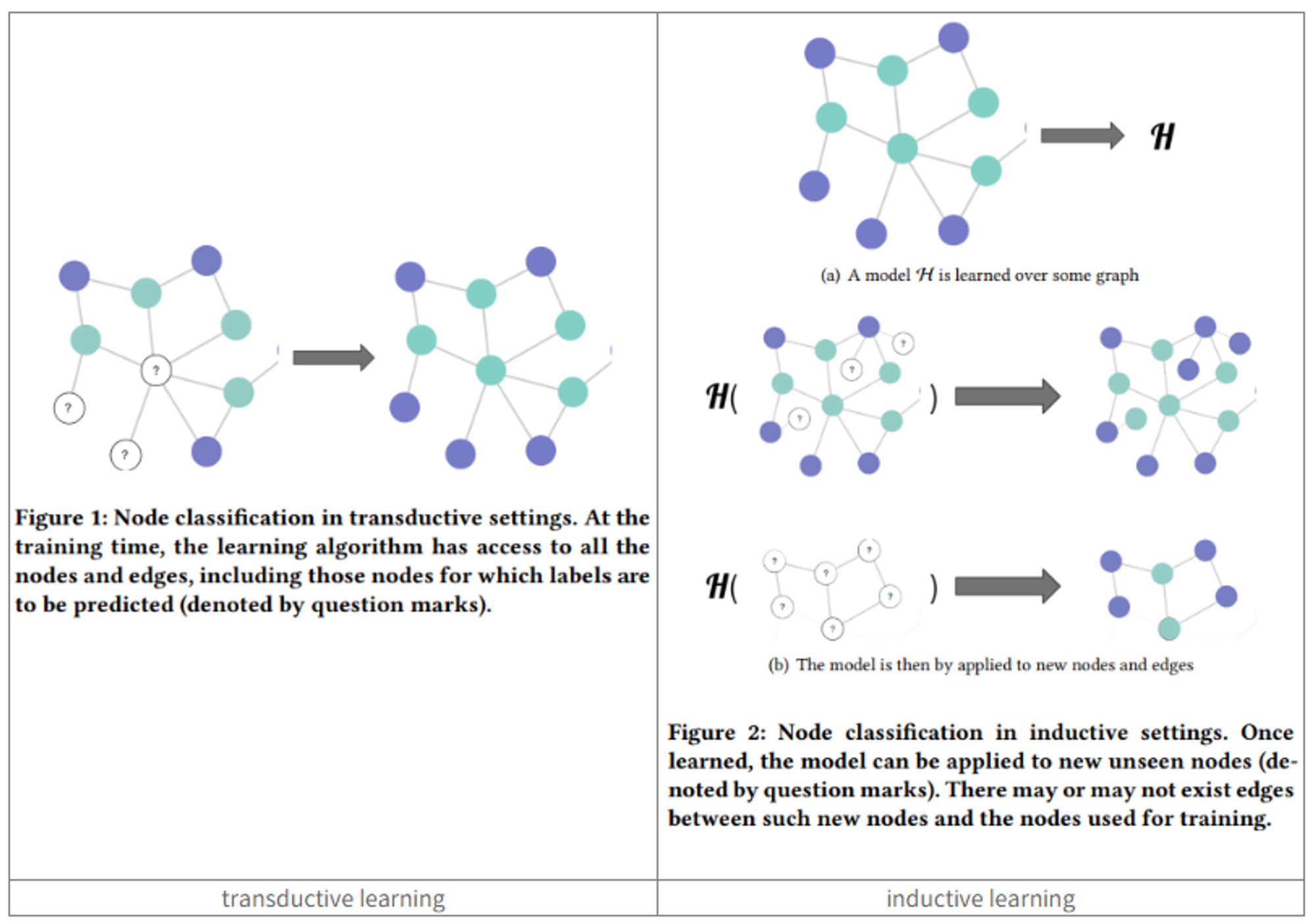
출처: https://data-science-notes.tistory.com/1

  • Transductive Learning (왼쪽 이미지)

    1. 학습 단계:
      • 전체 그래프(모든 노드와 엣지)가 학습 시점에 제공됩니다.
      • 일부 노드(파란색과 청록색)의 레이블은 알려져 있고, 다른 노드(물음표로 표시)의 레이블은 예측해야 합니다.
    2. 예측 단계:
      • 학습된 모델은 학습 시 보았던 그래프의 레이블이 없는 노드(물음표)에 대해 예측을 수행합니다.
      • 새로운 노드나 엣지는 고려되지 않습니다.
    3. 특징:
      • 전체 그래프 구조를 활용하여 학습합니다.
      • 학습 시 보지 않은 새로운 노드에 대해서는 직접적으로 예측할 수 없습니다.

  • Inductive Learning (오른쪽 이미지)

    1. 학습 단계:
      • 모델 H는 일부 그래프에 대해 학습됩니다.
      • 학습된 모델은 노드의 특성과 주변 구조를 이용하여 예측하는 규칙을 학습합니다.
    2. 예측 단계:
      • 학습된 모델은 완전히 새로운 그래프나 노드에 대해 적용될 수 있습니다.
      • 두 가지 예시가 제시됨:
        a) 기존 그래프에 새로운 노드가 추가된 경우
        b) 완전히 새로운 그래프에 적용되는 경우
    3. 특징:
      • 노드의 특성과 지역적 구조를 이용하여 일반화된 규칙을 학습합니다.
      • 학습 시 보지 않은 새로운 노드나 그래프에 대해서도 예측이 가능합니다.

4. DeepWalk 알고리즘

  • DeepWalk 알고리즘은 그래프의 노드를 저차원 벡터 공간으로 임베딩하는 방법입니다.
  • 이 알고리즘의 주요 단계를 슈도 코드로 나타내면 다음과 같습니다:
    • DeepWalk 알고리즘:
      1. 입력: 그래프 G, 워크 길이 l, 워크 수 γ, 윈도우 크기 w, 임베딩 차원 d
      2. 임베딩 벡터 Φ를 랜덤으로 초기화
      3. γ 번 반복:
        • 그래프의 모든 노드 v에 대해:
          • RandomWalk(G, v, l)로 워크 생성
          • SkipGram(Φ, 워크, w)로 임베딩 업데이트
      4. 최종 임베딩 Φ 반환
  • DeepWalk는 다음과 같이 작동합니다:
    • 그래프의 각 노드에서 시작하여 랜덤 워크를 여러 번 수행합니다.
    • 생성된 워크를 문장으로 간주하고, Skip-gram 모델을 사용하여 노드 임베딩을 학습합니다.
    • 이 과정을 통해 그래프의 구조적 정보를 벡터 공간에 인코딩합니다.

(참고) SKIP-GRAM

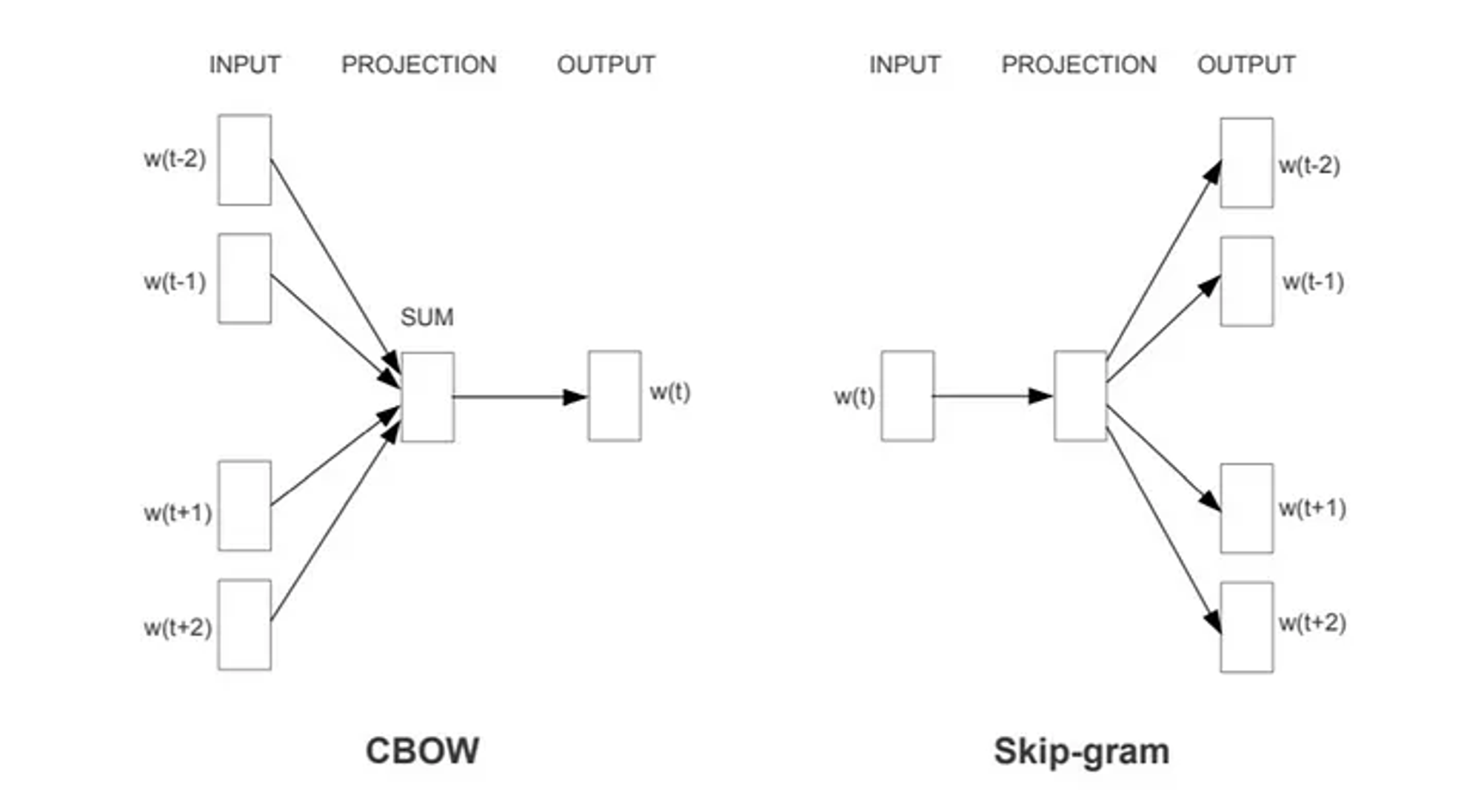
  • SKIPGRAM은 Word2Vec의 한 방법으로, 주어진 단어를 기반으로 주변 단어들을 예측하는 모델입니다. 작동 방식은 다음과 같습니다:

    1. 중심 단어를 입력으로 받습니다.
    2. 은닉층을 통과시켜 임베딩 벡터를 생성합니다.
    3. 이 임베딩 벡터를 사용해 주변 단어들을 예측합니다.
    4. 실제 주변 단어와 예측된 단어 간의 오차를 최소화하도록 학습합니다.

  • DEEPWALK와 SKIPGRAM의 유사점:

    1. 입력 데이터 구조:
      • SKIPGRAM: 문장 내 단어 시퀀스
      • DEEPWALK: 그래프에서 생성된 랜덤 워크 시퀀스두 경우 모두 순서가 있는 시퀀스 데이터를 사용합니다.
    2. 학습 목표:
      • SKIPGRAM: 중심 단어로 주변 단어 예측
      • DEEPWALK: 현재 노드로 주변 노드 예측둘 다 중심 요소를 통해 주변 요소를 예측하는 구조입니다.
    3. 임베딩 생성:
      • 두 방법 모두 저차원 벡터 공간에 요소(단어 또는 노드)를 임베딩합니다.
    4. 컨텍스트 활용:
      • SKIPGRAM: 단어의 주변 컨텍스트 활용
      • DEEPWALK: 노드의 이웃 관계(랜덤 워크로 생성된) 활용
    5. 학습 방식:
      • 두 방법 모두 네거티브 샘플링이나 계층적 소프트맥스를 사용할 수 있습니다.

5. Node2Vec 알고리즘

  • Node2Vec은 DeepWalk를 확장한 알고리즘으로, 더 유연한 무작위 보행 전략을 사용합니다.

    • Node2Vec 알고리즘:
      1. 입력: 그래프 G, 차원 d, 워크 길이 l, 워크 수 r, 컨텍스트 크기 k, 파라미터 p, q
      2. 각 노드 u에 대한 전이 확률 π 계산
      3. 임베딩 벡터 f를 랜덤으로 초기화
      4. r 번 반복:
        • 그래프의 모든 노드 u에 대해:
          • 노드 u에서 시작하는 길이 l의 편향된 랜덤 워크 생성 (π 사용)
      5. 생성된 워크를 사용하여 Skip-gram으로 f 최적화
      6. 최종 임베딩 f 반환

  • Node2Vec은 다음과 같이 작동합니다:

    • DeepWalk와 유사하지만, 랜덤 워크 전략이 더 유연합니다.
      • 파라미터 p와 q를 사용하여 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS) 사이의 균형을 조절합니다.
      • p는 되돌아갈 확률을, q는 멀리 탐색할 확률을 제어합니다.
    • 이를 통해 로컬 및 글로벌 그래프 구조를 더 잘 포착할 수 있습니다.

  • Node2Vec과 DeepWalk의 주요 차이점:

    • 랜덤 워크 전략:
      • DeepWalk: 단순한 무작위 워크를 사용합니다.
      • Node2Vec: 편향된(biased) 랜덤 워크를 사용합니다. 두 개의 파라미터 p와 q를 도입하여 워크의 특성을 조절합니다.
    • 파라미터:
      • DeepWalk: 특별한 파라미터 없이 균일한 확률로 이웃 노드를 선택합니다.
      • Node2Vec: p(돌아올 확률)와 q(멀어질 확률)를 사용하여 워크의 특성을 조절합니다.
    • 그래프 구조 탐색:
      • DeepWalk: 로컬과 글로벌 구조를 균형 있게 탐색합니다.
      • Node2Vec: p와 q 값에 따라 로컬(BFS-like) 또는 글로벌(DFS-like) 구조 탐색을 조절할 수 있습니다.

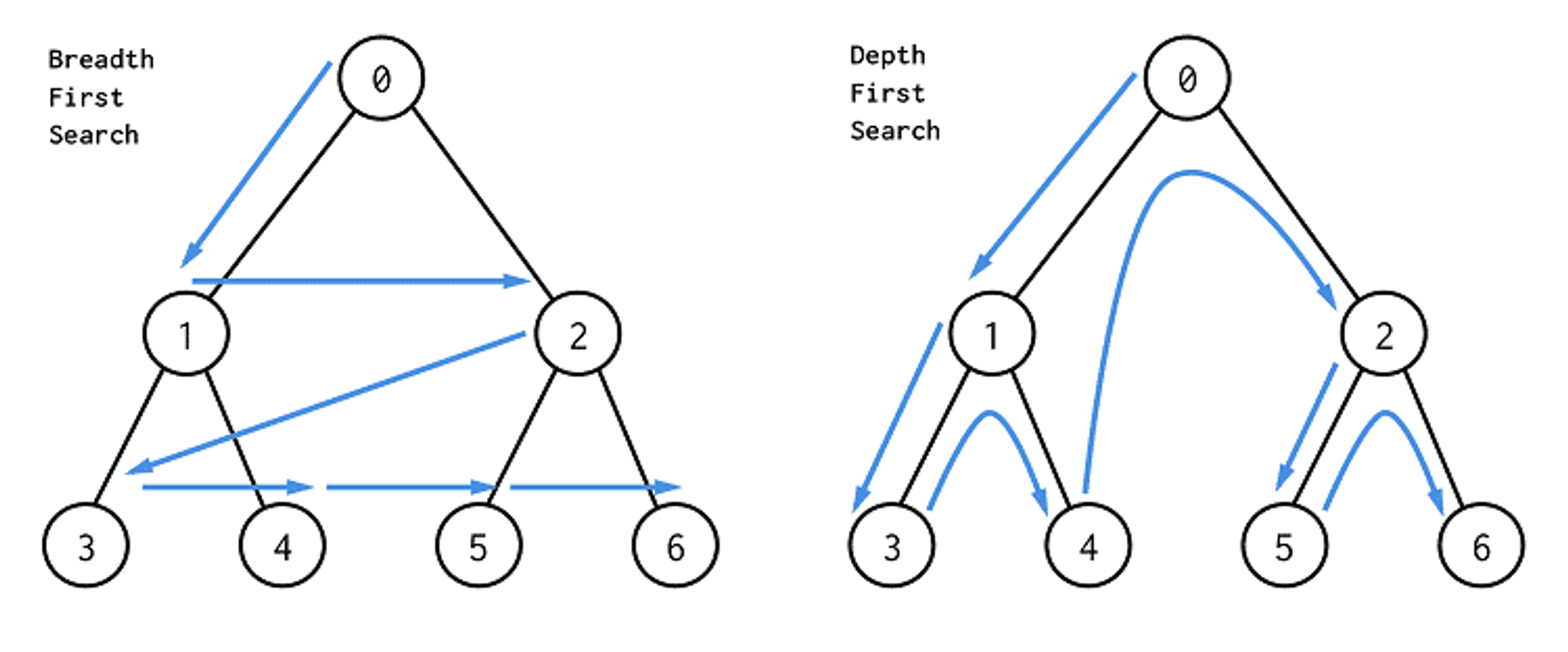
  • Node2Vec과 DFS(BFS)
    • Node2Vec에서 q 값을 낮게 설정하면(q < 1), 워크가 시작 노드로부터 멀어지는 경향이 강해집니다. 이는 DFS(깊이 우선 탐색)와 유사한 동작을 보입니다.
    • DFS는 한 경로를 깊게 탐색하다가 막히면 백트래킹하여 다른 경로를 탐색합니다. Node2Vec에서 q를 낮게 설정하면 현재 노드에서 멀리 있는 노드로 이동할 확률이 높아져, DFS와 유사한 깊이 있는 탐색이 가능해집니다.
    • 반면, q 값을 높게 설정하면(q > 1) BFS(너비 우선 탐색)와 유사한 동작을 보입니다.

6. GraphSAGE 알고리즘

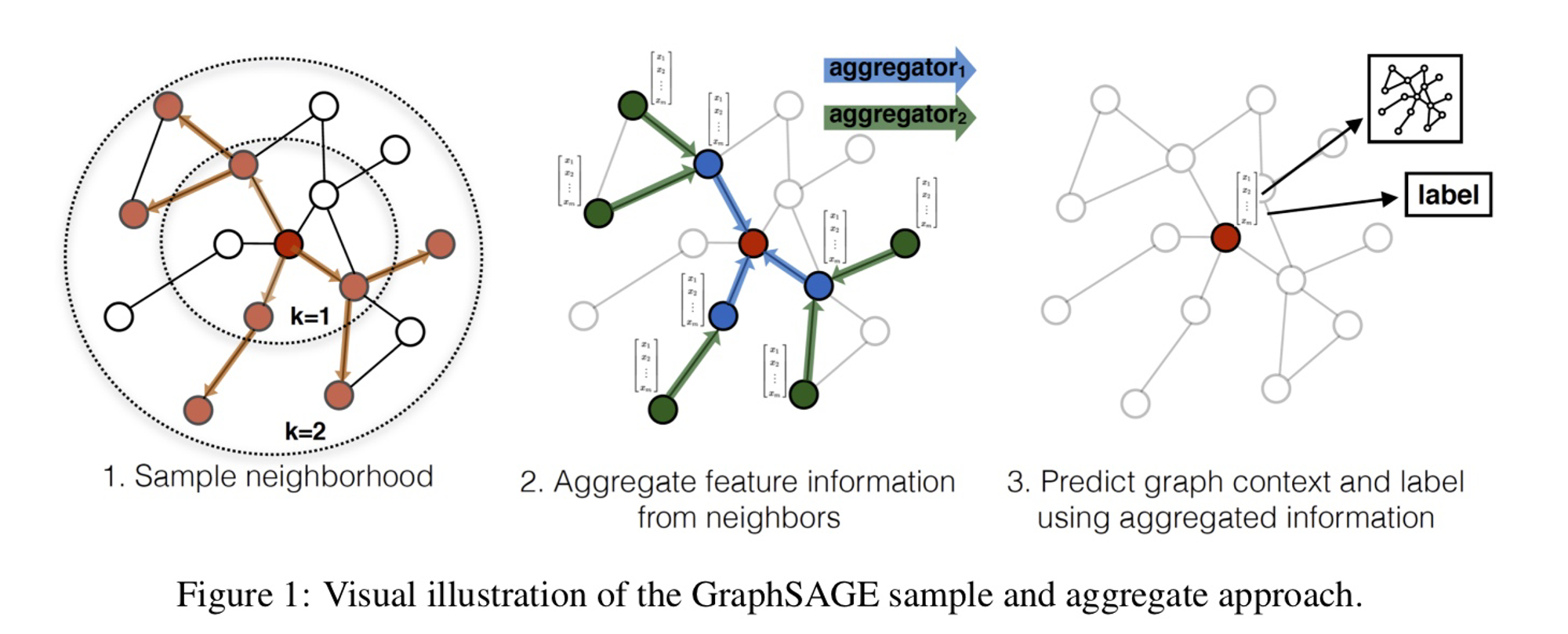
  • GraphSAGE 알고리즘의 슈도코드와 작동 방식은 아래와 같이 정의할 수 있습니다:
    1. 입력:
      • 그래프 G, 노드 특성 X, 깊이 K, 이웃 샘플 크기 S, 가중치 매트릭스 W, 집계 함수 AGGREGATE
    2. 각 노드 v에 대해:
      • hv0=Xvh^0_v = X_v (초기 노드 특성)
    3. For k = 1 to K:
      • 각 노드 v에 대해:
        a. Nv=SampleNeighbors(v,S)N_v = SampleNeighbors(v, S) (v의 이웃 중 S개 샘플링)
        b. hNk=AGGREGATE({huk−1 for u∈Nv})h^k_N = AGGREGATE(\{h^{k-1}_u \text{ for } u \in N_v\}) (이웃 특성 집계)
        c. hvk=σ(Wk⋅CONCAT(hvk−1,hNk))h^k_v = \sigma(W_k \cdot CONCAT(h^{k-1}_v, h^k_N)) (자신과 이웃 특성 결합 후 변환)
    4. 최종 노드 임베딩 반환:
      • zv=hvKz_v = h^K_v
  • GraphSAGE의 작동 방식:
    1. 초기화: 각 노드의 초기 특성을 설정합니다.
    2. 이웃 샘플링: 각 노드에 대해 고정된 수(S)의 이웃을 무작위로 샘플링합니다. 이는 대규모 그래프에서의 계산 효율성을 위한 핵심 단계입니다.
    3. 정보 집계: 샘플링된 이웃의 특성을 AGGREGATE 함수를 사용하여 집계합니다. 이 함수는 평균, 최대값, LSTM 등 다양한 방식으로 구현될 수 있습니다.
    4. 특성 업데이트: 현재 노드의 특성과 집계된 이웃 특성을 결합하고, 가중치 매트릭스를 통해 변환합니다. 이 과정에서 비선형 활성화 함수(σ)를 적용합니다.
    5. 반복: 위 과정을 K번 반복하여 더 넓은 범위의 이웃 정보를 포함시킵니다.
    6. 최종 임베딩: K번의 반복 후, 각 노드의 최종 임베딩을 얻습니다.
  • GraphSAGE의 핵심은 이웃 샘플링과 집계 과정입니다.
  • 이를 통해 대규모 그래프에서도 효율적으로 노드 임베딩을 학습할 수 있으며, 새로운 노드에 대해서도 임베딩을 생성할 수 있는 귀납적 학습이 가능합니다.
profile
서쿠
Always be passionate ✨
이전 포스트

[Graph] 2장. Graph Neural Networks

다음 포스트

[Graph] 4장. Graph Neural Networks: Algorithms

post-custom-banner

0개의 댓글