[머신러닝][차원축소] 변수 선택법

의서쿠·2021년 9월 20일

머신러닝 머신러닝 | 차원축소

본 포스트는 고려대학교 강필성 교수님의 강의를 수강 후 정리를 한 것입니다. 작성 및 설명의 편의를 위해 아래 포스트는 반말로 작성한 점 양해부탁드립니다.

Dimensionality Reduction

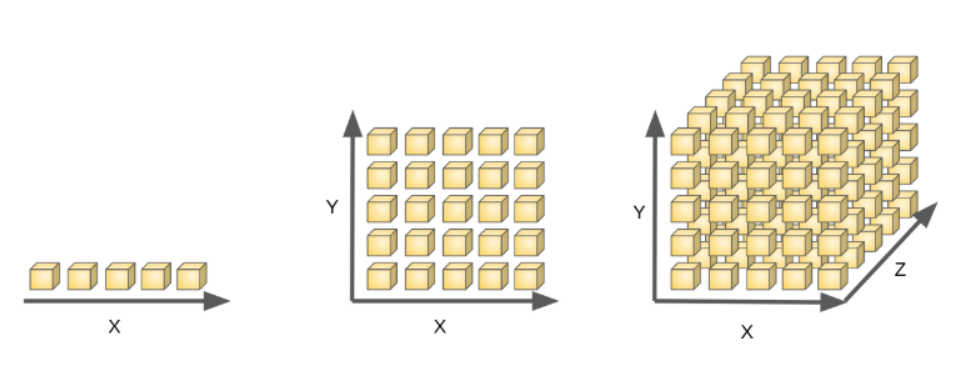
Curse of dimensionality

정의
이론적(theory)으로는 변수의 개수가 증가할 때 모델의 성능도 증가한다. 하지만, 현실(reality)에서는 변수의 개수가 선형적으로 늘어날 때, 동일한 설명력을 갖기 위해 필요한 객체의 수는 지수적으로 증가하며 차원이 너무 커지면 아래와 같은 문제점을 야기한다.
데이터의 변수가 많아질 때의 문제점
① Noise ↑ ② 계산 복잡도 ↑ ③ 동일한 성능을 갖기 위해 필요한 데이터 수 ↑

Dimensionality Reduction

목적
데이터의 본질을 나타내는 내재적 차원(intrinsic dimension)은 실제 차원보다 작다. 따라서, 최적의 변수들의 부분집합(best subset of variables that fit the model)를 찾는 것이 목적이다.
방법
① 도메인 지식을 이용한 변수 선택
② 목적함수에 regularization term 추가
③ 정량적인 차원축소 기법을 수행
영향
① 변수 간의 상관성 제거
② 후처리(post-processing)의 간소화
③ 중복되거나 불필요한 변수 제거
④ 시각화의 용이성
분류 : feed-back loop의 존재에 따라
① Supervised Dimensionality Reduction (지도)
② Un-supervised Dimensionality Reduction (비지도)
분류 : 변수를 선택하는가 추출하는가에 따라
① Variable Feature Selection (변수 선택)
② Variable Feature Extraction (변수 추출)

아래 표는 Dimensionality Reduction (차원 축소)를 위의 분류법에 따라 정리해 본 것이다.

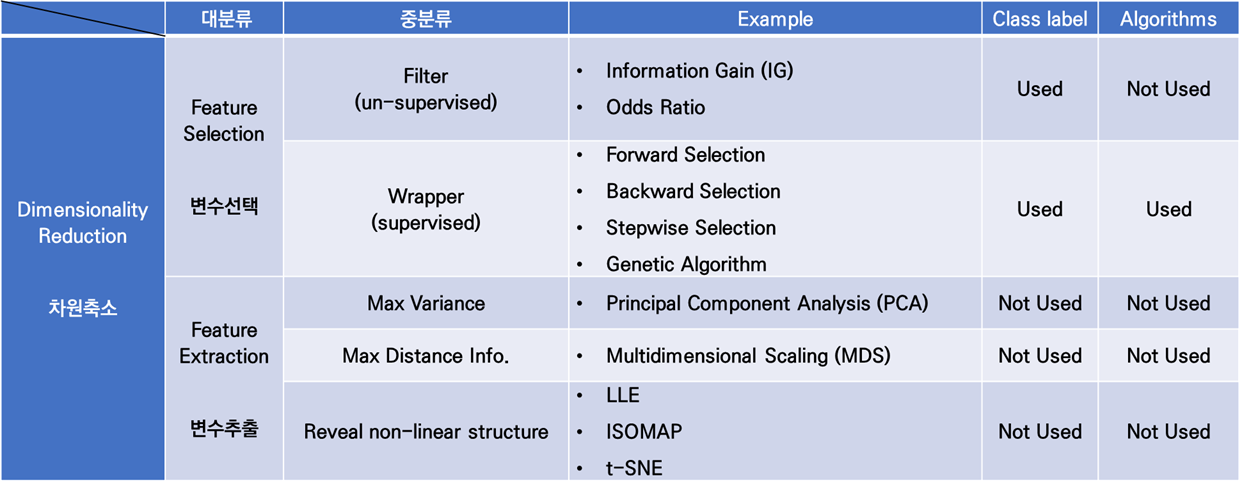
Supervised Variable Selection

제일 첫번째 소개할 방법은 변수 선택 중 Wrapper 기법인 Supervised Variable Selection이다.

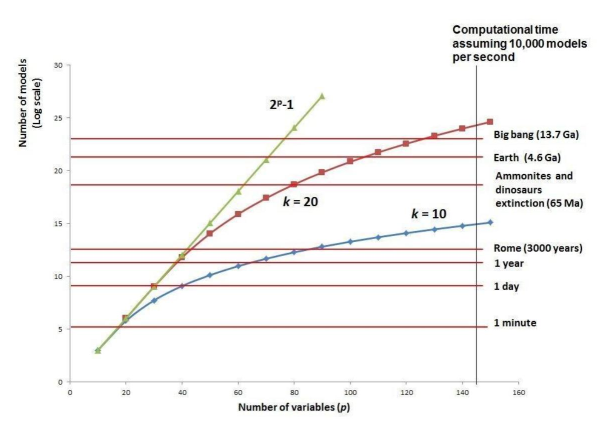
Exhaustive Search

모든 변수의 조합에 대하여 탐색을 수행함. 항상 global optimum 반환하지만 느리다.

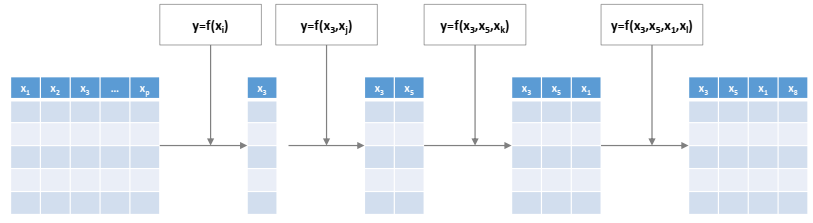
Forward Selection

아무 변수가 없는 것부터, 가장 유의한 변수들을 하나씩 순차적으로 추가하며 탐색을 수행함 (이때, 한번 추가된 변수는 제거되지 않는다.)

Backward Elimination

모든 변수가 다 있는 것부터 불필요한 변수들을 하나씩 순차적으로 제거해가며 탐색을 수행함 (이때, 한번 제거된 변수는 다시 추가되지 않는다.)

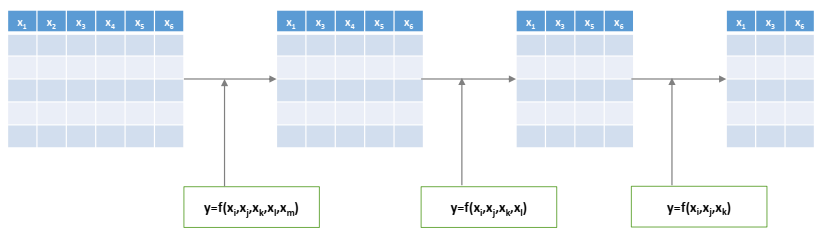
Stepwise Selection

아무 변수가 없는 것부터, Forward Selection과 Backward Elimination을 번갈아 가며 수행함 (이때, 변수가 한번 선택 또는 제거가 되었을지라도, 다음 번에 다시 뽑히거나 제거될 수 있다.)

사용될 수 있는 Performance Metric로는 아래와 같은 기법들이 사용될 수 있다.

Akaike Information Criteria (AIC)

AIC=n \cdot \ln \left(\frac{S S E}{n}\right)+2 k

Bayesian Information Criteria (BIC)

B I C=n \cdot \ln \left(\frac{S S E}{n}\right)+\frac{2(k+2) n \sigma^{2}}{S S E}-\frac{2 n^{2} \sigma^{4}}{S S E^{2}}

Adjusted R2

\text { Adjusted } R^{2}=1-\left(\frac{n-1}{n-k-1}\right)\left(1-R^{2}\right)=1-\frac{n-1}{n-k-1} \frac{S S E}{S S T}

참고로, 여기서 나오는 SST와 SSA는 회귀분석 분석 시에 자주 쓰이는 Term으로 아래와 같이 정의된다.

SST = SSR + SSE

$where$ ,
$SST = sum　of　squares　of　total$
$SSR = sum　of　squares　of　regression$
$SSE = sum　of　squares　of　errors$

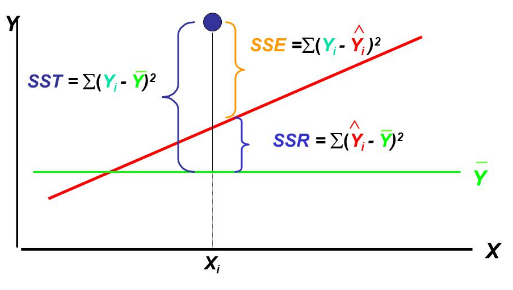
Genetic Algorithm

앞에서 소개한 Exhaustive Search과 Local Search은 다음과 같은 단점이 존재한다.

① Exhaustive Search : 데이터를 제일 잘 설명할 수 있는 최적의 부분집합을 찾아낼 수 있지만, 이를 찾는 데까지 오랜 시간이 걸린다.
② Local Search (forward/backward/stepwise) : 효과적으로 찾는 방법이지만, search space가 제한적이라서 최적해가 아닌 해를 찾게 될 수 있다.

위에 소개한 기법들의 문제가 없으며 "모델의 “성능” 과 “속도” 를 모두 올릴 수 있는 방법이 있을까?"라는 질문을 해결하기 위해 자연현상을 본 따 제안된 것이 바로 Meta-Heuristic Approach이다.

ex) ANN(인간의 뇌), Ant Colony Algorithm(개미 군집), Particle Swarm Optimization(입자 군집)

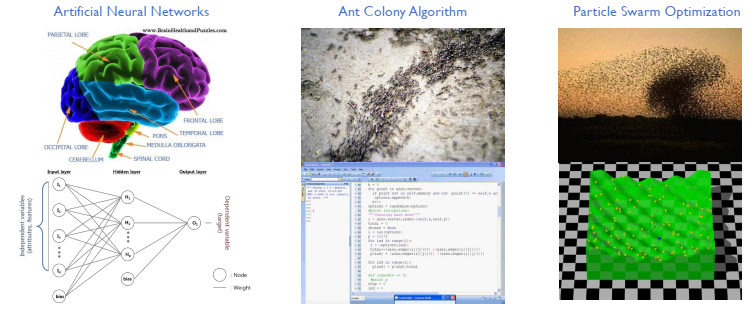
Genetic Algorithm 역시 이와 같은 Meta-Heuristic Approach 중 하나로, “자연선택설” + “생식(유전) 프로세스” 를 모방한 방법이다.

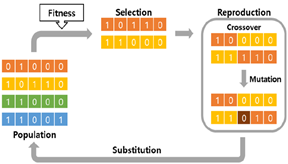
위의 그림은 Genetic Algorithm(GA)의 Process이며, GA는 크게 아래와 같이 3가지 프로세스로 구성되어 있다:

① Selection(선택) : 품질(quality)를 올리기 위해 우월한 유전자(solution)을 선택
② Crossover(교배) : 현재 선택된 유전자들(solution) 간의 교배를 통해 대안을 탐색
③ Mutation(돌연변이) : local optimum(국소 최적)에서 나갈 수 있도록 변이(mutation)를 더함

아래는 우리가 알고 있는 염색체(Chromosome) 그림이다. 염색체는 매우 긴 가닥의 DNA로 구성되며 많은 유전자(Gene)가 들어 있다(수백 개에서 수천 개).

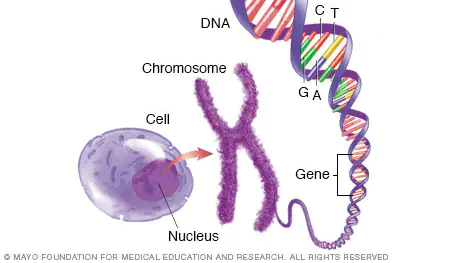
변수 선택법으로써 쓰이는 GA에서 염색체(Chromosome)은 변수의 집합, 유전자(Gene)은 하나의 변수를 의미한다. 아래 그림은 이를 표현해본 것이다.

아래는 GA를 이용한 변수 선택법의 프로세스와 용어 설명은 아래와 같다.

Population Size: 사용할 염색체의 수
Fitness Function: 염색체 퀄리티 평가 기준(AIC, BIC, R2)
- 두 염색체가 같은 성능(performance)를 보이면 변수의 수가 적은 것이 good
- 두 염색체의 변수의 개수가 같으면 좀 더 좋은 성능을 보이는 염색체가 good
Selection Mechanism: 우수한 염색체(superior chromosome)를 선택하는 방식
- deterministic selection: 상위 N%만 채택하고, 하위 (100-N)%는 폐기한다.
- probabilistic selection: performance를 기준으로 선택 가중치(selection weight) 정의 후 확률적으로 염색체를 선택한다.
Crossover Mechanism: 교배(교차) 방식
- crossover point: 교차가 몇 번 일어날 지 정해준다. 난수 생성 후 cut-off를 넘으면 crossover을 하도록 지정이 가능하다.
Rate of Mutation : 돌연변이율
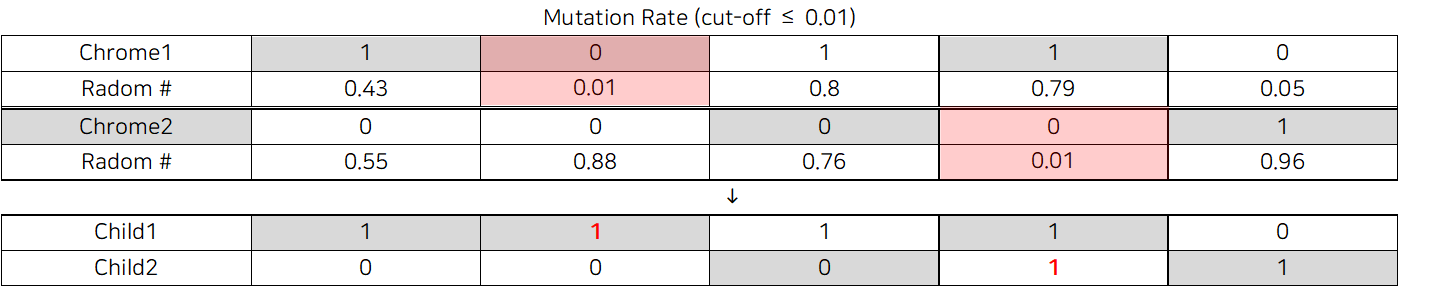
- 난수 생성 후 돌연변이율보다 낮은 값은 mutation을 수행한다.
iteration: 세대 반복 횟수
- 한 세대는 학습에 이용될 염색체 선택부터 다음 세대에 염색체 생성까지의 단계를 일컫는다.
- 안전장치로서, 이전 세대의 best 염색체들을 다음 세대에 가져와서 함께 이용하기도 한다. 성능이 감소되지 않도록 하는 역할을 수행한다. (만일 더 좋은 자식 세대가 나오면 best가 교체되고, 그렇지 않으면 현재 best 값에 수렴하게 하는 역할)
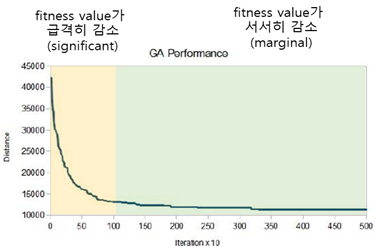
Stopping Criteria: 학습 종료조건