[Algorithm] 99클럽 코테 스터디 22일차 TIL BOJ 11053

문제

https://www.acmicpc.net/problem/11053

풀이

문제 분석

• 수열이라고하여 등차/등비를 생각하게 되었는데, 코드가 너무 복잡하여 최장 증가 수열의 정의를 찾아보게 되었다
• 정의를 확인하니 단순히 숫자가 증가하는 양상이면 최장 증가 수열이라는 것을 확인할 수 있었고, 이를 바탕으로 이중 for문을 돌며 자신보다 작은 숫자의 length에 1을 더해 자신의 길이를 업데이트하는 방식으로 문제를 해결했다
• 대부분의 사람들은 이 length를 구하는 과정을 dp라고 생각하여 배열 이름도 dp로 많이 지은 것 같았다

코드

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int max = 1;
        int[] numbers = new int[N];
        int[] length = new int[N];
        st = new StringTokenizer(br.readLine());
        for(int i=0 ; i<N ; i++) {
            numbers[i] = Integer.parseInt(st.nextToken());
        }

        for (int i = 0; i < N; i++){
            length[i] = 1;
            for (int j = 0; j < i; j++){
                if(numbers[j] < numbers[i]){
                    length[i] = Math.max(length[i], length[j] + 1);
                }
            }
            max = Math.max(length[i], max);
        }

        bw.write(String.valueOf(max));
        bw.flush();
        bw.close();
    }
}

TIL

• 다이나믹 프로그래밍에 대해 정리해보려 한다

LIS(Longest Increasing Subsequence)

• 최장 증가 부분 수열: 어떠한 수열에서 오름차순으로 증가하는 가장 긴 부분수열을 의미한다
• 이 때, 부분 수열의 각 수는 서로 연속할 필요는 없다

위 수열에서 최장 증가 수열을 찾으면 아래와 같다

주어진 수열에서 LIS의 길이를 구하는 방법은 2가지이다

다이나믹 프로그래밍을 이용한 방법: O(N^2)

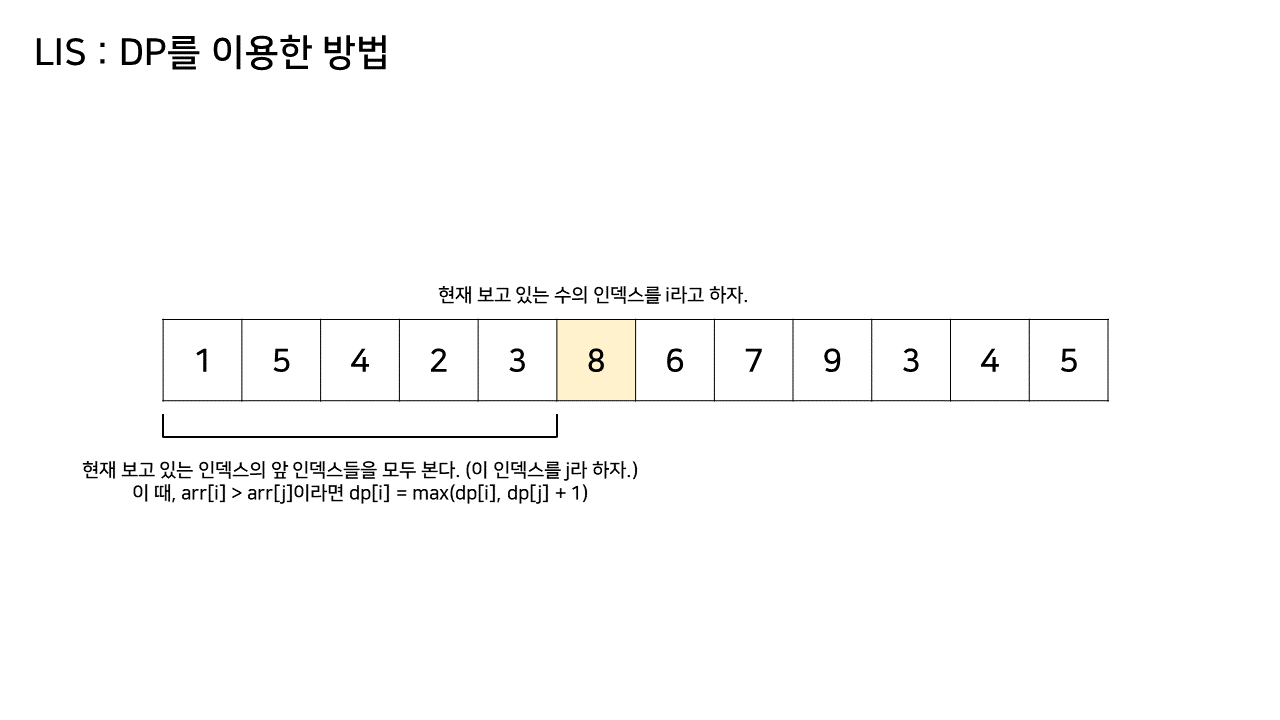
• 수열의 한 원소에 대해, 그 원소에서 끝나는 최장 증가 수열을 생각해보면 그 최장 증가 수열의 k를 제외한 모든 원소들은 반드시 k보다 작아야 한다
• 따라서 k의 앞 순서에 있는 모든 원소들 중 값이 k보다 작은 원소에 대해, 그 각각의 원소에서 끝나는 최장 증가 수열의 길이를 알고 있다면, k에서 끝나는 최장 증가 수열의 길이도 구할 수 있을 것이다
• dp[i] : i번째 인덱스에서 끝나는 최장 증가 수열의 길이 로 정의한다
• 코드

void LIS_DP() {
    for (int i = 0; i < n; i++) {
        dp[i] = 1; // 자기 자신의 최장 증가 수열의 크기를 1로 설정
        for (int j = 0; j < i; j++) {
            //i번째 이전의 모든 원소에 대해, 그 원소에서 끝나는 LIS의 길이를 확인한다.
            if (arr[i] > arr[j]) {
                //단, 이는 현재 수가 그 원소보다 클 때만 확인한다.
                dp[i] = max(dp[i], dp[j] + 1);        //dp[j] + 1 : 이전 원소에서 끝나는 LIS에 현재 수를 붙인 새 LIS 길이
            }
        }
    }
}

이분 탐색을 이용한 방법: O(NlogN)

• 이분 탐색을 사용하면 시간 복잡도를 O(NlogN)으로 줄일 수 있다
• LIS를 기록하는 배열을 하나 더 두고, 원래 수열에서 각 원소에 대해 LIS 배열 내에서의 위치를 찾는다

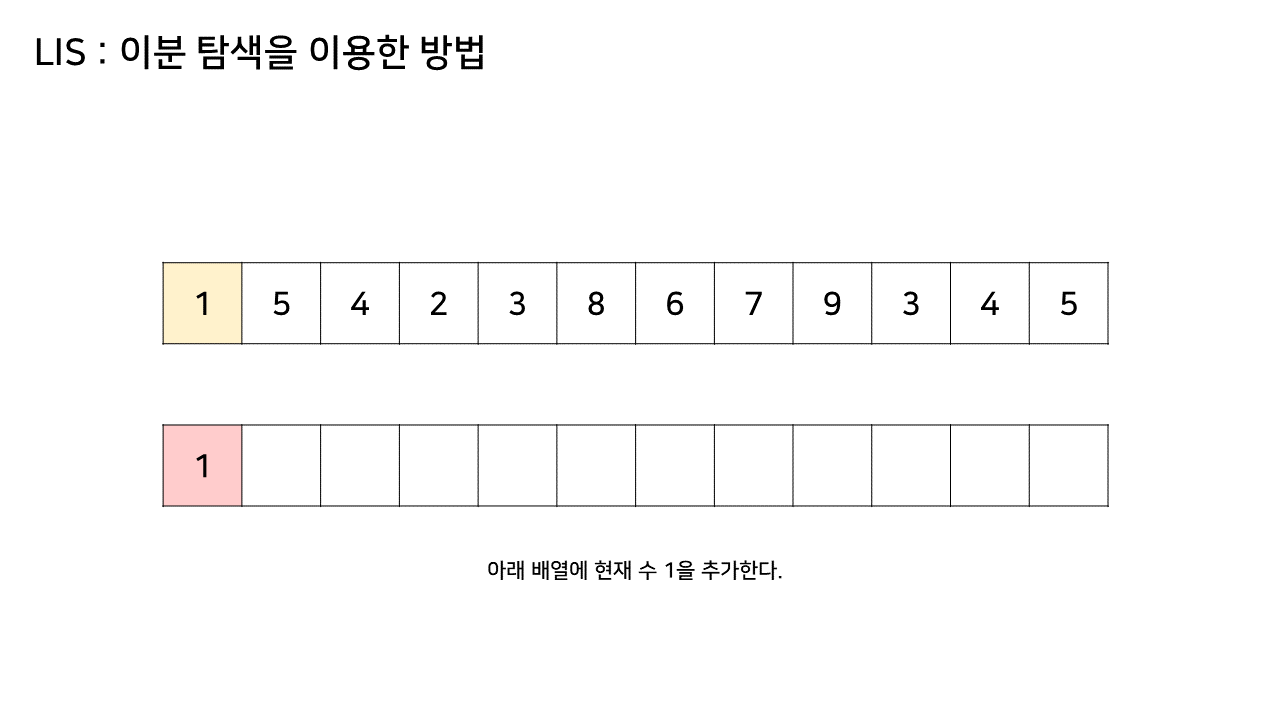
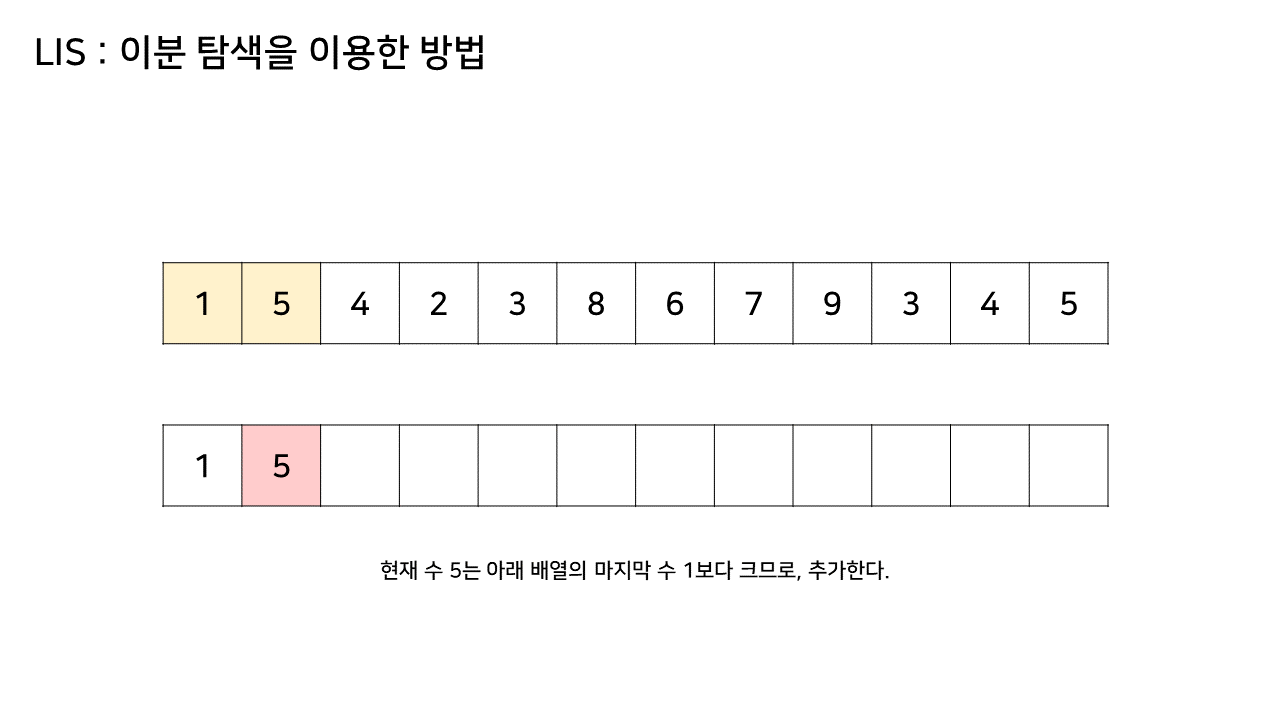
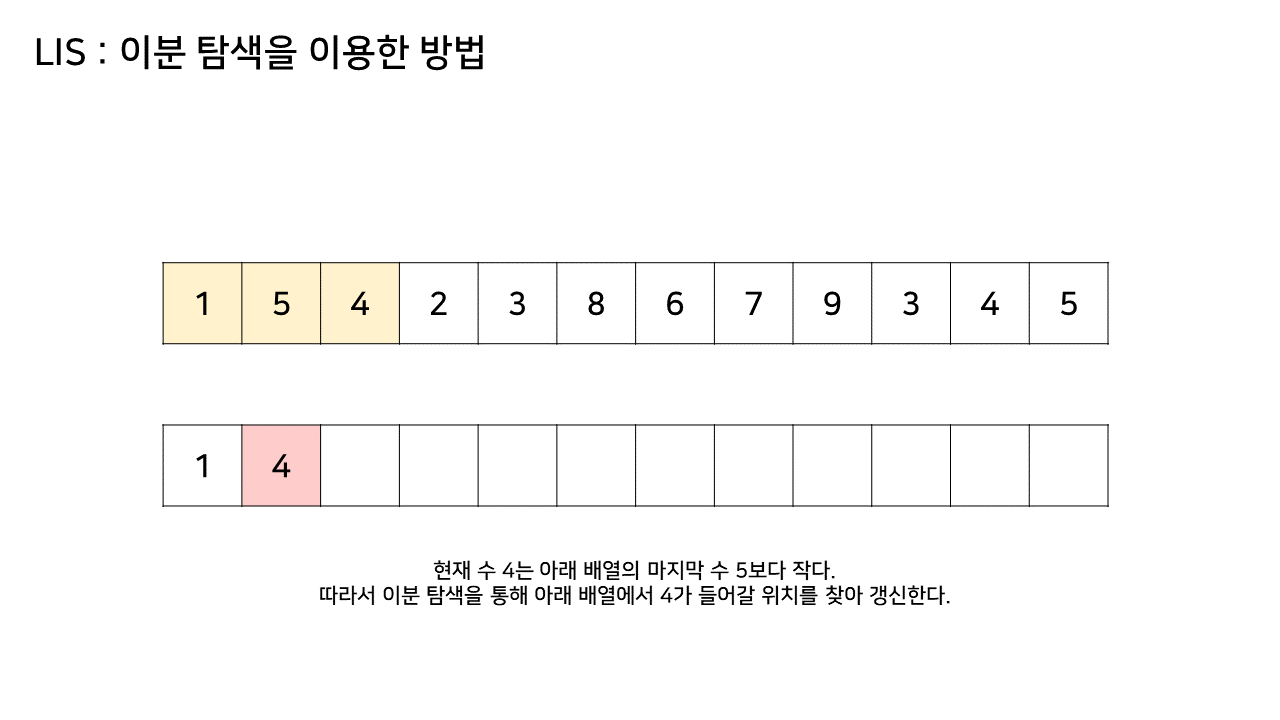
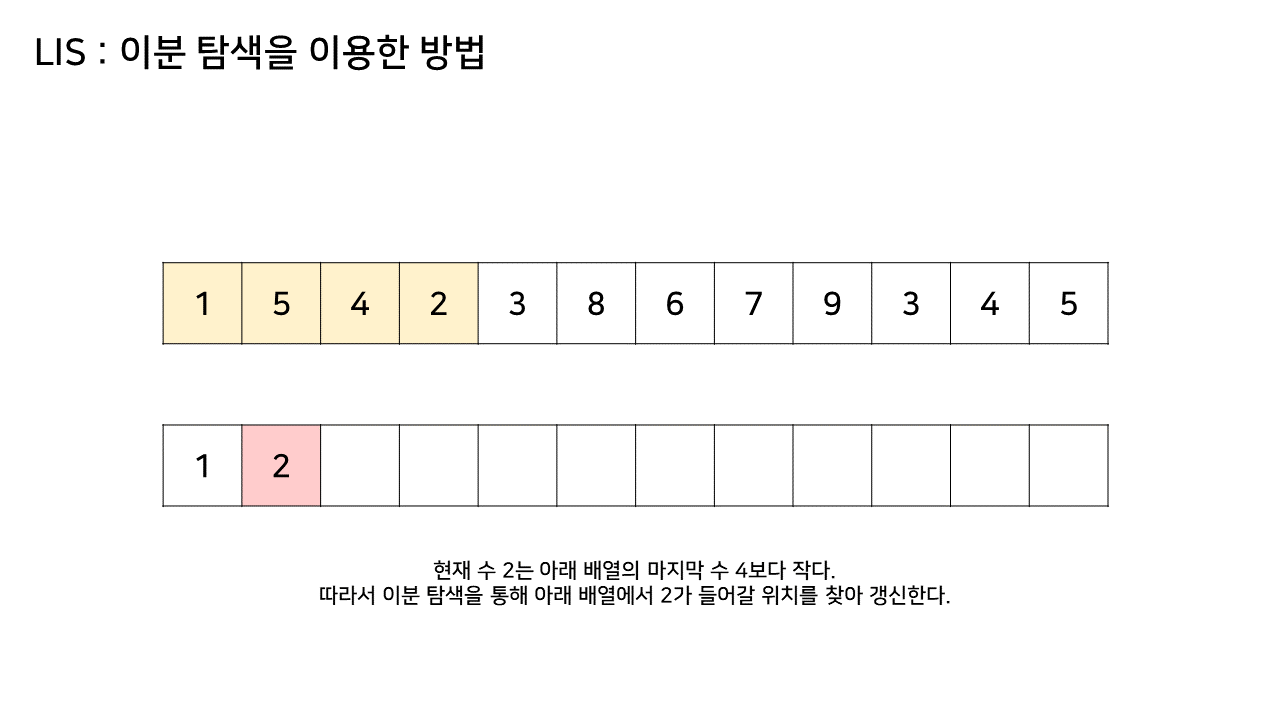
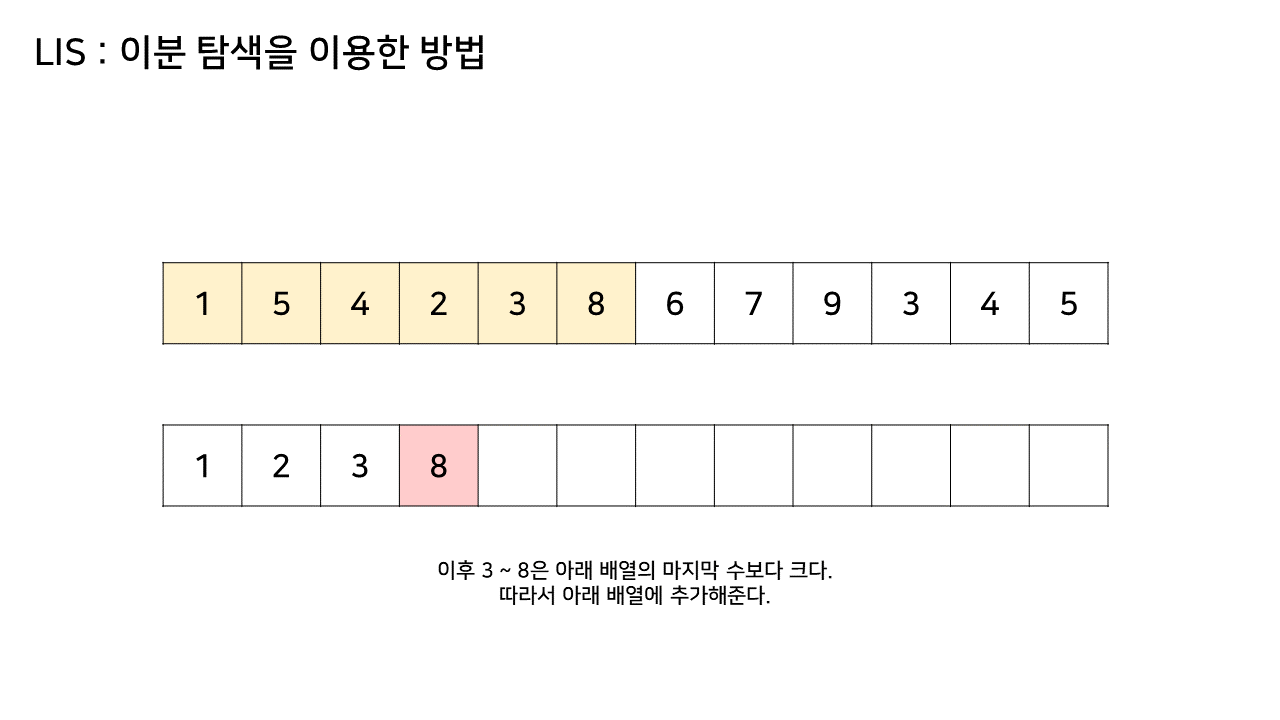
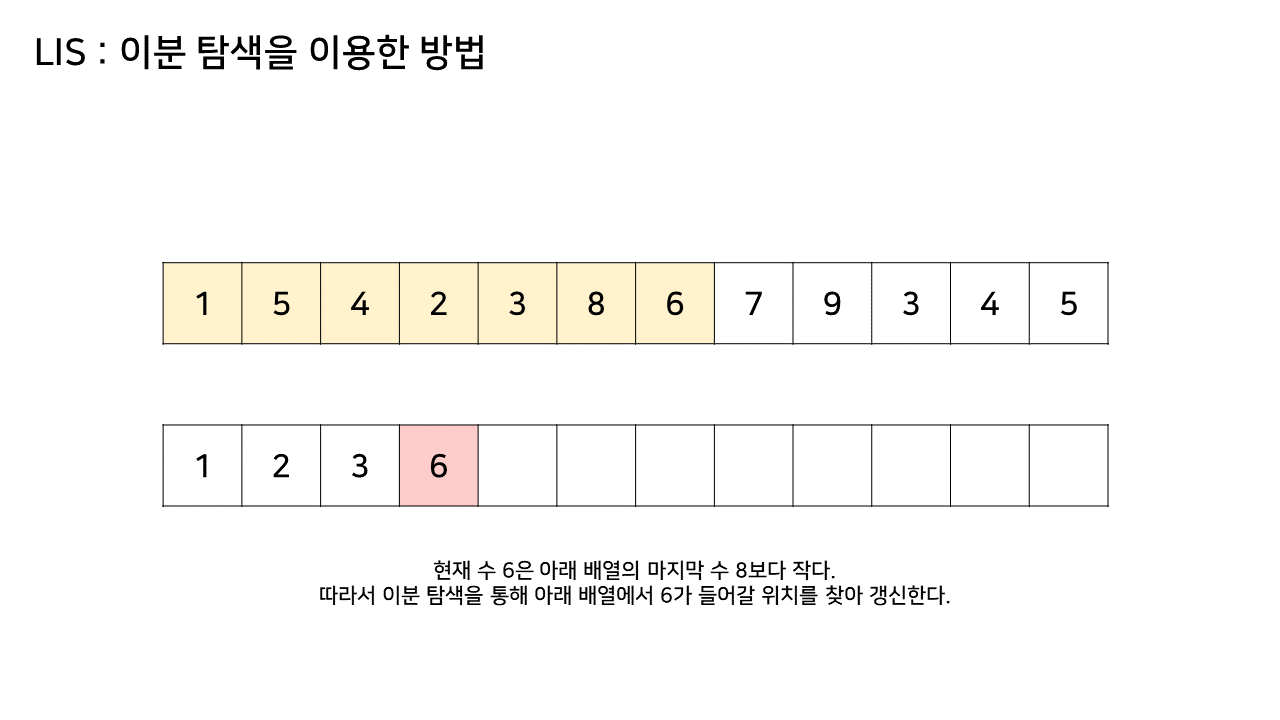
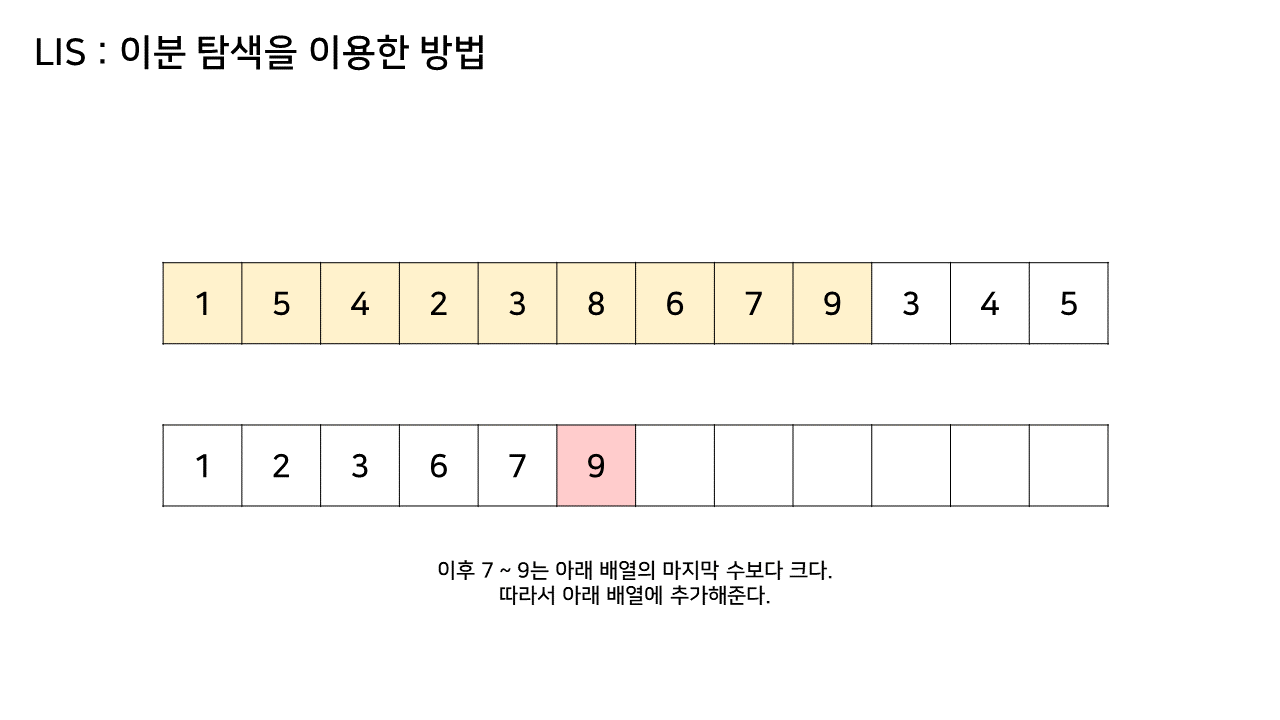
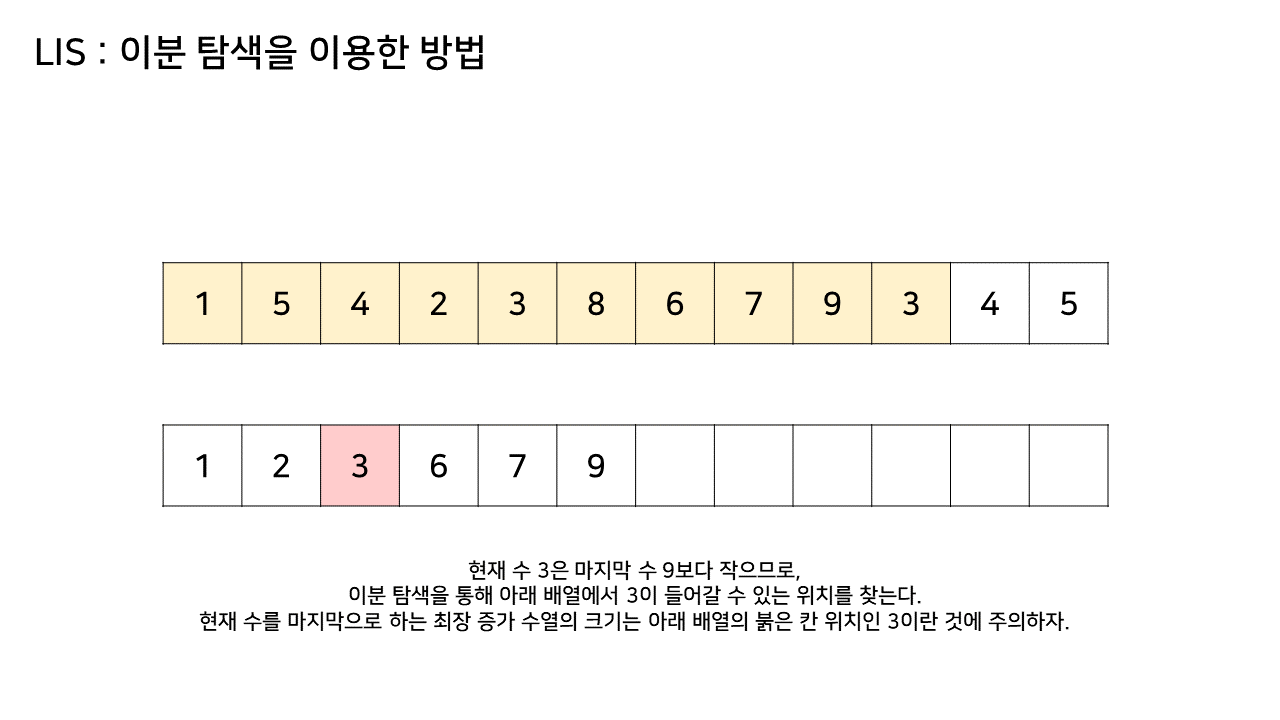
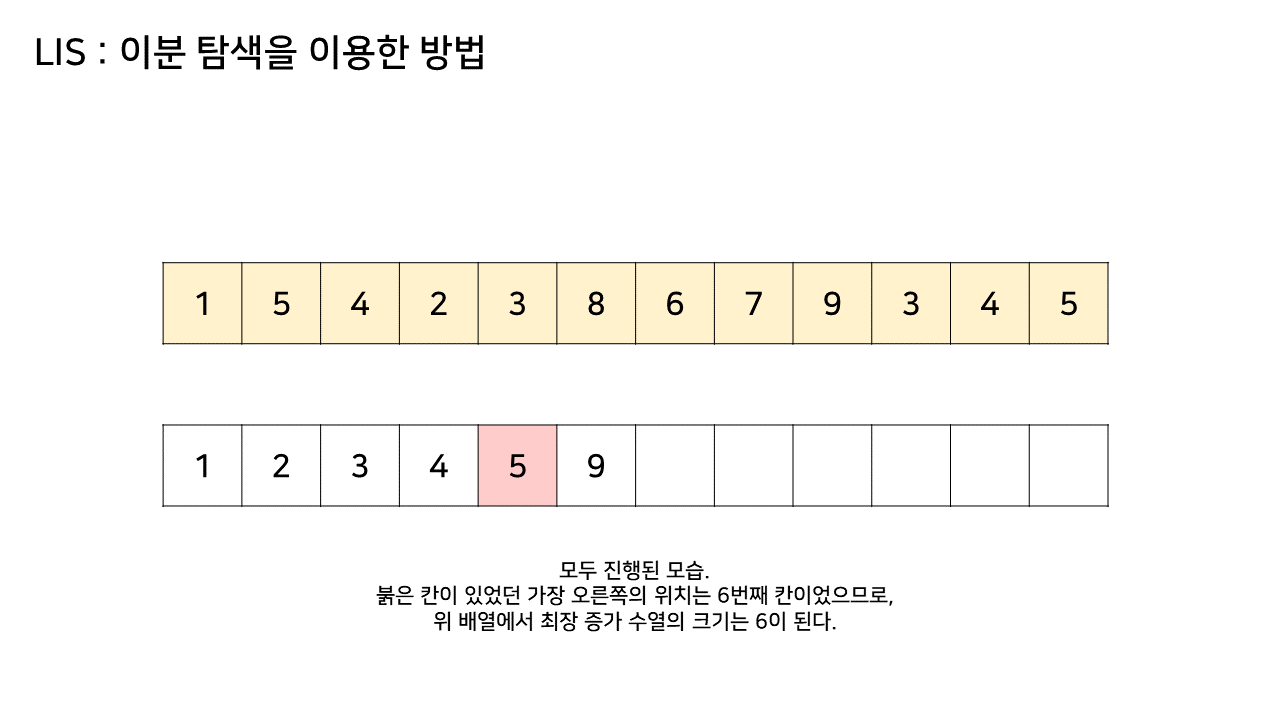
• 그림에서 LIS 수열을 저장하는 하나 추가된 배열에서 최대 크기가 6이었으므로, LIS의 길이는 6이된다
• 이 방법은 그림의 아래 배열을 LIS 형태로 유지하기 위해, 기존 수열의 각 원소가 LIS에 들어갈 위치를 찾는 원리로 동작한다
• 즉, 현재 원소를 아래 배열에 넣어 LIS를 유지하려고 할 때, 그 최적의 위치를 찾는 것이다
• 코드

int binary_search(vector<int> lis, int start, int end, int element) {
    //이분 탐색으로 lis 벡터 내에서 element의 위치를 반환
    //lis 벡터의 start - end 구간에서만 확인
    while (start < end) {
        int mid = (start + end) / 2;
        if (element > lis[mid]) start = mid + 1;
        else end = mid;
    }
    return end;
}
 
int LIS_BS() {
    int ret = 0;
    vector<int> lis;
    lis.push_back(arr[0]);
 
    for (int i = 1; i < n; i++) {
        //만약 lis 벡터의 마지막 수보다 i번째 수가 크다면, 그냥 뒤에 붙인다.
        if (arr[i] > lis.back()) {
            lis.push_back(arr[i]);
            ret = lis.size() - 1;
        }
        //i번째 수에 대해, lis 벡터 내에서 그 수의 위치를 찾는다.
        int pos = binary_search(lis, 0, ret, arr[i]);
        lis[pos] = arr[i];
    }
 
    return ret + 1;
}

그림 출처: https://4legs-study.tistory.com/106