[Algorithm] 99클럽 코테 스터디 2일차 TIL BOJ 1654

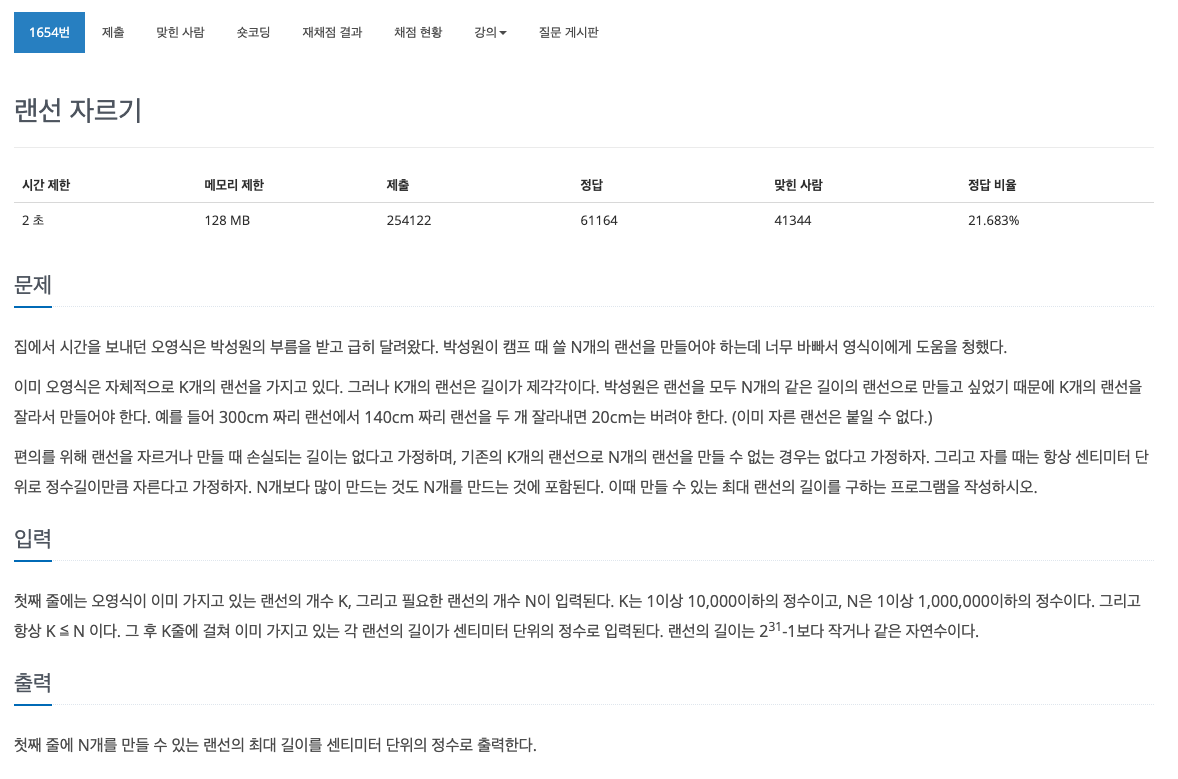
문제

https://www.acmicpc.net/problem/1654

풀이

문제 분석

• 주어진 개수를 만들 수 있는 랜선의 최대 길이를 구해야 한다
• 이때, 구한 길이로 만들 수 있는 랜선의 개수는 주어진 개수와 같거나 그 개수보다 클 수 있다
• 이분탐색을 이용하여 랜선의 길이를 구할 수 있다
• 이때, 이분 탐색의 일반적인 풀이법(인덱스를 구하는 방법)을 조금 변경하여 생각해 랜선의 길이를 구하도록 한다

코드

import java.io.*;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        String[] token = br.readLine().split(" ");
        long K = Long.parseLong(token[0]);
        int N = Integer.parseInt(token[1]);
        long[] youngsik = new long[(int) K];
        long max = 0;
        long count = 0;
        for(int i=0 ; i<K ; i++) {
            youngsik[i] = Integer.parseInt(br.readLine());
            if(max < youngsik[i]) {
                max = youngsik[i];
            }
        }

        max++; // upper bound

        long min = 0;
        long mid;

        while(min < max) {

            mid = (min + max) / 2;

            count = 0;

            for (int i = 0; i < K; i++) {
                count += (youngsik[i] / mid);
            }

            if(count < N) {
                max = mid;
            }
            else {
                min = mid + 1;
            }
        }
        bw.write(String.valueOf(min-1));
        bw.flush();
        bw.close();
    }
}

TIL

오늘의 문제는 이분 탐색이라는 힌트를 보고도 해결하지 못했다.
일단 이분 탐색 힌트를 본 이후에 길이를 이분 탐색으로 구하려고 하였으나 upper bound를 생각하지 못해 해결하지 못했다.

그래서 이분 탐색 알고리즘과 upper bound, lower bound를 정리해보려고 한다.

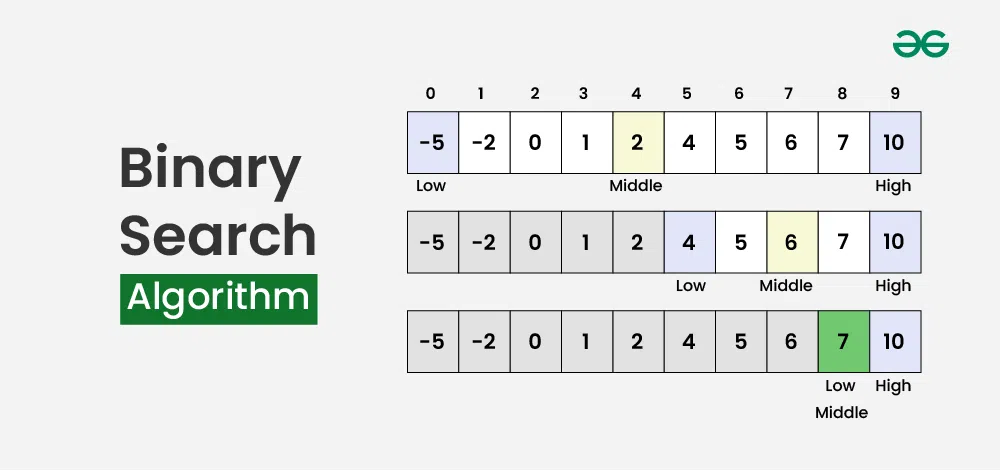
이분 탐색 알고리즘

• 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법이다
• 배열 내부의 데이터가 정렬되어 있어야만 사용할 수 있는 알고리즘이다
• 변수 3개(start(min), end(max), mid)를 사용하여 탐색한다
• 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는다
  

• 이진 탐색 알고리즘 자바 코드

public class BinarySearch {

	public static void main(String[] args) {
        int[] array = {2, 3, 4, 10, 40};
        int target = 10;
        int result = binarySearch(array, target);
        if (result == -1) {
            System.out.println("Element not present");
        } else {
            System.out.println("Element found at index " + result);
        }
    }
    
    public static int binarySearch(int[] array, int target) {
        int left = 0;
        int right = array.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2; // 중간 인덱스 계산

            // 타겟을 찾았을 때
            if (array[mid] == target) {
                return mid;
            }

            // 타겟이 중간 값보다 작을 경우
            if (array[mid] > target) {
                right = mid - 1;
            } 
            // 타겟이 중간 값보다 클 경우
            else {
                left = mid + 1;
            }
        }

        // 타겟을 찾지 못했을 때
        return -1;
    }
}

upper bound vs lower bound

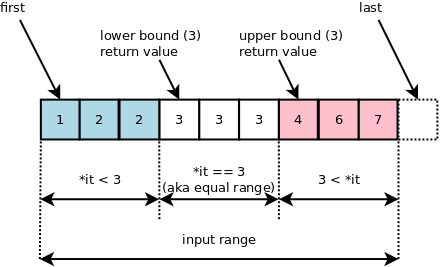
• upper bound(상한): 찾고자 하는 특정 값을 초과하는 '첫 위치'를 반환한다
• lower bound(하한): 찾고자 하는 특정 값 이상인 '첫 위치'를 반환한다
• 이진 탐색이 데이터 내 특정 값을 정확히 찾는 방법이라면, lower bound와 upper bound는 이진 탐색 알고리즘에서 약간 변형된 것으로 중복된 자료가 있을 때 유용하게 탐색할 수 있는 알고리즘이다

• 위 그림을 참고하면 중복된 값(2 or 3)이 존재한다

• 배열을 정렬한 상태에서 3의 값을 기준으로 lower_bound(3)을 호출하면 3과 같으면서 3보다 큰 값이 최초로 나타나는 index = 3을 리턴한다

• upper_bound(3)을 호출하면 3보다 큰 값이 제일 처음으로 나오는 index = 6을 호출한다

• 이에 따라 이번 백준 1654에서는 개수가 중복이 될 때 최대 길이를 찾아야 하므로 upper bound를 이용하여 얻어진 값에서 -1을 해주면 최대 길이가 되는 것이었다

• 또한 자바에서는 upper_bound, lower_bound를 라이브러리를 통해 제공하지 않으므로 다음과 같이 구현할 수 있다고 한다

• upper_bound

private static int upperBound(List<Integer> data, int target) {
    int begin = 0;
    int end = data.size();
    
    while(begin < end) {
    	int mid = (begin + end) / 2;
        
        if(data.get(mid) <= target) {
        	begin = mid + 1;
        }
        else {
        	end = mid;
        }
    }
    return end;
}

• lower bound

private static int lowerBound(List<Integer> data, int target) {
    int begin = 0;
    int end = data.size();
    
    while(begin < end) {
    	int mid = (begin + end) / 2;
        
        if(data.get(mid) >= target) {
        	end = mid;
        }
        else {
        	begin = mid + 1;
        }
    }
    return end;
}