[Algorithm] 99클럽 코테 스터디 9일차 TIL BOJ 1707

문제

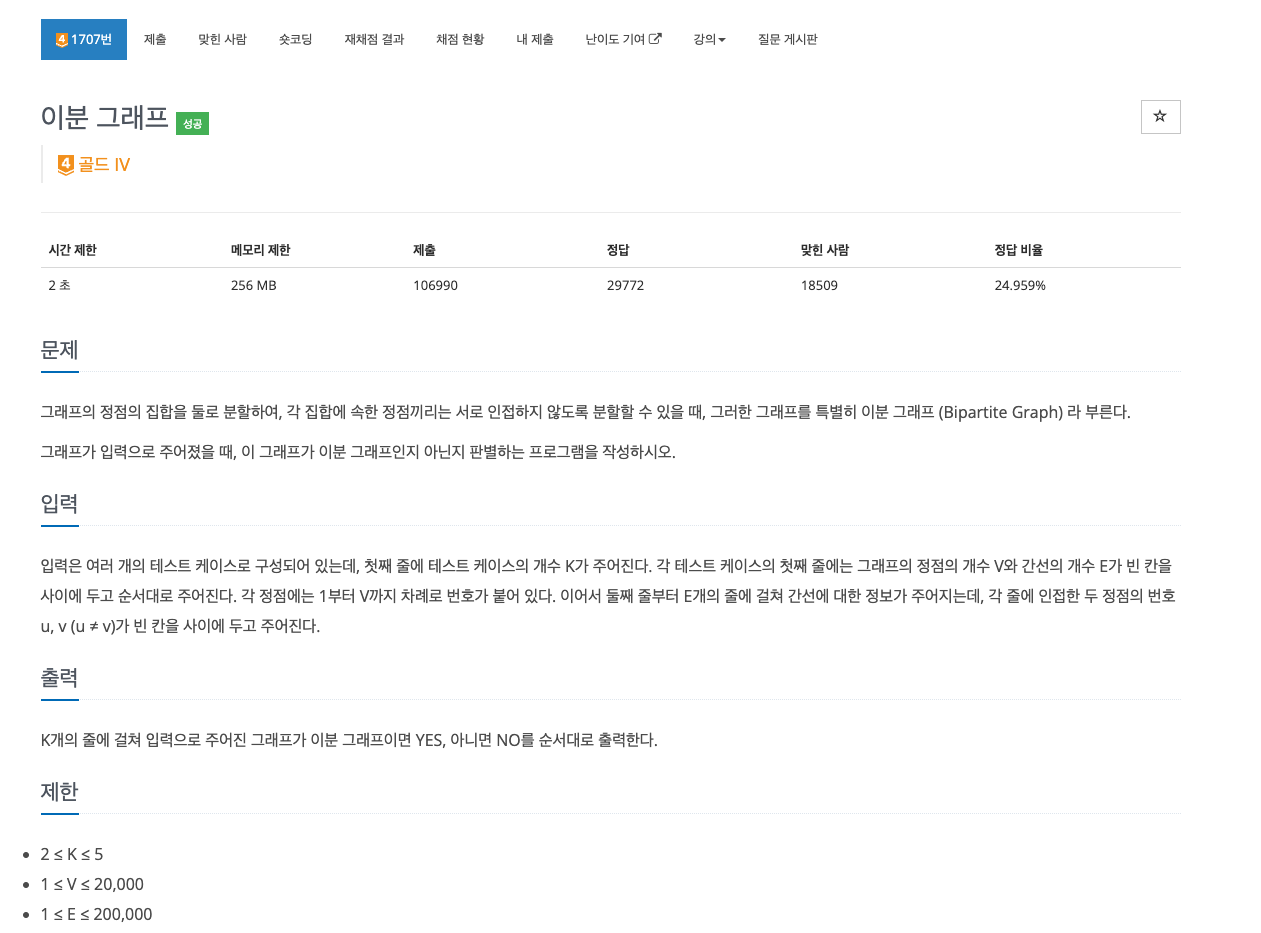
https://www.acmicpc.net/problem/1707

풀이

문제 분석

• 이분 그래프에서는 색상 감지가 중요하다는 것을 생각해내지 못했고, 이로 인해 답을 맞추지 못했었다
• 초기에 작성했던 코드는 사이클 감지를 통해 이분 그래프인지를 확인했었고 항해 99에서 제공하는 문제 풀이 시간이 끝나 답을 확인하는 과정에서 색상 배열을 사용해야 한다는 것을 알게 되었다
• 수정한 코드는 다음과 같다

코드

import java.io.*;
import java.util.*;

public class Main {
    private static int TC = 0;
    private static int[] colors;
    private static List<Integer>[] graph;
    private static boolean isBinaryGraph;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        TC = Integer.parseInt(br.readLine());

        for(int i = 0 ; i < TC; i++) {
            isBinaryGraph = true;
            String[] token = br.readLine().split(" ");
            int V = Integer.parseInt(token[0]);
            int E = Integer.parseInt(token[1]);
            colors = new int[V+1];
            graph = new ArrayList[V+1];
            for (int j = 1; j <= V; j++) {
                graph[j] = new ArrayList<>();
            }

            for(int j = 0 ; j < E ; j++) {
                token = br.readLine().split(" ");
                int x = Integer.parseInt(token[0]);
                int y = Integer.parseInt(token[1]);
                graph[x].add(y);
                graph[y].add(x);
            }

            for (int j = 1; j <= V; j++) {
                if (colors[j] == 0) {
                    dfs(j, 1);
                }
            }

            if(isBinaryGraph)
                System.out.println("YES");
            else
                System.out.println("NO");
        }
    }

    private static void dfs(int node, int color) {
        colors[node] = color;

        for (int neighbor : graph[node]) {
            if (colors[neighbor] == 0) {
                dfs(neighbor, 3 - color);
            } else if (colors[neighbor] == color) {
                isBinaryGraph = false;
            }
        }
    }
}

TIL

• 이분 그래프 (Bipartite Graph): 그래프 이론에서 두 개의 독립적인 집합으로 정점을 나눌 수 있는 그래프
• 이렇게 나눈 두 집합의 정점들 사이에만 간선이 존재하며, 같은 집합 내의 정점들 사이에는 간선이 없음
• 특징

1. 두 집합으로 분할 가능하며, 내부 정점들 사이에는 간선이 없음
2. 사이클의 길이: 이분 그래프는 홀 수 길이의 사이클을 포함하지 않음
3. 색칠: 이분 그래프의 정점들은 두 가지 색으로 색칠할 수 있음 -> 인접한 정점은 서로 다른 색으로 색칠되어야 함