AVL Tree
• 모든 노드에 대해 좌서브 트리의 높이 (hL; height of Left subtree)와 우서브 트리의 높이 (hR; height of Right subtree) 의 차가 1을 넘지 않는다
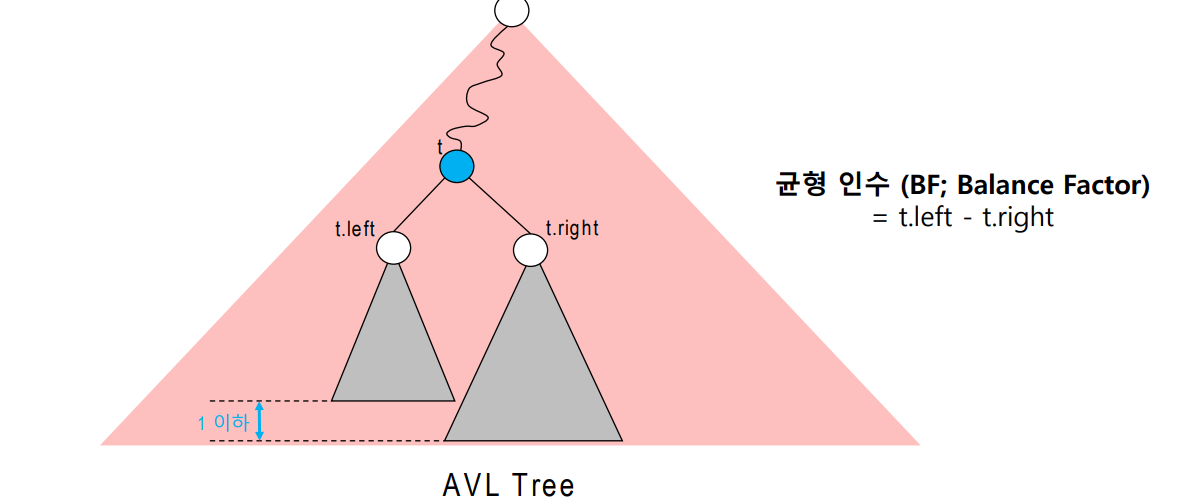
• 모든 노드에 대해 좌서브 트리의 높이(깊이)와 우서브 트리의 높이의
차가 1을 넘지 않는다
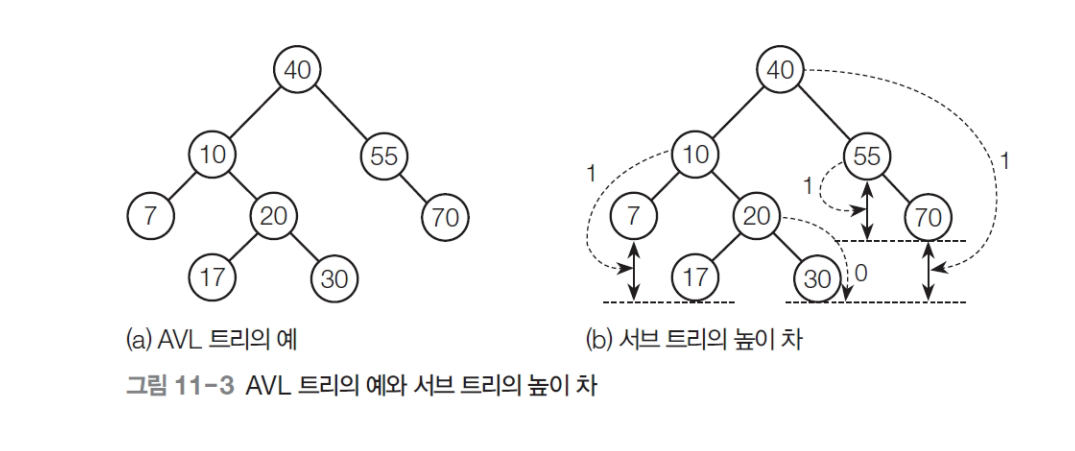
b는 균형이 잘 맞아있다.
- 2이상은 AVL트리가 아니다.

노드(트리)의 회전
회전으로 균형을 맞춘다.(균형이 깨졌을 때)
-
회전축이 8/5 위치임 (위에 숫자는 균형인수이다.)
6의 위치가 변함
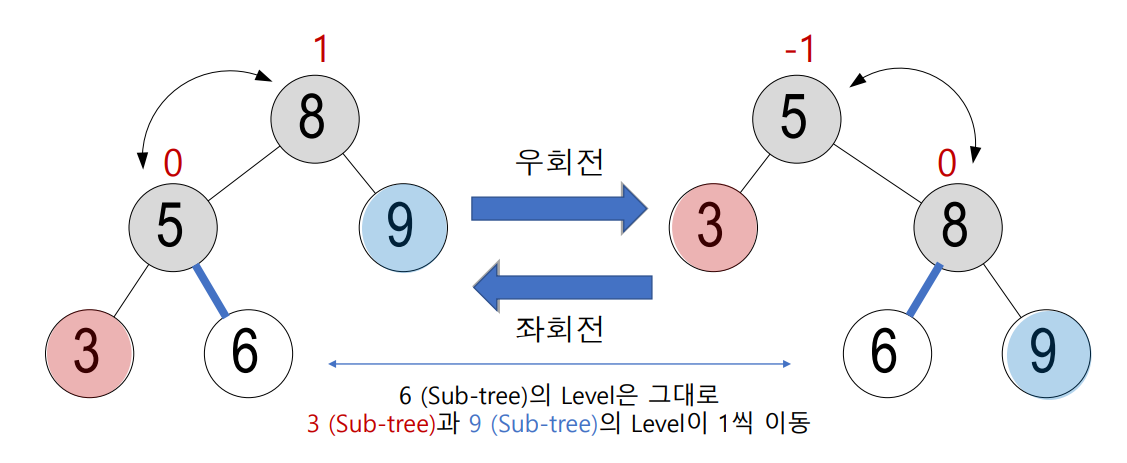
-
좌회전으로 균형을 맞추는 예시
AVL 트리로 수선

-
좌회전으로 두 곳의 불균형을 해결하는 예
17의 높이는 변하지 않음(자식의 높이는 변하지 않고 부모가 바뀜)
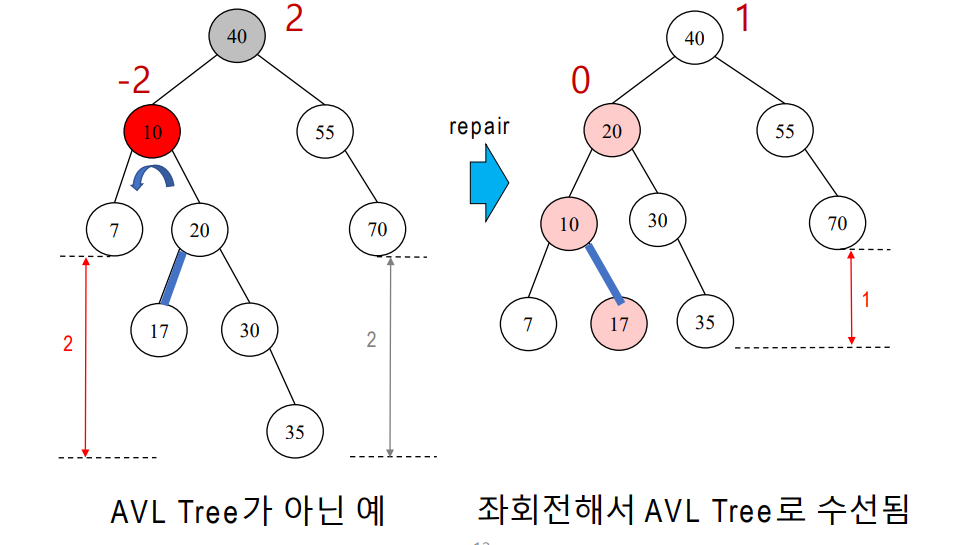
-
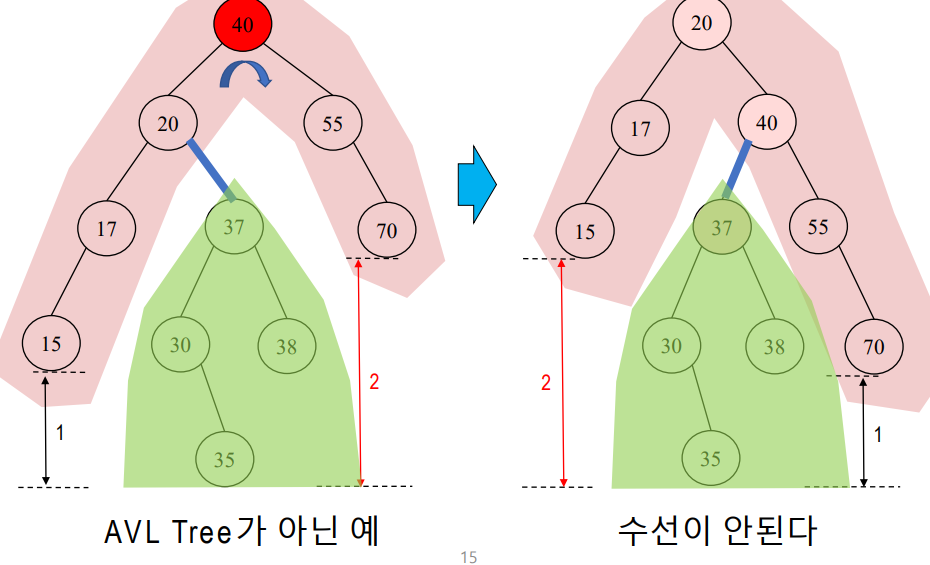
단순한 회전으로 해결이 안 되는 예 (우회전)
35와 15와의 차이로 해결이 안되므로 우회전으로는 해결할 수 없다.

빨간색 부분과 녹색 부분의 차이로 발생함
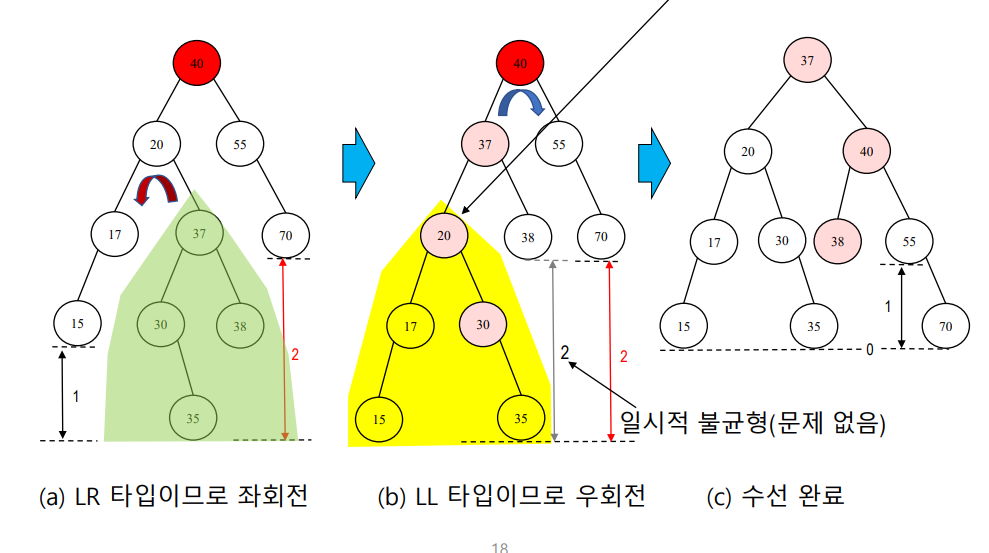
→ 좌회전 해서(먼저 종속성이 없어짐) 서브 트리의 왼쪽이 더 높게 만든 다음 우회전
바깥쪽 부분을 길게 만들어야 함.
작은 애들부터 돌리고 큰 부분을 돌린다.
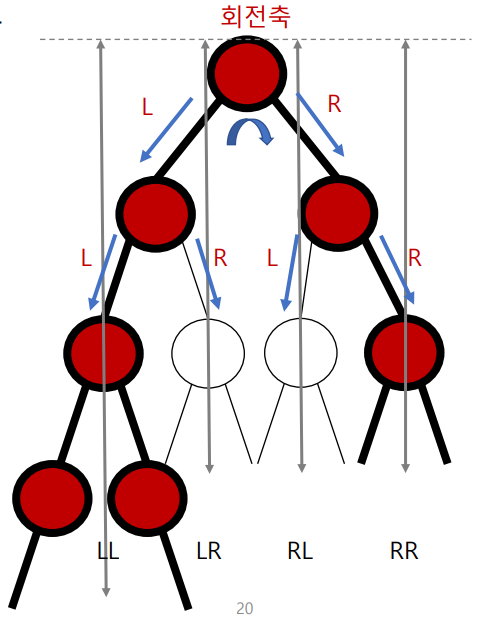
AVL Tree의 회전(4가지)
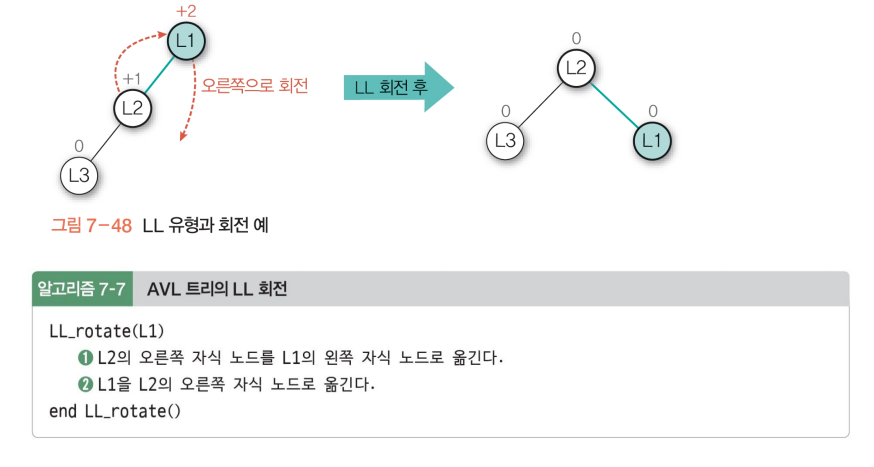
• Case 1: LL이 가장 깊음
→ 단일 우회전, LL회전
왼쪽이 가장 깊을 때는 LL(왼쪽이 가장 길어서)회전(우회전)
• Case 2: RR이 가장 깊음
→ 단일 좌회전, RR회전
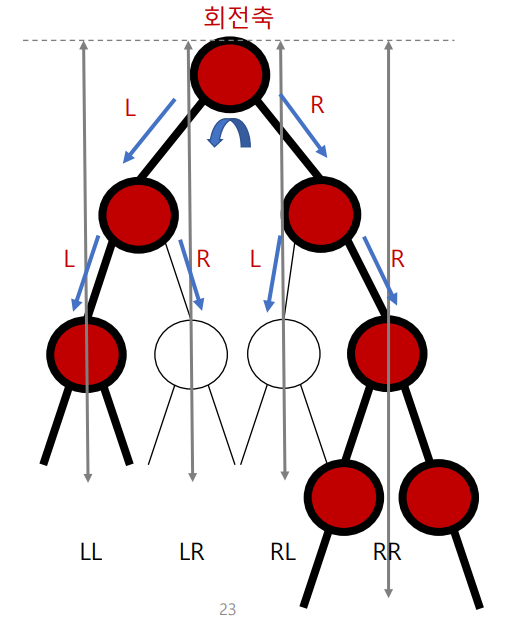
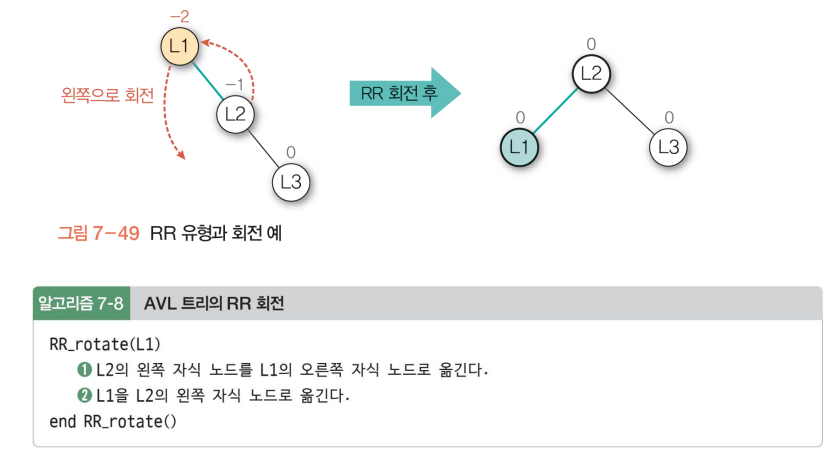
• Case 3: LR이 가장 깊음(왼쪽 자식의 오른쪽이 가장 깊을 경우)
→ 이중 회전, 자식 RR 회전 후 LL 회전
회전축의 왼쪽 자식을 축으로 해서 좌회전을 하고 원래 회전축에 대해 우회전을 하면 된다.

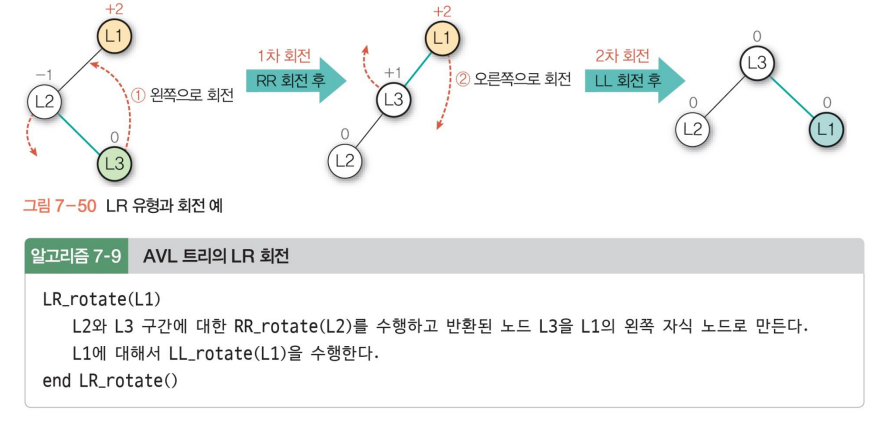
• Case 4: RL이 가장 깊음(오른쪽 자식의 왼쪽이 가장 깊을 경우)
→ 이중 회전, 자식 LL회전 후 RR회전
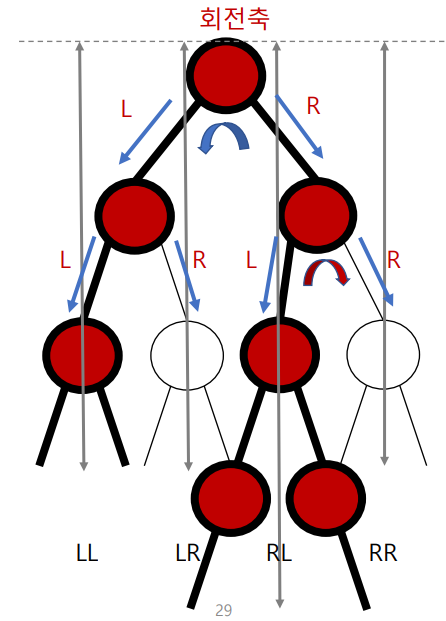

루트를 타고 올라가면서 균형인수가 맞을 때까지 수선하면 AVL 트리가 된다.

코드 정리
balanceAVL(t, type):
if (type == LR):
RR(t.right)
elif (type == RL):
LL(t.left)
if (type == LR or type == LL):
LL(t)
else:
RR(t)
