[Java] ArrayList vs LinkedList

Eunbi Lee·2023년 4월 26일

Java

목록 보기

4/5

[자바의 신]을 읽으면서 ArrayList와 LinkedList의 개념 및 시간 복잡도에 관련해서 정리 글을 작성하게 되었습니다.

깃허브에 정리하는 것만으로는 부족하다고 생각이 들었네요. 💬

Collection이란?

[자바의 신] 자바에서 목록성 데이터를 처리하는 자료 구조

Collection(컬렉션)이란 데이터를 저장하는 자료 구조와 데이터를 처리하는 알고리즘을 구조화하여 클래스로 구현한 것이다.

기존에는 여러 개의 객체들을 하나의 객체에 담기 위해서 Object 클래스의 배열을 사용했지만, 배열의 경우 정적 메모리 할당(선언한 크기의 공간만큼 사용)을 하는 반면 컬렉션은 동적 메모리 할당(공간이 계속 필요한만큼 추가)을 하기 때문에 메모리 면에서 효율적으로 사용할 수 있다.

자바의 컬렉션의 구조는 다음과 같다.

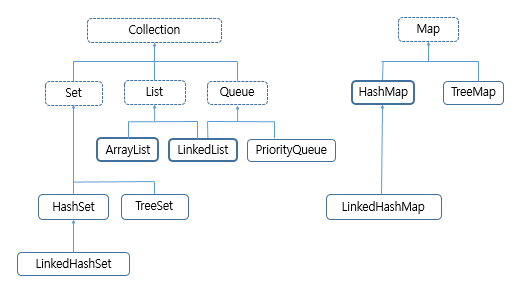
Collection(인터페이스)

List, Set, Queue (인터페이스)
- ArrayList, LinkedList, .. (클래스)

별개로 Map은 컬렉션에 속하지만 따로 분류된다.

Map (인터페이스)
- HashMap, .. (클래스)

📚 ArrayList란?

ArrayList란 자바의 컬렉션 중 하나로서, 동적 배열을 구현한 클래스

이때, 동적 배열이란 할당된 ArrayList의 배열 공간이 꽉 찼을 때 새로운 배열을 만들어서 기존의 내용을 자동으로 복사하는 과정을 일컫는다.

일반적으로 기존 배열의 크기는 10이며, 새로운 배열을 생성할 시 1.5배 확장

지금까지 설명한 ArrayList를 그림으로 표현하면 다음과 같다.

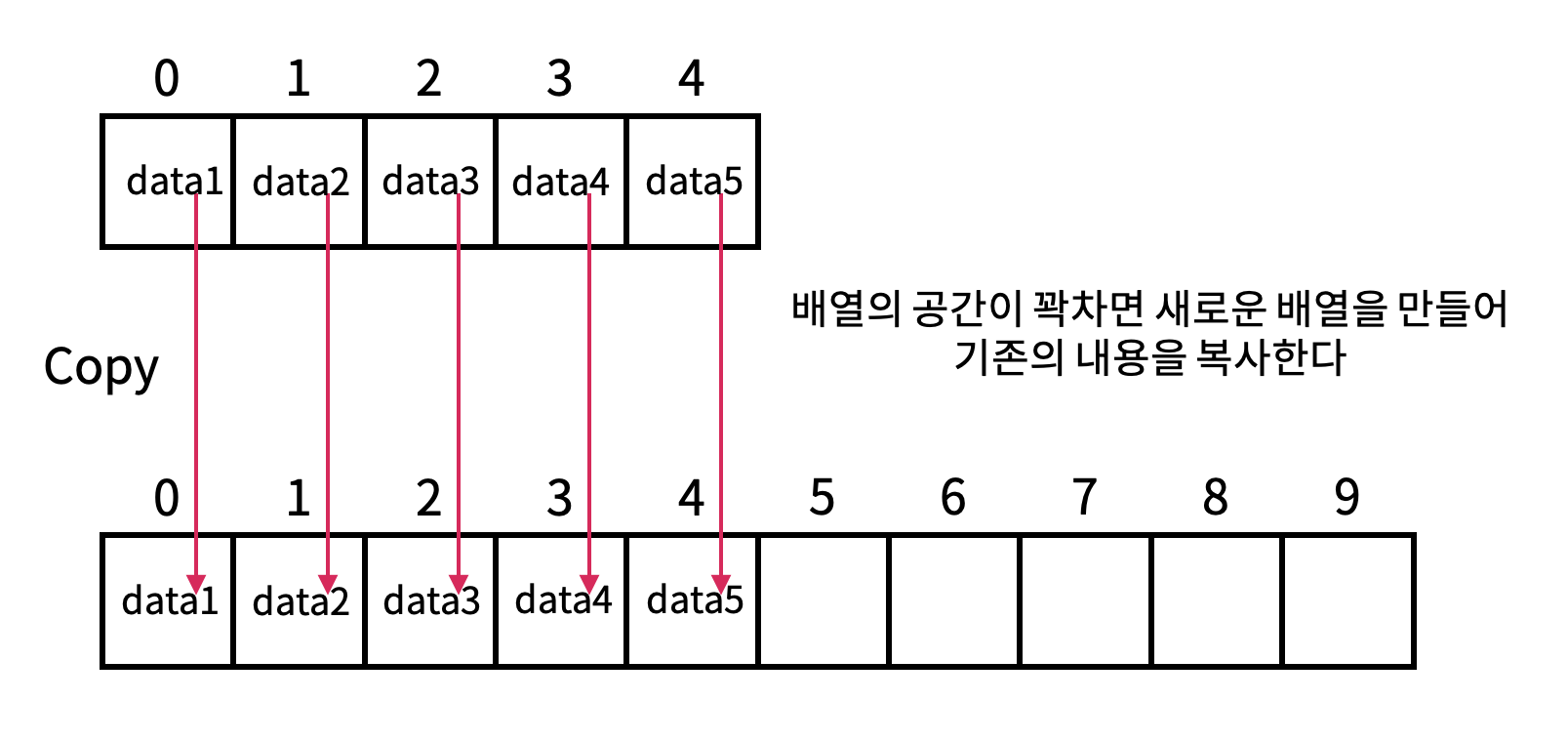
출처 : https://www.codelatte.io/courses/java_programming_basic/5N27027VT1DBUAX0

ArrayList의 특징

내부적으로 Object 타입의 배열([ ]) 구조로 구성되어 있으며 인덱스를 기반으로 각각의 요소(element)에 접근하여 검색(get()), 추가(add()), 삭제(remove()) 등의 작업을 수행할 수 있다.
중복된 데이터를 허용하며 입력된 순서대로 요소가 저장된다.
인덱스를 통해 각각의 요소에 접근할 수 있기 때문에 검색에 용이하다.

Obejct 클래스 타입의 배열 vs ArrayList

위에서 살펴본 내용에 의하면 Object 클래스 타입의 배열, 즉 기존 배열([ ])과 ArrayList는 내부적으로 동일한 배열 구조를 가지고 있다.

그렇다면 왜 ArrayList를 사용하는걸까?

답은 여러 이유가 있지만, 대표적인 이유는 위에서 잠깐 등장했던 동적 배열 개념 때문이다.

먼저 배열은 생성할 때, 고정된 크기를 선언하기 때문에 현재 배열이 꽉 찼을 경우 재생성한 뒤 기존 요소를 복사해야 한다.

반면 ArrayList는 더 큰 크기의 배열이 필요한 경우, 자동으로 배열의 크기를 늘릴 수 있다.

그리고 배열으로 연산을 수행할 경우 일반 산술 연산자를 사용하여 수행하는 반면, ArrayList의 경우 다양한 메소드를 통해 수행할 수 있다.

add(), remove(), get() 등

또한, 배열은 Object 타입이기 때문에 모든 객체 타입을 저장할 수 있지만 동시에 형 변환(type casting)이 필요할 수도 있다.

하지만, ArrayList의 경우 제네릭(Generic)을 지원하기 때문에 제네릭을 사용한 ArrayList를 생성하면 특정 타입의 객체만 저장할 수 있기 때문에 타입 안정성이 높아진다. 즉, 형 변환이 필요하지 않다.

ArrayList의 시간 복잡도

주요 메소드들에 따라 시간 복잡도의 차이가 있다.

1. get(int index)

인덱스에 해당하는 요소를 리턴한다.

시간 복잡도 : O(1)

ArraList는 내부적으로 배열을 사용하기 때문에, 인덱스를 통해 요소에 직접 접근할 수 있다. 따라서 get() 메소드의 시간 복잡도는 상수 시간이다.

2. add(E element)

주어진 요소를 ArrayList의 끝에 추가한다.

시간 복잡도 : 평균적으로 O(1)

ArrayList의 늘리는 작업이 필요하지 않는 한, 요소를 추가하는데 걸리는 시간 복잡도는 상수 시간이다.

3. add(int index, E element)

주어진 인덱스에 요소를 삽입한다. 이때, 해당 인덱스부터 뒤에 있는 요소들은 한 칸씩 뒤로 밀린다.

시간 복잡도 : O(n) (n은 ArrayList의 요소 개수)

자세하게 세 가지 경우로 나뉠 수 있다.

맨 앞에 추가하는 경우 (index = 0)
모든 요소를 한 칸씩 뒤로 이동시켜야 하므로 시간 복잡도는 최악의 경우 O(n)이다.
중간에 추가하는 경우 (0 < index < n)
해당 인덱스부터 끝까지의 요소를 한 칸씩 뒤로 이동시켜야 하므로 시간 복잡도는 O(n/2)(=O(n))이지만, 최악의 경우는 O(n)이다.
맨 뒤에 추가하는 경우 (index = n)
요소를 이동시키지 않아도 되므로 시간 복잡도는 O(1)이다.

4. remove(int index)

주어진 인덱스에 해당하는 요소를 제거하고, 그 위치 이후의 요소들을 한 칸씩 앞으로 이동시킨다.

시간 복잡도 : O(n)

5. remove(Object o)

주어진 객체와 일치하는 첫 번째 데이터를 제거하고, 그 위치 이후의 데이터들을 한 칸씩 앞으로 이동시킨다.

시간 복잡도 : O(n) (n은 ArrayList의 요소 개수)

첫 번째로 일치하는 데이터를 찾기 위해 리스트를 맨 앞부터 순회한다. 따라서 remove(Object o)의 시간 복잡도는 O(n)이다.

🚃 LinkedList란?

LinkedList란 자바의 컬렉션 중 하나로서, 노드와 포인터로 이루어져 있는 클래스

LinkedList는 데이터를 배열에 저장하는 구조가 아니라, 노드(Node)에 데이터(value)와 이전 노드를 가리키는 포인터(prev), 다음 노드를 가리키는 포인터(next)를 가지고 있다.

노드(Node) : 데이터를 담고있는 값(value)을 저장
이전 포인터(prev) : 노드가 이전 노드를 가리키는 포인터이며, 이 포인터를 통해 이전에 위치한 노드와 연결되며 탐색할 수 있음
- 첫 번째 노드인 경우, 이전 포인터는 null 값
다음 포인터(next) : 노드가 다음 노드를 가리키는 포인터이며, 이 포인터를 통해 다음에 위치한 노드와 연결되며 탐색할 수 있음
- 마지막 노드인 경우, 다음 포인터는 null 값

즉, LinkedList는 포인터를 통해 양방향 탐색(처음 또는 마지막 위치에서부터 한 방향으로 탐색)이 가능하다.

지금까지 설명한 LinkedList를 그림으로 표현하면 다음과 같다.

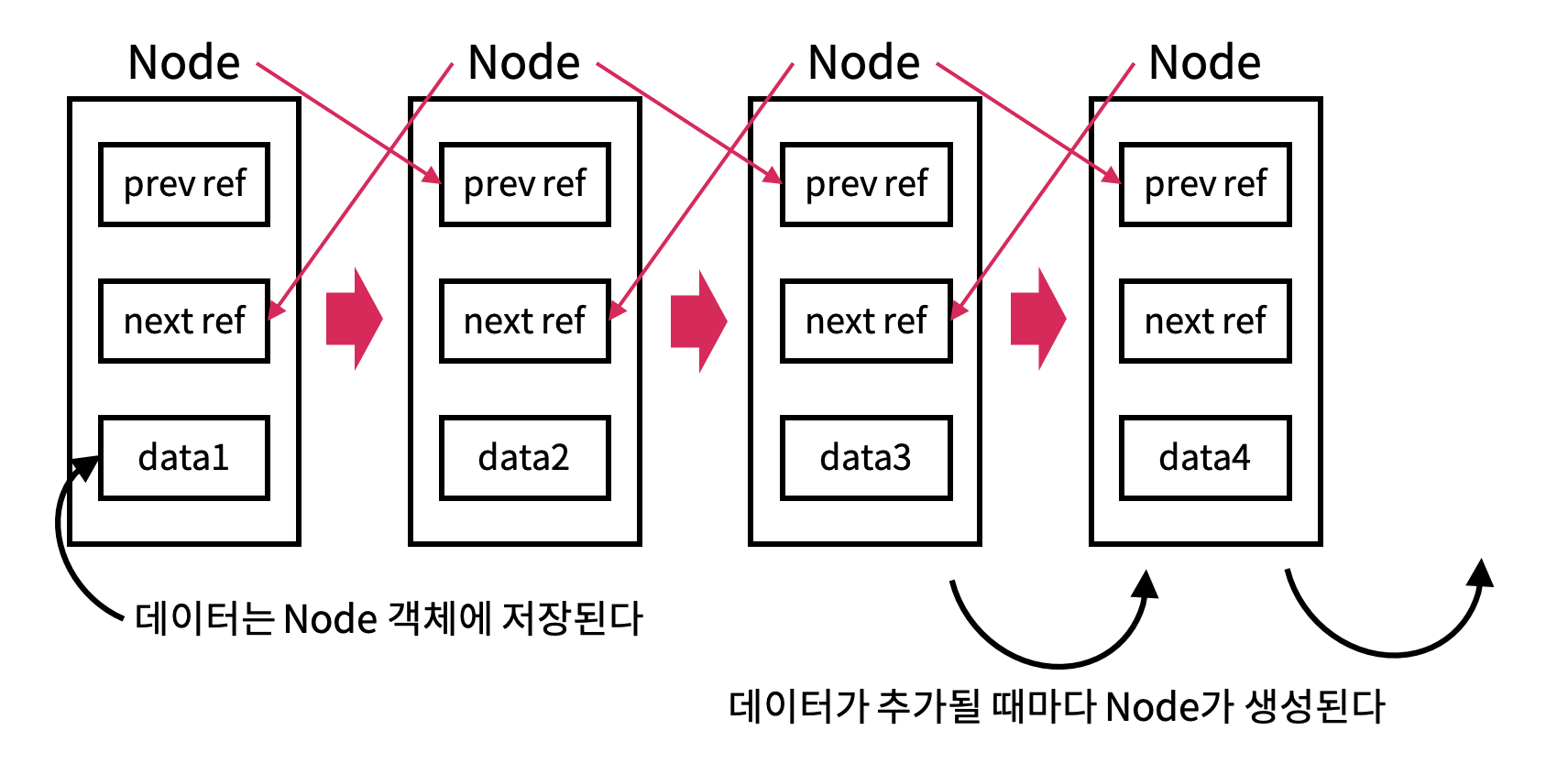
출처 : https://www.codelatte.io/courses/java_programming_basic/5N27027VT1DBUAX0

LinkedList의 특징

내부적으로 노드와 포인터(=링크)를 가진 구조로 구성되어 있으며, 포인터를 통해 각각의 노드에 접근하여 검색(get()), 추가(add()), 삭제(remove()) 등의 작업을 수행할 수 있다.
중복된 데이터를 허용하며, 자료의 주소 값으로 서로 연결되어 저장되어 있다. 즉, 순차적으로 접근이 가능하다.

ArrayList와 달리 배열과 LinkedList는 구조부터가 다르게 구성되어 있다. 따라서, 별개로 비교하지 않고 넘어가도록 하겠다.

LinkedList의 시간 복잡도

주요 메소드들에 따라 시간 복잡도의 차이가 있다.

1. get(int index)

특정 위치에 해당하는 데이터를 리턴한다.

시간 복잡도 : O(n)

LinkedList는 노드들이 메모리 상에 연속적으로 위치하지 않으므로, 특정 위치에 접근하려면 처음이나 끝에서부터 순차적으로 찾아가야 한다. 따라서 시간 복잡도는 O(n)이다.

2. getFirst(), getLast()

첫 번째 및 마지막 데이터를 리턴한다.

시간 복잡도 : O(1)

3. add(Object o)

LinkedList의 끝에 데이터를 추가한다.

시간 복잡도 : O(1)

4. add(int index, E element)

특정 위치에 데이터를 삽입한다.

시간 복잡도 : O(n/2) = O(n)

5. addFirst(Object o), addLast(Object o)

첫 번째와 마지막에 데이터를 추가한다.

시간 복잡도 : O(1)

6. remove()

첫 번째 데이터를 삭제하고 리턴한다.

시간 복잡도 : O(1)

7. remove(int index)

매개 변수에 지정된 위치에 있는 데이터를 삭제하고 리턴한다.

시간 복잡도 : O(n)

하지만 remove(int index) 메소드를 호출할 때, 내부적으로 LinkedList가 최적화를 진행한다.

위 내용은 아래의 링크에서 OpenJDK 프로젝트의 'java.util.LinkedList' - 'remove(int index)' 메소드 구현에서 직접 확인할 수 있다.

https://hg.openjdk.org/jdk/jdk/file/tip/src/java.base/share/classes/java/util/LinkedList.java

또는 github - openjdk 레포의 LinkedList.java 파일에서 직접 확인할 수 있다.

https://github.com/openjdk/jdk/blob/master/src/java.base/share/classes/java/util/LinkedList.java

최적화 관련 코드와 내용은 다음과 같다.

 Node<E> node(int index) {
        // assert isElementIndex(index);

        if (index < (size >> 1)) {
            Node<E> x = first;
            for (int i = 0; i < index; i++)
                x = x.next;
            return x;
        } else {
            Node<E> x = last;
            for (int i = size - 1; i > index; i--)
                x = x.prev;
            return x;
        }
    }

1) 먼저, 중간 인덱스를 찾는다.

size >> 1 // size / 2와 동일

2) 메소드는 리스트의 중간 인덱스를 기준으로 삭제할 노드가 앞에 있는지, 뒤에 있는지 판단한다.

if (index < (size >> 1)) {
..
} else {
  ..
  }

2-1) 이때, 인덱스가 리스트의 절반보다 작으면, 리스트의 시작부터 탐색을 시작한다.

index < (size >> 1) // 참일 경우, if문 수행

2-2) 반면 절반보다 크거나 같으면 리스트의 끝에서부터 탐색을 시작한다.

index < (size >> 1) // 거짓일 경우, else문 수행

2) 탐색 방향에 따라 이전 노드와 다음 노드의 참조를 갱신한다.
3) 연결이 끊긴 노드는 GC에 의해 처리되며 리스트의 크기를 줄인다.

따라서 remove(int index)의 시간 복잡도는 O(n/2)이지만, 빅-오 표기법에서 상수를 무시하기 때문에 O(n)으로 표기한다.

(추가) 소스 코드를 자세히 살펴본 결과, get(int index) 메소드와 add(int index, E element) 메소드 또한 내부에서 최적화를 진행한다.

먼저, get(int index) 메소드의 최적화 관련 코드를 살펴보자.

위 내용은 아래의 링크에서 OpenJDK 프로젝트의 'java.util.LinkedList' - 'get(int index)' 메소드 구현에서 직접 확인할 수 있다.

https://hg.openjdk.org/jdk/jdk/file/tip/src/java.base/share/classes/java/util/LinkedList.java

public E get(int index) {
    checkElementIndex(index);
    return node(index).item;
}

// ...

Node<E> node(int index) {
    // assert isElementIndex(index);

    if (index < (size >> 1)) {
        Node<E> x = first;
        for (int i = 0; i < index; i++)
            x = x.next;
        return x;
    } else {
        Node<E> x = last;
        for (int i = size - 1; i > index; i--)
            x = x.prev;
        return x;
    }
}

먼저, 전달된 인덱스가 유효한 요소 인덱스인지 확인한다.
(이때, 인덱스는 0 이상이고 리스트의 크기보다 작아야 한다.)

checkElementIndex(index);

private void checkElementIndex(int index) {
    if (!isElementIndex(index))
        throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
}

private boolean isElementIndex(int index) {
    return index >= 0 && index < size;
}

인덱스가 리스트의 절반보다 작은 경우, 처음부터 검색한다.

if (index < (size >> 1)) {
        Node<E> x = first;
        for (int i = 0; i < index; i++)
            x = x.next;
        return x;
    }

인덱스가 리스트의 절반보다 작지 않다면, 끝에서부터 검색한다.

else {
        Node<E> x = last;
        for (int i = size - 1; i > index; i--)
            x = x.prev;
        return x;
    }

다음으로 add(int index, E element) 메소드의 최적화 관련 코드를 살펴보자.

위 내용은 아래의 링크에서 OpenJDK 프로젝트의 'java.util.LinkedList' - 'add(int index, E element)' 메소드 구현에서 직접 확인할 수 있다.

https://hg.openjdk.org/jdk/jdk/file/tip/src/java.base/share/classes/java/util/LinkedList.java

public void add(int index, E element) {
    checkPositionIndex(index);

    if (index == size)
        linkLast(element);
    else
        linkBefore(element, node(index));
}

// ...

void linkBefore(E e, Node<E> succ) {
    // assert succ != null;
    final Node<E> pred = succ.prev;
    final Node<E> newNode = new Node<>(pred, e, succ);
    succ.prev = newNode;
    if (pred == null)
        first = newNode;
    else
        pred.next = newNode;
    size++;
    modCount++;
}

인덱스가 유효한 위치 인덱스인지 확인한다.
(이때, 인덱스는 0 이상이고 리스트의 크기 이하여야 한다.)

checkPositionIndex(index);

private void checkPositionIndex(int index) {
        if (!isPositionIndex(index))
            throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
    }
    
private boolean isPositionIndex(int index) {
        return index >= 0 && index <= size;
    }

인덱스가 리스트의 절반보다 작거나 큰 경우, node(int index) 메소드를 통해 노드를 반환한다.

else
    linkBefore(element, node(index));

반환된 노드는 linkBefore() 메소드의 두 번째인 인자인 succ로 전달되며, 이 메소드 내에서 새로운 요소를 적절한 위치에 연결한다.

void linkBefore(E e, Node<E> succ) {
    // assert succ != null;
    final Node<E> pred = succ.prev;
    final Node<E> newNode = new Node<>(pred, e, succ);
    succ.prev = newNode;
    if (pred == null)
        first = newNode;
    else
        pred.next = newNode;
    size++;
    modCount++;
}

이때, 인덱스가 리스트와 같은 경우 마지막 위치에 원소를 추가한다.

if (index == size)
    linkLast(element);

위와 같은 과정을 통해 get(int index) 메소드와 add(int index, E element) 메소드도 최적화를 수행한다.

✏️ 또한, get(int index) - checkElementIndex(int index)와 add(int index, E element) - checkPositionIndex(int index)는 다르다.

두 메소드 모두 인덱스가 유효한 원소 또는 위치 인덱스인지 확인하는 건 같지만 범위가 약간 다르다.

다음 예시를 통해 살펴보자.

ex. LinkedList에 5개의 요소(원소)가 있을 경우

1. checkElementIndex(int index)

유효한 원소 인덱스는 0부터 4까지이며, 이 범위를 벗어나는 인덱스는 유효하지 않다.

2. checkPositionIndex(int index)

유효한 위치 인덱스는 0부터 5까지이며, 이 범위를 벗어나는 인덱스는 유효하지 않다.

즉, checkPositionIndex(int index)의 경우 리스트의 마지막 위치에 원소를 추가할 수 있도록 인덱스의 범위가 하나 더 크다는 것이다.

이렇게 구현된 이유는 원소를 삽입하는 경우, 새로운 원소가 기존 원소의 뒤에 추가될 수 있어야 하기 때문이다.

8. remove(Object o)

매개 변수로 넘겨진 객체와 동일한 데이터 중 앞에서부터 가장 처음에 발견된 데이터를 삭제한다.

시간 복잡도 : O(n)

9. removeFirst(), removeLast()

첫 번째와 마지막 데이터를 삭제하고 리턴한다.

시간 복잡도 : O(1)

Stack vs Queue

이러한 ArrayList와 LinkedList 클래스는 모두 List 인터페이스를 구현한 것이다.

즉, List 인터페이스에는 ArrayList, LinkedList뿐만 아니라 Vector와 Stack이라는 클래스가 추가로 존재한다.

Vector와 Stack 클래스에 대해서 짧게 설명하자면 다음과 같다.

Vector

ArrayList와 사용법도 거의 동일하고 기능도 거의 비슷하지만, ArrayList는 JDK 1.2부터 추가된 반면 Vector 클래스는 JDK 1.0부터 존재했다.

또한, ArrayList는 Thread safe하지 않은 반면 Vector는 Thread safe하다.

Stack

Vector 클래스를 확장하여 만들었으며 LIFO(List-In First-Out) 구조를 가지고 있다.

즉, 가장 마지막에 추가한 값을 가장 먼저 빼내는 구조이다.

대표적인 예시로 카드 스택을 생각하면 카드가 쌓인 모습이 떠오를 것이다. 그 모습이 stack과 같다고 생각하면 된다. 📚

Queue

Queue는 Stack과 달리 FIFO(First-In First-Out) 구조를 가지고 있다.

즉, 가장 처음에 추가한 값을 가장 먼저 빼내는 구조이다.

대표적인 예시로 기차를 생각하면 된다. 기차는 칸과 칸이 연결기라고 하는 매개체로 연결되어 있다. 🚃

그래서 Stack, Queue는 ArrayList, LinkedList와 어떤 상관이 있지?

위에서 Queue를 기차에 비유해서 설명할 때, LinkedList와 유사하다는 생각이 들었을 것이다.

결론적으로 Queue는 FIFO 용도로 사용하기 때문에 Queue를 구현할 때, LinkedList로 구현한다.

노드를 동적으로 추가 및 삭제가 가능하기 때문에, 첫 번째 데이터의 삽입 및 삭제 작업이 효율적이다.

반대로 Stack을 구현할 때는 LIFO 원칙에 따라 ArrayList로 구현한다.

마지막 요소에 빠르게 접근하여 삽입 및 삭제를 수행할 수 있다.
이는 ArrayList가 내부적으로 배열을 사용하여 인덱스 기반 액세스가 빠르기 때문이다.

단, 위의 설명은 일반적인 경우이고 각각의 상황(ex. ArrayList의 배열 크기 조절 작업이 필요한 경우)과 요구 사항에 따라 구현할 자료구조는 달라질 수 있다.

정리

ArrayList

내부적으로 Object 타입의 배열([ ]) 구조로 구성되어 있으며 인덱스를 기반으로 각각의 요소(element)에 접근하여 검색(get()), 추가(add()), 삭제(remove()) 등의 작업을 수행할 수 있다.

LinkedList

내부적으로 노드와 포인터(=링크)를 가진 구조로 구성되어 있으며, 포인터를 통해 각각의 노드에 접근하여 검색(get()), 추가(add()), 삭제(remove()) 등의 작업을 수행할 수 있다.

ArrayList vs LinkedList

ArrayList는 내부적으로 배열 구조를 가지고 있는 반면, LinkedList는 내부적으로 노드와 포인터 구조로 이루어져 있다.
ArrayList는 인덱스를 통해 빠르게 검색할 수 있는 반면, LinkedList는 처음 또는 끝에서부터 순차적으로 검색을 수행해야 한다.
ArrayList는 중간에 데이터를 추가 또는 삭제 시, 그 위치 이후의 데이터들을 한 칸씩 앞으로 이동시켜야 하므로 시간 복잡도는 O(n)이다. 반면, LinkedList는 데이터를 추가 또는 삭제시, 이전 노드와 이후 노드의 포인터만 다시 연결하면 되므로 작업 자체의 시간 복잡도는 O(1)이다. (물론, 데이터를 탐색한 후 추가 또는 삭제하는 상황이라면 시간 복잡도는 동일하게 O(n)이 걸린다.)

ArrayList와 LinkedList는 비슷한듯 보이지만, 실상은 다른 자료구조 클래스이다.

Eunbi Lee

B - B = 이은비

이전 포스트

[Java] ArrayList vs LinkedList

Java

Collection이란?

📚 ArrayList란?

ArrayList의 특징

Obejct 클래스 타입의 배열 vs ArrayList

ArrayList의 시간 복잡도

1. get(int index)

2. add(E element)

3. add(int index, E element)

4. remove(int index)

5. remove(Object o)

🚃 LinkedList란?

LinkedList의 특징

LinkedList의 시간 복잡도

1. get(int index)

2. getFirst(), getLast()

3. add(Object o)

4. add(int index, E element)

5. addFirst(Object o), addLast(Object o)

6. remove()

7. remove(int index)

(추가) 소스 코드를 자세히 살펴본 결과, get(int index) 메소드와 add(int index, E element) 메소드 또한 내부에서 최적화를 진행한다.

✏️ 또한, get(int index) - checkElementIndex(int index)와 add(int index, E element) - checkPositionIndex(int index)는 다르다.

1. checkElementIndex(int index)

2. checkPositionIndex(int index)

8. remove(Object o)

9. removeFirst(), removeLast()

Stack vs Queue

Vector

Stack

Queue

그래서 Stack, Queue는 ArrayList, LinkedList와 어떤 상관이 있지?

정리

ArrayList

LinkedList

ArrayList vs LinkedList

[자바의 신] 정리해 봅시다 (Ch 20~27)

0개의 댓글