[Java] 백준 9251번: LCS

Eunbi Lee·2024년 1월 23일

algorithm

Algorithm

목록 보기

6/7

원래 알고리즘 블로그 포스팅은 블로그 원정대의 일정에 맞춰 주 1회씩만 작성하려고 했었는데, 드디어 DP에 대한 감을 잡을 수 있었던 기념비적인 문제라 야심한 시각에 포스팅을 작성하게 되었다.

그리고 좋은 포스팅이란 무엇인가?에 대해서 생각하면서 나름의 틀을 잡고, 이전 알고리즘 포스팅보다 정리해서 글을 작성해보았다. 언제든지 피드백은 환영!

LCS

문제 설명

LCS(Longest Common Subsequence, 최장 공통 부분 수열) 문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, "ACAYKP"와 "CAPCAK"의 LCS는 "ACAK"가 된다.

입력

첫째 줄과 둘째 줄에 두 문자열이 주어진다.
문자열은 알파벳 대문자로만 이루어져 있다.
- 최대 1,000글자로 이루어져 있다.

출력

첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를 출력한다.

예제 입력 1

ACAYKP
CAPCAK

예제 출력 1

풀이

접근법은 다음과 같다.

두 문자열을 받아온다.

두 문자열의 크기 + 1을 가지는 DP라는 이름의 2차원 배열을 선언한다.

이때, dp에는 구하고자 하는 LCS의 길이를 저장한다.

i와 j라는 임시 변수를 통해 2차원 loop으로 두 문자열의 각각의 문자를 탐색한다.

이때, 두 문자가 같을 경우는 직전 행 및 열의 값(= 직전 행 && 직전 열의 값)에 + 1을 함으로써 LCS를 1 증가시킨다.

두 문자가 같지 않을 경우는 직전 행 또는 열의 값(= 직전 행 || 직전 열의 값)과 각각 비교해서 큰 값을 가져온다.(= 더 큰 LCS 값으로 업데이트)

2차원 dp 배열의 마지막 값을 출력한다.

풀이 흐름은 다음과 같다.

두 문자열의 문자들을 하나씩 가져와서 비교한다.
이때, 두 문자열의 공통 문자들을 하나씩 누적시키면서 LCS의 값을 증가시킨다.
따라서 이전 문자를 비교함으로써 누적시킨 값, 즉 LCS를 활용해야 하므로 DP를 사용해야 한다.
그렇다면 DP에는 어떤 값이 들어가야할까?
우선 자세히 보자면 LCS는 같은 문자를 두 문자열이 공통으로 가지고 있을 때의 길이이다.
또한 공통 문자는 연속적인 문자가 아니어도 된다. 즉, 예제 입력 1에서의 LCS인 "ACAK"도 떨어져 있는 문자임에도 불구하고 카운트를 진행했다.
따라서 각각 두 문자열의 모든 문자를 탐색해야 하므로 2차원 배열을 쓰도록 한다.
두 문자열의 문자를 비교할 때는 하나의 문자열을 기준으로 다른 문자열의 문자를 하나씩 비교한다.
즉, "ACAYKP"가 기준일경우 "ACAYKP"의 각 문자에 대해 차례대로 "CAPCAK"의 문자들을 순회한다.
다시 말해서, "ACAYKP"를 순회하는 기준이 i라면, i = 1일 경우(i 및 j = 0일 경우는 제외한다, 이유는 아래에서 설명) "A"에 대해 j = 1일 경우 "C"를 탐색한다.
j = 2일 경우, "A"에 대해 "A"를 탐색한다.
j = 3일 경우, "A"에 대해 "P"를 탐색한다. ..
(추가)
i = 2일 경우, "AC" 중 "C"에 대해 탐색을 이어서 진행한다..
따라서 비교하는 시점에서 두 문자열의 마지막 문자(ex. i = 1, j = 6이라면 각각 "A"와 "K"를 비교해서 일치하는지를 확인한다.
이후, 첫 번째 문자열과 두 번째 문자열의 크기만큼 초기화 및 선언된 2차원 DP 배열의 마지막 값에는 지금까지 누적된 LCS가 있을테니 해당 값을 출력해서 종료한다.

어려웠던 포인트들

왜 2차원 dp 배열을 선언해야 할까?

dp 안의 데이터는 무엇을 담고 있을까?

왜 dp 배열의 크기를 +1만큼 선언해야 할까? (= int[][] dp = new int[strSequence1.length() + 1][strSequence2.length() + 1];)

왜 문자가 같을 경우는 dp[i][j] = dp[i - 1][j - 1] + 1;으로 선언이 될까?

또, 문자가 다를 경우는 왜 dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);와 같이 선언이 될까?

적고보니 사실상 DP의 핵심 개념들을 잘 몰랐던 것 같다.

우선 각각의 질문들에 대해 정리를 해보자면 다음과 같다.

두 문자열의 모든 문자들을 비교해야 한다. 따라서, 1차원이 아닌 2차원의 배열로 선언함으로써 2중 loop문을 통해 i, j로 각각의 문자에 접근해서 비교를 진행해야 한다.
구하고자 하는 값인 LCS가 담겨져 있을 것이다. 왜냐하면 DP 배열을 통해 값을 도출해야 하니까?
음.. 사실 이 부분은 문자열의 크기만큼 선언하고 진행해도 된다. 즉,int[][] dp = new int[strSequence1.length()][strSequence2.length()];과 같이 선언하고 진행해도 된다.

하지만, 이럴 경우 아주아주 귀찮아진다.
우선 2차원 DP 배열을 선언할 경우 모양은 다음과 같은 n x n 크기의 정사각형 배열이 될 것이다.

단, 예제 입력 1의 두 문자열이 자리가 같아서 n x n으로 구성이 될 뿐.. 실제로는 첫 번째 문자열의 크기 x 두 번째 문자열의 크기이다.

0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0

이때 위와 같이 +1을 하지 않은 크기를 선언했을 경우, 이 상태에서 i - 1과 j - 1(-1을 하는 이유는 조건에 따라 이전 LCS의 값을 가져오기 위함이다.)을 가져올 때 첫 번째 행과 열에서 범위를 벗어나게 되므로 인덱스의 크기가 부족하다는 예외가 터진다.

따라서 이례적으로 첫 번째 열과 행에 1이라는 값들을 세팅해줘야 하는데,

0 1 1 1 1 1
1 0 0 0 0 0
1 0 0 0 0 0
1 0 0 0 0 0
1 0 0 0 0 0

이것이 귀찮기 때문에 그냥 +1만큼의 크기를 선언함으로써 바로 (2, 2) (= (1,1))이 원점이라는 가정 하에)부터 값을 채워나갈 수 있는 것이다.

4.와 5.는 이 문제의 핵심이다.

참고 그림은 다음과 같다.

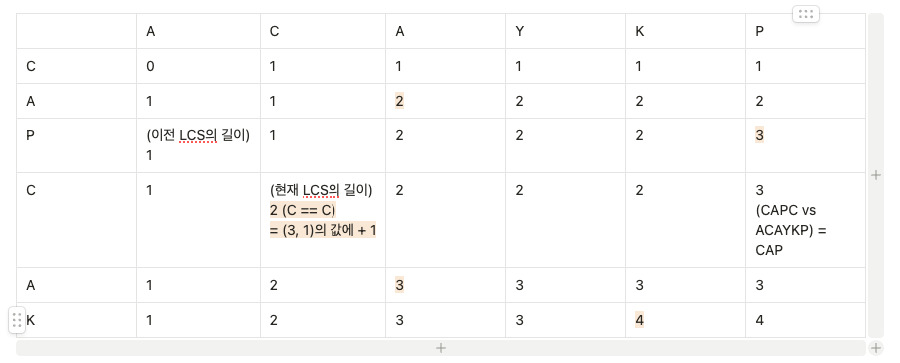
위 그림을 보면 업데이트 된 LCS값을 주황색으로 마킹해두었다.

대표적으로 현재 LCS의 길이라고 명시된 2를 보자. (= (2, 2))

해당 값은 "CAPC"와 "AC"를 비교했을 때, 누적된 LCS의 값인 2가 들어있다.

그리고 이 값은 왼쪽 대각선 상에 위치한 (1, 1)로부터 각 문자열의 문자를 하나씩 더 탐색한 위치이다. 또한, 각 문자가 동일한 순간이다.

즉, 문자가 동일한 순간이므로 dp[i][j] = dp[i - 1][j - 1] + 1;으로 표기가 되는 것이다.

반대로, 문자가 같지 않을 경우는 현재 값(= dp[i][j])을 기준으로 직전 열 또는 직전 행의 값 중 큰 값을 가져오면 되기 때문에 dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]); 으로 표기가 되는 것이다.

전체 코드

package silver.class4;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;

public class LCS {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); // 입력부터 다 처리해놓고 고민할래~
        String strSequence1 = br.readLine();
        String strSequence2 = br.readLine();

        int[][] dp = new int[strSequence1.length() + 1][strSequence2.length() + 1];

        for (int i = 1; i <= strSequence1.length(); i ++) {
            for (int j = 1; j <= strSequence2.length(); j ++) {
                if (strSequence1.charAt(i - 1) == strSequence2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        System.out.println(dp[strSequence1.length()][strSequence2.length()]);
        br.close();
    }
}