Game Programming in C++ - Day 13

이응민·2024년 9월 11일

Game Programming in C++

목록 보기

13/21

Day 13 스프라이트의 변환

변환 기초

게임의 주변을 돌아다니는 10개의 운석이 있다고 하면 이 10개의 운석은 각각 다른 버텍스 배열 개체로 나타낼 수 있다. 이러한 버텍스 배열 개체는 화면상에서 운석을 다른 위치에 나타내기 위해 필요하며, 이는 각 운석을 그리기 위한 삼각형이 다른 NDC(정규화된 장치 좌표)를 필요로 한다는 것을 의미한다. 가장 간단한 방법은 10개의 다른 버텍스 버퍼를 생성하고 각 버텍스 버퍼를 하나의 운석에 대응시킨 뒤 이 버텍스 버퍼를 필요에 따라 재계산하는 것이다. 하지만 이렇게 하면 계산 측면이나 메모리 사용 측면에서 낭비가 심하다. 버텍스 버퍼의 버텍스를 변경하고 변경된 내용을 OpenGL에 다시 알리는 것은 효율적이지 못하다. 대신 추상적인 관점에서 스프라이트를 생각해보면 모든 스프라이트는 궁극적으로 사각형일 뿐이다. 여러 스프라이트는 화면상의 위치가 다를 수 있고 크기나 회전값도 다를 수 있지만 그래도 스프라이트는 사각형이다. 스프라이트를 이런 관점에서 생각한다면 효율적인 해결책은 사각형에 대해서는 버텍스 버퍼를 하나만 가지고 이 버텍스 버퍼를 재활용하는 것이다. 사각형을 그릴 시에는 NDC 단위 사각형을 활용해서 스프라이트를 임의의 위치, 크기, 방향을 가진 사각형으로 변경하거나 변환(transform)하면 된다. 한 유형의 오브젝트에 대해 하나의 버텍스 버퍼만을 재사용하는 방법은 3D에도 확장해서 적용가능하다.

오브젝트 공간

3D 모델링 프로그램을 사용해서 3D 오브젝트를 만들 때 일반적으로 정규화된 장치 좌표로 버텍스 위치를 나타내지 않는다. 대신 위치는 오브젝트 그 자체의 임의의 원점에 상대적이다. 이 원점은 보통 오브젝트의 중심에 해당한다. 이 오브젝트 그 자체에 대한 상대적인 좌표 공간을 오브젝트 공간(object space) 또는 모델 공간(model space)라고 한다. 좌표 공간을 정의하려면 좌표 공간의 원점과 좌표 요소가 증가하는 방향(기저 벡터)가 필요하다. 예를 들어 일부 3D 모델링 프로그램은 +y를 위 방향으로 사용하지만, 다른 프로그램에서는 +z를 위 방향으로 사용한다. 이러한 서로 다른 기저 벡터는 서로 다른 오브젝트 공간을 정의한다.

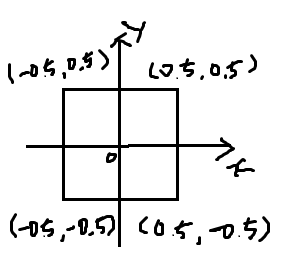
위 그림은 원점이 오브젝트 공간의 중심이고 +y는 위로 증가하고 +x는 오른쪽으로 증가하는 2D 사각형이다. 게임은 다양한 모델이 필요할 것이다. 각각의 모델은 자신만의 오브젝트 공간에서 생성할 수 있으며 이는 각 오브젝트의 버텍스 위치가 해당 모델 고유의 오브젝트 공간 원점에 상대적이라는 걸 뜻한다. 게임을 실행하면 각각의 고유의 모델은 자신의 버텍스 배열 개체(VAO, Vertex Array Object)에 로드된다. 게임은 각각 모델의 VAO를 가진다. 그리고 장면을 그릴 때 각 오브젝트의 버텍스는 버텍스 셰이더로 전달된다. Basic.vert처럼 버텍스 위치를 수정없이 직접 프래그먼트 셰이더에 넘긴다면 이 버텍스 위치는 정규화된 장치 좌표가 될 것이다. 하지만 직접 넘긴 버텍스 모델 좌표는 NDC가 아니고 각 오브젝트 공간에 상대적인 좌표이므로 문제가 된다. 그래서 버텍스 셰이더에서 버텍스의 위치를 그대로 통과시키면 의미없는 출력만을 얻는다.

세계 공간

여러 오브젝트들이 다른 오브젝트 공간 좌표를 갖는 문제를 해결하려면 먼저 게임 세계 그 자체에 대한 좌표 공간을 정의해야한다. 세계 공간(world space)이라고 불리는 이 좌표 공간은 자신만의 원점과 기저 벡터를 갖고 있다. 게임 상의 오브젝트는 세계 공간 원점에 상대적인, 임의의 위치와 크기, 방향을 가진다. 게임에서 같은 오브젝트의 각 인스턴스를 그릴 때는 같은 버텍스 배열 개체를 사용한다. 그러나 이제 각 인스턴스는 오브젝트 공간 좌표를 세계 공간으로 변환하는 방법은 지정하는 추가적인 정보가 더 필요하다. 이 여분의 데이터는 인스턴스를 그릴 때 버텍스 셰이더로 보낼 수 있으며, 버텍스 셰이더가 필요에 따라 버텍스 좌표를 보정하는데 쓰인다. 물론 그래픽 하드웨어는 버텍스 위치를 그리기 위해 NDC 좌표를 필요로 하므로 버텍스를 세계 공간으로 변환한 후에도 추가적인 단계가 더 필요하다.

세계 공간으로 변환

좌표 공간을 변환할 때는 두 좌표 공간 사이에 기저 벡터가 같은지 또는 그렇지 않은지를 알아야한다. 예를 들어 오브젝트 공간의 점 (0, 5)를 고려해 보자. 오브젝트 공간에서 +y를 위 방향으로 정의한다면 점 (0, 5)는 원점에서 다섯 단위 위에 있다는 것을 뜻한다. 그러나 세계 공간에서 +y가 오른쪽 방향이라면 점 (0, 5)는 원점에서 오른쪽 방향이라면 점 (0, 5)는 원점에서 오른쪽으로 다섯 단위 떨어진 곳에 놓이게 된다. 여기서 사용된 2D 좌표 체계는 +y가 아래 방향인 SDL 좌표 체계와 다르다.

세계 공간의 원점은 게임 창의 중심이라고 할 수 있다.목표는 위 그림에서처럼 오브젝트 공간을 갖는 단위 사각형을 세계 공간의 원점을 기준으로 임의의 위치와 크기 그리고 방향을 가진 사각형으로 표현하는 것이다. 예를 들어 사각형의 한 인스턴스가 세계 공간에서는 크기가 2배이고 세계 공간 원점의 오른쪽 방향으로 50단위 떨어져서 나타나야한다고 했을때 사각형의 각 버텍스에 수학 연산을 적용하면 이 목표를 달성할 수 있다. 한 가지 방법은 정확한 버텍스의 위치를 계산하기 위해 대수 방정식을 사용하는 것이다.

이동(translation)
이동은 점을 변환시키거나 오프셋 값으로 이동시킨다. 점 $(x, y)$ 가 주어졌을 때 다음 방정식을 이용하면 오프셋 $(a, b)$ 만큼 점을 이동시킬 수 있다.

$x^{'} = x + a$
$y^{'} = y + b$

삼각형의 모든 버텍스에 같은 이동을 적용하면 삼각형의 이동이 가능해진다.

스케일(scale)
스케일을 삼각형의 각 버텍스에 적용하면 삼각형의 크기는 커지거나 작아진다. 균등 스케일(uniform scale)에서는 버텍스의 각 요소에 같은 스케일 팩터 $s$ 를 사용해서 스케일한다.

$x^{'} = x \cdot s$
$y^{'} = y \cdot s$

삼각형의 각 버텍스를 5배 스케일링하면 삼각형의 크기는 5배 커진다. 비균등 스케일(non-uniform scale)에서는 각 요소에 대해 별도에 스케일 팩터 $(s_x, s_y)$ 를 곱한다.

$x^{'} = x \cdot s_x$
$y^{'} = y \cdot s_y$

단위 사각형을 변환하는 경우 비균등 스케일은 정사각형 대신에 직사각형을 만든다.

회전(rotation)
단위 원은 점 (1, 0)에서 시작한다. 90도 또는 $\pi\over 2$ 라디안 회전은 점 (0, 1)로의 반시계 방향 회전이며, 180도 또는 $\pi$ 라디안 회전은 점 (-1, 0)이 된다. 이 회전은 비록 일반적인 단위 원 다이어그램에서 z축을 그리지 않는다 하더라도 기숙적으로 z축에 대한 회전이다. 사인과 코사인을 사용하면 다음과 같이 임의의 점 $(x, y)$ 를 각도 $\theta$ 만큼 회전시키는 공식은 다음과 같다.

$x^{'} = xcos\theta - ysin\theta$
$y^{'} = xsin\theta + ycos\theta$

방정식 $x$ 와 $y$ 값에 의존한다. 단위 원에서 처럼 각도 $\theta$ 는 반시계 회전을 나타낸다. 이 회전은 원점을 기준으로 한 회전이다. 오브젝트 공간 원점 중심에 삼각형이 놓인 경우, 각 버텍스를 회전하면 삼각형은 원점을 중심으로 회전한다.

변환을 결합
앞의 수식들은 각 변환을 독립적으로 적용하지만 동일한 버텍스에 대해서는 여러 변환을 동시에 적용하는 것이 일반적이다. 예를 들어 사각형이 있다면 이 사각형을 이동시키고 회전시키는 작업 둘 다 필요할 수 있다. 이러한 변환들을 적용할 때는 올바른 순서로 결합하는것이 중요하다. 변환 순서가 중요하므로 일관성 있는 순서를 갖는 것이 가장 중요하다. 오브젝트 공간에서 세계 공간으로의 변환에서는 항상 스케일, 회전, 이동 순으로 변환을 적용한다. 이를 방정식으로 아래 식과 같이 표현할 수 있다.

$x^{'} = s_x\cdot xcos\theta - s_y\cdot ysin\theta + a$
$y^{'} = s_x\cdot xsin\theta + s_y\cdot ycos\theta + b$

방정식의 통합에 따른 문제
오브젝트 공간에서 임의의 버텍스를 얻어서 각 요소에 방정식을 적용하면 세계 공간으로 변환된 임의의 스케일, 회전, 위치를 가진 버텍스를 얻을 수 있었다. 하지만 이 작업은 오직 버텍스를 오브젝트 공간에서 세계 공간으로 변환만 할 뿐이다. 세계 공간의 좌표는 장치 좌표에 대해 정규화돼 있지 않으므로 여전히 버텍스 셰이더에서는 많은 변환을 적용해야한다. 이 추가적인 변환은 일반적으로 지금까지 설명한 방정식처럼 간단한 것이 없다. 간단하지 않은 이유는 여러 좌표 체계 사이의 기저 벡터가 다르기 때문이다. 이러한 추가 변환을 하나의 방정식으로 결합해버리면 복잡성이 증가한다. 이 문제에 대한 해결책은 각 요소에 대해 별도의 방정식을 사용하지 않고 대신 행렬을 사용해 여러 변환을 표현하는 것이다. 여러 변환은 행렬 곱셈으로 쉽게 결합할 수 있다.

행렬과 변환

행렬(matrix)는 m행과 n열이 있는 값의 격자다. 예를 들어 $2\times2$ 행렬은 다음과 같이 a에서 d값을 가지는 행렬로 표현하는 것이 가능하다.

$\begin{bmatrix}a&b\\c&d\\ \end{bmatrix}$

컴퓨터 그래픽스 분야에서는 행렬을 사용해서 변환을 표현한다. 스케일링, 이동, 회전 모두 해당 변환에 대응하는 행렬 표현이 존재한다.

행렬 곱셈

스칼라와 마찬가지로 두 행렬은 서로 곱할 수 있따. 다음 행렬이 있다고 가정하자.

$\begin{bmatrix}a&b\\c&d\\ \end{bmatrix}$ $\begin{bmatrix}e&f\\g&h\\ \end{bmatrix}$

곱셈 $C=AB$ 의 결과는 다음과 같다.

$C=AB=$ $\begin{bmatrix}a&b\\c&d\\ \end{bmatrix}$ $\begin{bmatrix}e&f\\g&h\\ \end{bmatrix}$ $=$ $\begin{bmatrix}a\cdot e + b\cdot g&a\cdot f + b\cdot h\\c\cdot e + d\cdot g&c\cdot f + d\cdot h\\ \end{bmatrix}$

즉 C의 왼쪽 위 요소는 A의 첫 번째 행과 B의 첫 번째 열과의 내적이다. 행렬 곱셈은 같은 차원을 가진 행렬을 요구하지 않는다. 하지만 왼쪽 행렬의 열의 수는 오른쪽 행렬의 행의 수와 같아야한다. 예를 들어 다음 곱셈은 유효한 곱셈이다.

$\begin{bmatrix}a&b\\ \end{bmatrix}$ $\begin{bmatrix}c&d\\e&f\\ \end{bmatrix}$ = $\begin{bmatrix}a\cdot c+b\cdot e&a\cdot d+b\cdot f\\ \end{bmatrix}$

행렬 곱셈은 결합은 가능하지만 교환은 가능하지 않다.

$AB\neq BA$
$A(BC)=(AB)C$

행렬을 이용한 점의 이동

변환 측면에서 보면 행렬은 임의의 점으로 표현하는 것이 가능하다. 예를 들어 점 $p=(x, y)$ 는 하나의 행(행 벡터, row vector)으로 나타낼 수 있다.

$p=\begin{bmatrix}x&y\\ \end{bmatrix}$

또한 하나의 열(열 벡터, column vector)로 나타낼 수 있다.

$p=\begin{bmatrix}x\\y\\ \end{bmatrix}$

행 벡터로 표현하든 열 벡터로 표현하든 문제는 없지만, 일관된 하나의 방식을 사용하는 것이 중요하다. 그 이유는 점이 행인지 열인지에 따라 벡터가 곱셉의 왼쪽 또는 오른쪽에 위치될지가 결정되기 때문이다. 여기 변환 행렬 $T$ 가 있다.

$T=\begin{bmatrix}a&b\\c&d\\ \end{bmatrix}$

행렬 곱셈을 이용하면 이 행렬로 점 $p$ 를 변환해서 변환된 점 $(x^{'},y^{'})$ 를 얻을 수 있다. 하지만 $p$ 가 행일 때 T를 곱한 결과와 $p$ 가 열일 때 $T$ 를 곱한 결과는 서로 다르다. $p$ 가 행이라면 곰셈은 다음과 같다.

$T=\begin{bmatrix}x^{'}&y^{'}\\ \end{bmatrix}$ $=pT=$ $\begin{bmatrix}x&y\\ \end{bmatrix}$ $\begin{bmatrix}a&b\\c&d\\ \end{bmatrix}$
$x^{'}=a\cdot x + c\cdot y$
$y^{'}=b\cdot x + d\cdot y$

하지만 $p$ 가 열이라면 다음과 같은 결과를 산출한다.

$\begin{bmatrix}x^{'}\\y^{'}\\ \end{bmatrix}$ $=Tp=$ $\begin{bmatrix}a&b\\c&d\\ \end{bmatrix}$ $\begin{bmatrix}x\\y\\ \end{bmatrix}$
$x^{'}=a\cdot x + b\cdot y$
$y^{'}=c\cdot x + d\cdot y$

이 곱셈은 $x^{'}$ 와 $y^{'}$ 대해 2가지 다른 값을 돌려주지만, 오직 하나만이 올바른 해답이다. 변환 행렬의 올바른 계산은 행 벡터 또는 열 벡터의 사용 여부에 달려있기 때문이다. 행 벡터 또는 열 벡터의 사용 여부는 리소스나 그래픽 API에 따라 행 벡터 또는 열 벡터를 사용한다. 변환이 주어진 점에 대해 왼쪽에서 오른쪽 순으로 적용되기 때문에 행 벡터를 주로 사용한다. 다음 방정식은 $q$ 를 먼저 행렬 $T$ 로 변환한다. 그런 다음 행렬 $R$ 로 변환시킨다.

$q^{'}=qTR$

각 변환 행렬에 트랜스포즈(transpose)를 적용하면 행 벡터를 열 벡터로, 열 벡터를 행 벡터로 전환하는 것이 가능하다. 행의 트랜스포즈는 원래 행렬의 첫 번째 행이 결과 행렬의 첫 번째 열이 되도록 행렬을 회전시킨다.

$\begin{bmatrix}a&b\\c&d\\ \end{bmatrix}^T=\begin{bmatrix}a&c\\b&d\\ \end{bmatrix}$

점 $q$ 를 열 벡터로 사용한 방정식을 전환하길 원한다면 다음과 같이 계산하면 된다.

$q^{'}=R^TT^Tq$

마지막으로 항등 행렬(identity matrix)은 대문자 $I$ 로 표현되는 특별한 유형의 행렬이다. 항등 행렬은 같은 수의 행과 열을 가진다. 항등 행렬에서 모든 값은 대각선을 제외하고 0이다. 대각선 값은 모두 1이다. 예를 들어 $3\times 3$ 항등 행렬은 다음과 같다.

$I_3=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\\ \end{bmatrix}$

항등 행렬을 임의의 행렬과 곱하면 행렬은 변경되지 않느다. 즉 다음과 같다.

$MI = M$

세계 공간으로 변환, 재검토

행렬로 스케일, 회전, 이동 변환을 표현하는 것이 가능하다. 변환을 결합한 통합 방정식을 유도하는 대신 행렬을 서로 곱하자. 결합된 세계 변환 행렬을 얻으면 이 세계 변환 행렬로 오브젝트의 모든 버텍스를 세계 공간으로 변환하는 것이 가능해진다.

스케일 행렬
스케일 변환을 적용하기 위해 $2\times2$ 스케일 행렬을 사용한다.

$\begin{bmatrix}s_x&0\\0&s_y\\ \end{bmatrix}$

회전 행렬
2D 회전 행렬은 $\theta$ 로 $z$ 축에 대한 회전을 나타낸다.

$R(\theta)=\begin{bmatrix}cos\theta&sin\theta\\-sin\theta&cos\theta\\ \end{bmatrix}$

이동 행렬
$2\times2$ 행렬은 2D 스케일 및 회전 행렬의 표현이 가능하지만 $2\times2$ 크기로는 일반적인 2D 이동 행렬을 표현할 방법이 없다. 이동 $T(a, b)$ 를 표현하는 유일한 방법은 이동 행렬을 $3\times3$ 행렬로 표현하는 것이다.

$T=\begin{bmatrix}1&0&0\\0&1&0\\a&b&1\\ \end{bmatrix}$

그러나 $1\times2$ 행렬은 충분한 열을 가지고 있지 않으므로 점을 나타내는 $1\times2$ 행렬과 $3\times3$ 행렬을 곱할 수 없다. 행 벡터에 추가 열을 더해서 $1\times3$ 행 벡터로 만들어야 두 행렬을 곱할 수 있다. 이를 위해 점에 추가 요소를 더한다. 동차(homogenous) 좌표는 $n$ 차원 공간을 나타내기 위해 $n + 1$ 요소를 사용한다. 그래서 2D 공간에서 동차 좌표는 3개의 요소를 사용한다. 이 세 번째 요소를 w 요소라고 한다. 그래서 동차 좌표로 나타낸 2D 점은 $(x, y, w)$ 이며 동차 좌표로 표현된 3D 점은 $(x, y, z, w)$ 이다. 지금은 w 요소에 1만을 사용할 것이다. 예를 들어 $p(x, y)$ 는 동차 좌표 $(x, y, 1)$ 로 표현된다. 이동 행렬을 곱하더라도 동차 좌표에서 w 요소는 그대로 1을 유지한다. 하지만 x, y 요소는 원하는만큼 이동한다.

변환 결합
여러 변환 행렬은 서로 곱해서 결합하는 것이 가능하다. 그러나 $2\times 2$ 행렬에 $3\times 3$ 행렬을 곱할 수 없다. 그러므로 스케일 및 회전 변환을 동차 좌표로 동작하는 $3\times 3$ 행렬로 표현해야한다.

$S(s_x, s_y)=\begin{bmatrix}s_x&0&0\\0&s_y&0\\0&0&1\\ \end{bmatrix}$
$R(\theta)=\begin{bmatrix}cos\theta&sin\theta&0\\-sin\theta&cos\theta&0\\0&0&1\\ \end{bmatrix}$

이제 크기, 회전, 이동 변환 행렬을 $3\times 3$ 행렬로 표현했으므로 이를 결합해서 하나의 변환 행렬을 만들 수 있다. 오브젝트 공간에서 세계 공간으로 변환하는 이 결합 행렬은 세계 변환 행렬(world transform matrix)이다. 세계 변환 행렬을 계산하기 위해 스케일, 회전, 이동 행렬을 다음과 같은 순서로 곱한다.

$WorldTransform=S(s_x, s_y)R(\theta)T(a, b)$

이 곱셈 순서는 변환을 적용하려는 순서와 일치한다. 이렇게 얻은 세계 변환 행렬을 버텍스 셰이더에 전달하고 오브젝트의 모든 버텍스를 전달된 세계 변환 행렬로 변환시킨다.

세계 변환을 액터에 추가

Actor 클래스의 정의에는 이미 위치에 대한 Vector2와 스케일에 대한 float, 그리고 각도 회전에 대한 float 값이 이미 존재한다. 이제 이 다양한 속성을 세계 변환 행렬 속으로 결합해야한다. 먼저 Actor 클래스에 Matrix4와 bool 2개의 멤버 변수를 추가한다.

Matrix4 mWorldTransform;
bool mReComputeWorldTransform;

mWorldTransform 변수는 세계 변환 행렬을 저장한다. Matrix3 대신에 Matrix4를 사용하는 이유는 버텍스 레이아웃에서 모든 버텍스가 z 요소도 있다고 가정했기 때문이다. bool 변수는 세계 변환 행렬을 재계산할 필요가 있는지를 저장한다. 액터의 위치, 스케일, 회전에 대한 각 setter 함수에서 mRecomputeWorldTransform 값을 true로 설정해야한다. 이런 방식으로 각 요소의 속성이 변경되면 세계 변환 행렬을 다시 계산해야한다. 또한 생성자에서 mRecomputeWorldTransform 값을 true로 초기화 해서 각 액터가 적어도 한 번은 세계 변환 행렬 계산을 하도록 보장해야한다. 그리고 다음과 같이 CreateWorldTransform 함수를 구현한다.

CreateScale은 균등 스케일 행렬을 생성하며 CreateRotationZ는 z축에 대한 회전 행렬을 생성한다. 그리고 CreateTranslation은 이동 행렬을 만든다. Actor::Update 에서는 컴포넌트가 업데이트 전에 ComputeWorldTransform을 한 번 호출하고 UpdateActor를 호출한 후 ComputeWorldTransform을 한 번 더 호출한다.

그런 다음 Game::UpdateGame에서는 '대기중인'액터가 올바른 세계 변환을 가지도록 ComputeWorldTransform의 호출을 추가한다.

소유자(Actor)의 세계 변환이 갱신될 때 컴포넌드에게 통지할 수 있는 방법이 있다면 좋을 것이다. 통지 방법을 구현하면 컴포넌트는 상황에 따른 반응이 가능해진다. 이를 지원하기 위해 기본 컴포넌트 클래스에 가상 함수를 추가한다.

virtual void OnUpdateWorldTransform() { }

다음으로 ComputeWorldTransform 함수 내부에서 액터 컴포넌트 각각에 대해 OnUpdateWorldTransform 함수를 호출한다. 이제 액터는 세게 변환 행렬을 저장한다.

세계 공간에서 클립 공간으로 변환하기

세계 변환 행렬을 사용하면 버텍스를 세계 공간으로 변환할 수 있다. 다음 단계는 버텍스를 버텍스 셰이더가 원하는 출력인 클립 공간(clip space)으로 변환하는 것이다. 클립 공간은 정규화된 장치 좌표에 가까운 친척에 해당한다. 유일한 차이점은 클립 공간이 w 요소를 갖고 있다는 데 있다. 이 때문에 gl_Position 변수는 버텍스 위치를 저장하기 위해 vec4로 선언됐다. 뷰-투영 행렬(view-projection matrix)은 세계 공간을 클립 공간으로 변환시킨다. 이름에서 알 수 있듯 뷰-투영 행렬은 뷰 행렬과 투영 행렬, 2개 가진다. 뷰는 가상 카메라가 게임 세계를 바라보는 방법으로 설명하며, 투영 행렬은 가상 카메라의 시점으로 부터 크립 공간으로 변환하는 방법을 지정한다. 정규화된 장치 좌표에서는 화면의 왼쪽 하단이 (-1, -1)이고 오른쪽 상단이 (1, 1)이다. 그리고 화면 스크롤이 없는 2D 게임이라고 할 때 게임 세계에 관해 생각해볼 수 있는 간단한 항법은 윈도우의 해상도를 떠올리는 것이다. 예를 들어 게임 창이 $1024\times 768$ 이라면 일반적오 게임 세계를 해당 해상도보다 더 크게 만들지는 않는다. 다시 말해 창의 중심이 세계 공간의 원점이고 세계 공간에서의 단위와 창의 화면 픽셀이 1:1 비율인 세계 공간의 시점을 고려해보자. 이 경우에는 세계 공간에서 1단위를 위로 이동하면 창에서 1픽셀 위로 아동시키는 것과 같다. 이런 세계 시점에서 세계 공간을 클립 공간으로 변환하는 것은 어렵지 않다. 단순히 x좌표를 너비/2로 나누고 y좌표를 높이/2로 나누면 된다. 2D 동차좌표 행렬 형태인 뷰-투영 행렬은 다음과 같다.

$SimpleViewProjection=\begin{bmatrix}2/whidth&0&0\\0&2/heigth&0\\0&0&1\\ \end{bmatrix}$

예를 들어 $1024\times 768$ 해상도의 점 (256, 192)가 세계 공간에 주어졌을때 점을 SimpleVoewProjection으로 곱하면 다음과 같은 결과를 얻을 수 있다

$\begin{bmatrix}256&192&1\\ \end{bmatrix}\begin{bmatrix}2/1024&0&0\\0&2/768&0\\0&0&1\\ \end{bmatrix}=\begin{bmatrix}512/1024&384/768&1\\ \end{bmatrix}=\begin{bmatrix}0.5&0.5&1\\ \end{bmatrix}$

이 식이 잘 동작하는 이유는 정규화된 장치 좌표처럼 x축 [-512, 512] 범위를 [-1, 1]로 정규화했고, y축의 [-384, 384] 범위를 [-1, 1]로 정규화했기 때문이다. 이제 세계 변환 행렬과 SimpleViewProjection 행렬을 결합하면 오브젝트 공간의 임의의 버텍스 x를 다음과 같이 클립 공간으로 변환하는 것이 가능하다.

$v^{'}=v(WorldTransform)(SimpleViewProjection)$

위 식은 모든 버텍스에 대해 SimpleViewProjection이 그 유용성을 지속하는 한 버텍스 셰이더에서 계속 사용한다.

변환 행렬을 사용하는 셰이더로 갱신

변환 행렬을 사용하는 셰이더로 갱신하기 위해 Transform.vert라는 새로운 버텍스 셰이더 파일을 만들 것이다. 먼저 타입 지정자 uniform으로 Transform.vert 파일 내에 새로운 전역 변수를 선언한다. uniform은 셰이더 프로그램의 수많으 호출 사이에서도 동일하게 유지되는 전역변수이다. 이 변수는 셰이더가 실행될 때마다 매번 변경되는 in, out 변수와는 대조가 된다. uniform 변수를 선언하려면 uniform 키워드를 타입, 이름 앞에 놓는다. 이번 예에서는 2개의 다른 행렬이 필요하다. 다음과 같이 이 2개의 uniform 변수를 선언한다.

uniform mat4 uWorldTransform;
uniform mat4 uViewProj;

여기서 mat4 타입은 3D 공간에서 동차 좌표가 필요한 $4\times 4$ 행렬에 해당한다. 그리고 버텍스 셰이더의 메인 함수에서 코드를 변경한다. 먼저 3D inPosition을 동차 좌표로 변경한다.

vec4 pos = vec4(inPostion, 1.0);

이 위치는 오브젝트 공간에 있다, 그래서 이 다음에는 이 위치를 세계 변환 행렬로 곱해서 세계 공간 좌표로 변환해야한다. 그리고 변환된 위치값을 뷰-투영 행렬로 곱해서 클립 공간의 좌표로 변환한다.

gl_Position = pos * uWorldTransform* uViewProj;

Transform.vert

다음으로 Game::LoadShaders의 코드를 Basic.vert에서 Transform.vert를 사용하도록 변경한다. 이제 버텍스 셰이더는 세계 변환 행렬과 뷰-투영 행렬을 위한 uniform 변수가 필요하므로 이 uniform을 C++ 코드로 설정하는 방법이 필요하다. OpenGL은 활성화된 셰이더 프로그램에 uniform 변수를 설정하는 함수를 제공한다. 이런 함수의 래퍼(wrapper)함수는 Shader 클래스에 추가한다.

Shader::SetMatrixUniform

SetMatrixUniform 함수는 행렬뿐만 아니라 문자열로써 이름을 인자로 받는다. 이름은 셰이더 파일에서 변수 이름에 해당한다. 그래서 uWorldTransform에 대해서는 파라미터가 "uWorldTransform"이다. 두 번째 파라미터는 셰이더 프로그램의 해당 uniform을 보내는 행렬이다. SetMatrixUniform의 구현에서 glGetUniformLocation 함수 호출로 uniform의 위치 ID를 얻는다. 기술적으로 ID는 프로그램 실행동안 변경되지 않으므로 uniform을 업데이트 할때마다 ID값을 질의할 필요는 없다. 특정 uniform 값을 캐싱해두면 이 코드의 성능을 향상시킬 수 있다. glUniformMatrix4fv 함수는 행렬을 uniform에 할당한다. 이 함수의 세 번째 파라미터는 행 벡터를 사용한다면 GL_TRUE로 설정해야한다. GetAsFloatPtr 함수는 Matrix4의 간단한 헬퍼 함수로 행렬의 float*형 포인터이다. 이제 버텍스 셰이더의 행렬 uniform을 설정하는 방법을 알았으니 버텍스 셰이더에 행렬 uniform을 전달한다.이번 뷰-투영 행렬은 프로그램에사 변경되지 않으므로 뷰-투영 행랼은 한 번만 설정하면 충분하다. 그러나 화면에 그려지는 각 스프라이트 컴포넌트는 컴포넌트 소유자 액터의 세계 변환 행렬로 그려지므로 세계 변환 행렬은 프레임마다 설정해야한다. Game::LoadShaders에서는 화면 크기를 $1024\times 768$ 로 가정한 뷰-투영 행렬을 생성하고 난 다음, 이 행렬을 버텍스 셰이더에 전달하는 다음 두 라인을 추가한다.

SpriteComponent의 세계 변환 행렬은 약간 더 복잡하다. 액터의 세계 변환 행렬은 약간 더 복잡하다. 액터의 세계 변환 행렬은 게임 세계 에서 액터의 위치와 스케일, 그리고 방향을 나타낸다. 그러나 스프라이트의 경우에는 텍스처의 크기를 토대로 사각형의 크기를 스케일해야한다. 예를 들어 액터가 1.0f의 스케일을 갖고 있고 액터의 스프라이트에 해당하는 텍스처 이미지가 $128\times 128$ 이라면 단위 사각형을 그만큼 스케일 업해야한다.

먼저 텍스처의 너비와 높이로 스케일하기 위한 스케일 행렬을 생성한다. 그런다음 이 행렬을 소유자 액터의 세계 변환 행렬을 곱해서 스프라이트의 세계 변환 행렬을 완성한다. 다음으로 SetMatrixUniform을 호출해서 버텍스 셰이더 프로그램에 uWorldTransform을 전달한다. 마지막으로 glDrawElemet를 통해 삼각형을 그린다.