그래프의 표현
그래프는 노드(데이터를 표현하는 단위)와 에지(노드를 연결하는 선)로 구성된 집합이다. 그래프를 구현하는 방법은 크게 세 가지가 존재한다.
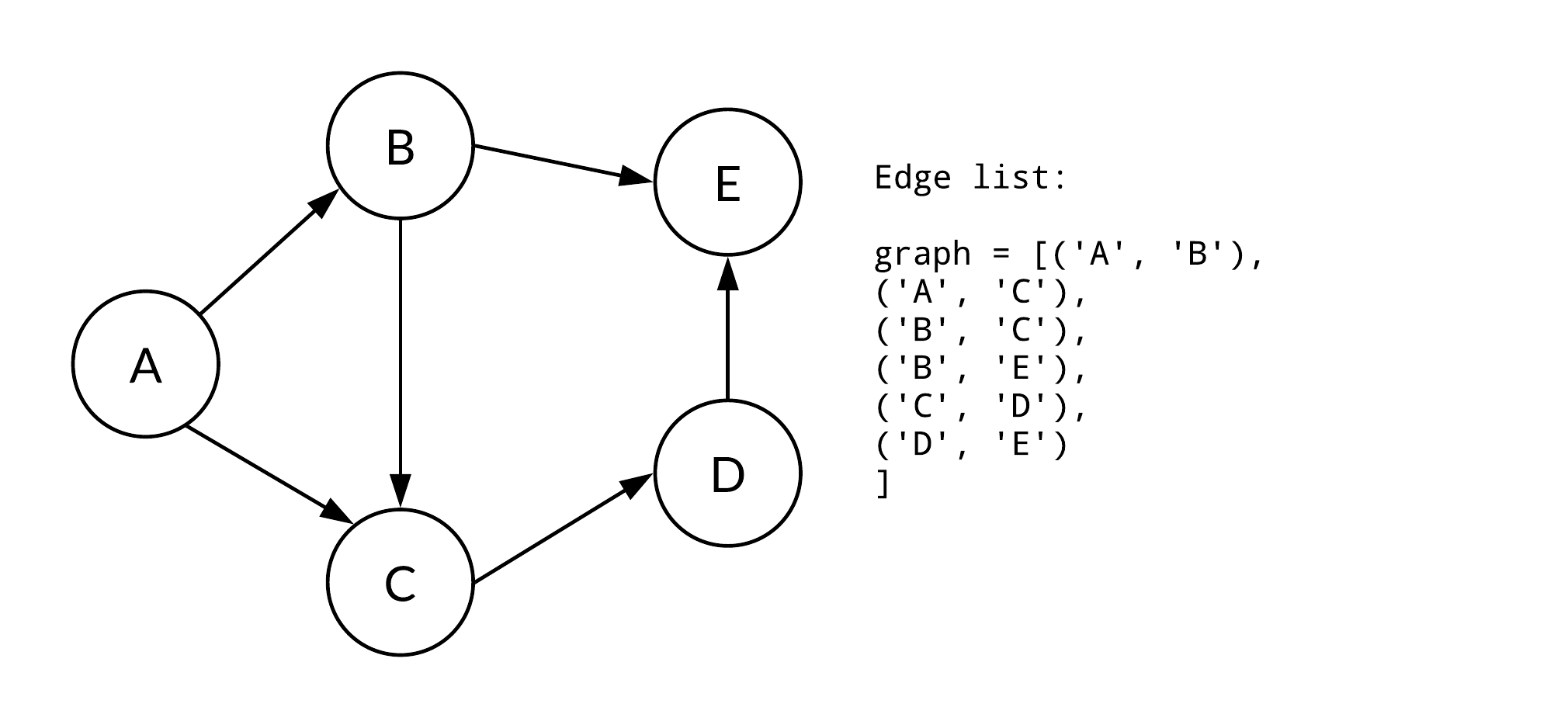
1. 에지 리스트
에지를 중심으로 그래프를 표현하는 방법이다. 배열에 출발 노드, 도착 노드를 저장하여 에지를 표현하거나 출발 노드, 도착 노드, 가중치를 저장하여 가중치가 있는 에지를 표현한다.
가중치가 없는 그래프
가중치가 없는 그래프는 출발 노드와 도착 노드만 표현하기 때문에 배열의 행은 2개면 충분하다. 노드는 여러 자료형을 사용할 수 있다.
가중치가 있는 그래프
가중치가 있는 그래프는 행을 3개로 늘려 3번째 행에 가중치를 저장한다.
에지 리스트는 구현하기 쉽지만 특정 노드와 관련되어 있는 에지를 탐색하기 쉽지 않다. 에지 리스트는 벨만-포드나 크루스칼 알고리즘에 사용되며, 노드 중심 알고리즘에는 잘 사용하지 않는다.
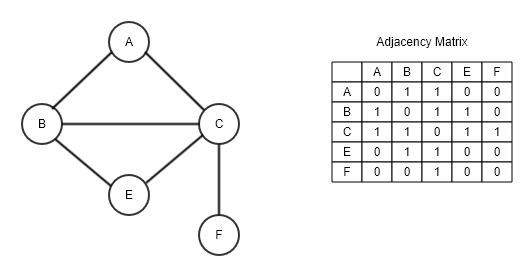
2. 인접 행렬
인접 행렬은 2차원 배열을 자료구조로 이용하여 그래프를 표현한다. 에지 리스트와는 다르게 노드 중심으로 그래프를 표현한다.
가중치가 없는 그래프
아래 그림과 같이 에지를 A행 B열에 1을 저장하는 방식으로 표현한다. 1을 저장하는 이유는 가중치가 없기 때문이다.
가중치가 있는 그래프
가중치가 있는 그래프는 앞의 가중치가 없는 그래프에서 에지의 위치에 가중치를 기록한다.
인접 행렬의 구현은 쉽고, 두 노드를 연결하는 에지의 여부와 가중치 값을 배열에 직접 접근하여 바로 확인할 수 있다는 장점이 있다.
그러나 노드와 관련되어 있는 에지를 탐색하기 위해서 N번 접근해야 하며, 노드 개수에 비해 에지가 적을 때 공간 효율성이 떨어진다. 또한 노드 개수가 많은 겨우 2차원 배열 선언 자체를 할 수 없는 결함도 있다.(노드 개수가 3만개가 넘을 경우 Java 힙 스페이스 에러 발생)
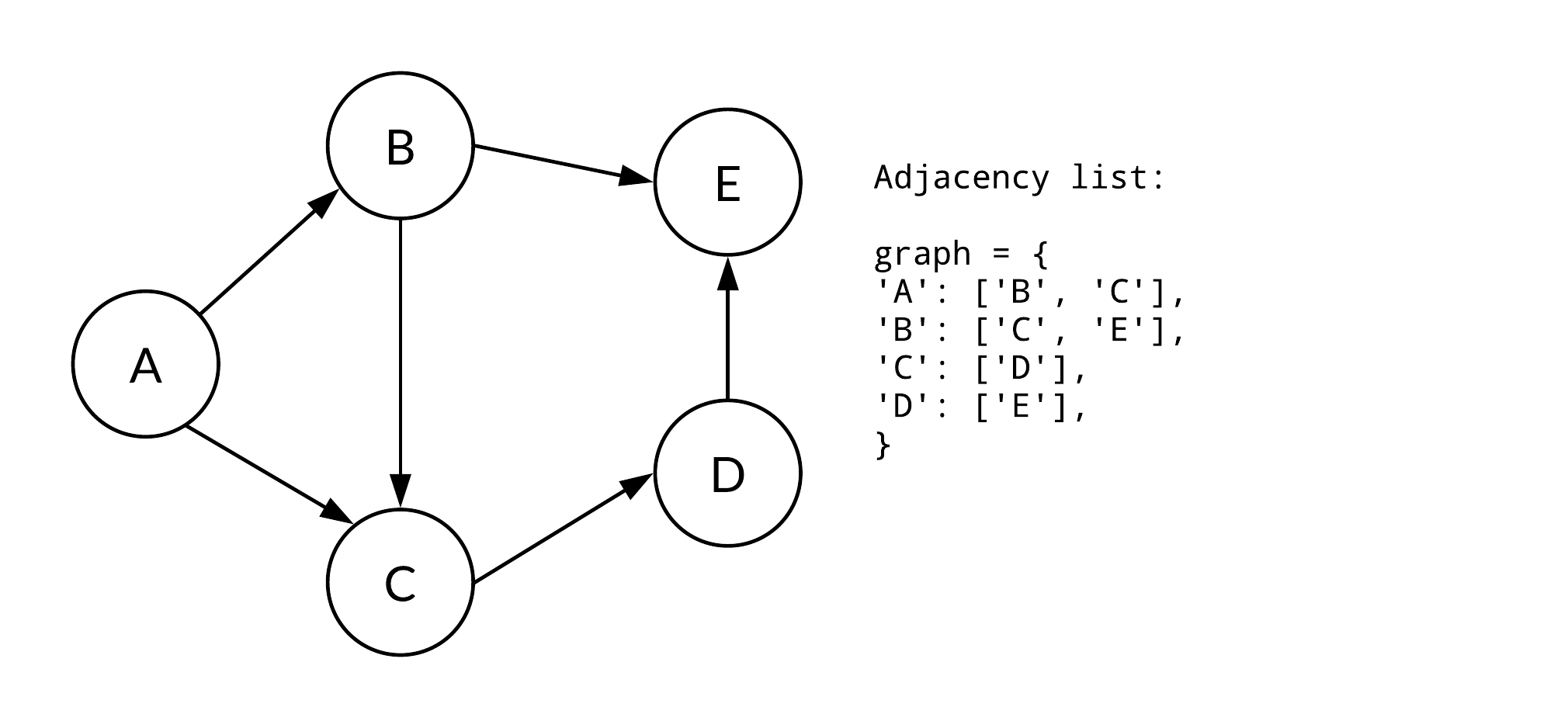
3. 인접 리스트
인접 리스트는 ArrayList로 그래프를 표현한다. 노드 개수만큼 ArrayList를 선언하고, 알맞는 자료형을 사용한다.
가중치가 없는 그래프
인접 리스트에는 N번 노드와 연결되어 있는 노드를 배열의 위치 N에 연결된 노드 개수만큼 배열을 연결하는 방식으로 표현한다.
가중치가 있는 그래프
가중치가 있는 경우 자료형을 클래스로 사용한다. Node 클래스를 선언하여 ArrayList에 사용한다.
다른 방법들에 비해 인접 리스트를 이용한 그래프 구현은 복잡한 편이지만, 노드와 연결되어 있는 에지를 탐색하는 시간이 매우 뛰어나며, 노드 개수가 커도 공간 효율이 좋아 메모리 초과 에러도 발생하지 않는다.
그래프 표현 구현
import java.util.*;
import java.io.*;
class Main {
static ArrayList<Integer>[] A ; // 그래프 데이터 저장 인접 리스트
static int[] check; // 이분 그래프 체크 배열
static boolean[] visited; // 방문 기록 저장 배열
static boolean isEven; // 이분 그래프 여부
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int testCase = Integer.parseInt(br.readLine());
for (int t = 0; t < testCase; t++) {
String[] s = br.readLine().split(" ");
int v = Integer.parseInt(s[0]); // 노드 개수
int e = Integer.parseInt(s[1]); // 에지 개수
A = new ArrayList[v + 1]; // 노드는 무조건 1번 부터 시작
visited = new boolean[v + 1];
check = new int[v + 1];
isEven = true;
for (int i = 1; i <= v; i++) {
A[i] = new ArrayList<Integer>();
}
// 에지 데이터 저장
for (int i = 0; i < e; i++) {
s = br.readLine().split(" ");
int start = Integer.parseInt(s[0]);
int end = Integer.parseInt(s[1]);
A[start].add(end);
A[end].add(start);
}
// 모든 노드에서 DFS 실행
for (int i = 1; i <= v; i++) {
if (isEven) {
DFS(i);
} else {
break;
}
}
if (isEven) System.out.println("YES");
else System.out.println("NO");
}
}
public static void DFS(int start) {
visited[start] = true;
for (int i : A[start]) { // 인접 리스트로 받아서 start에서 연결된 모든 노드 탐색
if (!visited[i]) {
check[i] = (check[start] + 1) % 2;
DFS(i);
} else {
if (check[start] == check[i]) {
isEven = false;
}
}
}
}
}유니온 파인드
그래프에서의 유니온 파인드는 그래프의 사이클이 생성되는지 판별하는 알고리즘이다.
위상 정렬
사이클이 없고, 방향이 있는 그래프를 정렬하는 알고리즘으로 그 결과가 한 개 이상일 수 있다.
다익스트라
최단거리 알고리즘으로, 시작점이 있고 다른 모든 노드로 가는 최단거리를 구하는 알고리즘이다. 단, 음수간선이 존재하면 안된다.
벨만-포드
최단거리 알고리즘으로, 시작점이 있고 다른 모든 노드로 가는 최단거리를 구하는 알고리즘이다. 음수간선이 존재해도 구할 수 있다. 음수 사이클이 존재하는지 체크하는데 많이 사용된다.
노드 수를 V, 에지 수를 E라고 했을 때 O(VE)의 시간 복잡도를 갖는다.
핵심 이론
1. 에지 리스트로 그래프 구현 후 최단 경로 리스트 조회
벨만-포드 알고리즘은 에지를 중심으로 동작하기 때문에 그래프를 에지 리스트로 구현한다. 또한 최단 경로 리스트를 출발 노드는 0, 나머지 노드는 무한대(적당히 큰 수)로 초기화 한다.
2. 모든 에지를 확인하며 정답 리스트 업데이트
최단 거리 리스트에서 업데이트 반복 횟수는 노드 개수 -1이다.(이 이상일 경우 무조건 사이클이 생긴다.) 업데이트 반복 횟수가 K번이라면 해당 시점에 정답 리시트의 값은 시작점에서 K개의 에지를 사용했을 때 각 노드에 대한 최단 거리이다.
업데이트 조건과 방법
시작점의 값 != ∞이며, 도착점의 값 > 시작점의 값 + 가중치일 때 도착점의 값 = 시작점의 값 + 가중치로 리스트 값을 업데이트한다.
음수 사이클이 없을 때 N - 1번 에지 사용 횟수를 반복하면 출발 노드와 모든 노드 사이의 최단 거리를 구할 수 있다. 이렇게 완성된 정답 리스트를 통해 해당 그래프에 음수 사이클이 존재하는지 여부를 확인해야 한다.
3. 음수 사이클 유무 확인
음수 사이클 유무를 확인하기 위해 모든 에지를 한 번씩 다시 사용해 업데이트되는 노드가 발생하는지 확인한다. 업데이트되는 노드가 있다면 음수 사이클이 존재한다는 의미이며, 최단 거리를 찾을 수 없는 그래프라는 뜻이 된다.(음수 사이클이 존재할 경우 무한하게 돌며 가중치가 감소하므로 구할 수 없다.)
플로이드-워셜
시작점이 존재하지 않고, 어느 노드에서 시작해도 최단거리를 구할 수 있는 알고리즘으로, 음수 가중치 에지가 있어도 수행할 수 있지만 음수 사이클이 존재하면 안된다. 단 시간복잡도가 좋지 않다.(O(노드의 수³))
핵심 이론
플로이드-워셜의 핵심 원리는 A 노드에서 B 노드까지 최단 경로를 구했다고 가정했을 때 최단 경로 위에 K 노드가 존재한다면 그것일 이루는 부분 경로 역시 최단 경로라는 것이다.
플로이드-워셜 점화식
D[S][E] = Math.min(D[S][E], D[S][K] + D[K][E])
1. 리스트 선언 후 초기화
D[S][E]는 노드 S에서 노드 E까지의 최단 거리를 저장하는 리스트라 정의한다. S와 E의 값이 같은 칸은 0, 다른 칸은 무한대로 초기화 한다. 여기서 S == E는 자기 자신에게 가는데 걸리는 최단 경로값을 의미하기 때문이다.
2. 최단 거리 리스트에 그래프 데이터 저장
출발 노드는 S, 도착 노드는 E, 가중치 W일 때 D[S][E] = W로 에지의 정보를 리스트에 입력한다.(인접 행렬)
3. 점화깃으로 리스트 업데이트
기존에 구했던 점화식을 3중 for문의 형태로 반복하면서 리스트의 값을 업데이트한다.
for 경유지 K에 관해 (1 ~ N)
for 출발 노드 S에 관해 (1 ~ N)
for 도착 노드 E에 관해 (1 ~ N)
D[S][E] = Math.min(D[S][E], D[S][K] + D[K][E])최소 신장 트리
그래프의 모든 노드를 연결하는데 사용된 에지들의 가중치의 합을 최소로 하는 트리이다. 크루스칼 알고리즘과 프림 알고리즘을 사용할 수 있다.
사이클이 포함되면 가중치의 합이 최소가 될 수 없기 때문에 사이클을 포함하지 않으며, N개의 노드가 있으면 최소 신장 트리를 구성하는 에지의 개수는 항상 N-1 개이다.
핵심 이론
1. 에지 리스트로 그래프를 구현한 후 유니온 파인드 리스트 초기화
최소 신장 트리는 데이터를 노드가 아닌 에지 중심으로 저장하기 때문에 인접 리스트가 아닌 에지 리스트로 저장한다. 일반적으로 노드 변수 2개와 가중치 변수로 구성되며, 사이클 처리를 위한 유니온 파인드 리스트도 함께 초기화 한다. 리스트의 인덱스는 해당 자리의 값으로 초기화한다.
2. 가중치 기준으로 그래프 정렬
에지 리스트에 담긴 그래프 데이터를 가중치 기준으로 오름차순 정렬한다.
3. 가중치가 낮은 에지부터 연결 시도
가중치가 낮은 에지부터 순서대로 연결을 시도하며 바로 연결하는 것이 아닌 이 에지를 연결했을 때 그래프에 사이클 형성 유무를 find 연산을 이용해 확인한 후 사이클이 형성되지 않을 때만 union연산을 이용해 두 노드를 연결한다.
4. 앞의 단계 3을 반복
전체 노드의 개수가 N개이면 연결한 에지의 개수가 N-1이 될 때까지 과정 3을 반복한다.
5. 총 에지 비용 출력
에지의 개수가 N-1이 되면 알고리즘을 종료하고, 완성된 최소 신장 트리의 총 에지 비용을 출력한다.
최소 신장 트리는 다른 그래프 알고리즘과 달리 에지 리스트의 형태를 이용해 데이터를 담는다. 또한 사이클이 존재하면 안되기 때문에 사이클 판별을 위한 유니온 파인드 알고리즘을 내부에 구현해야 한다.
