Understanding the Mel Spectrogram

다음 블로그를 번역했습니다.

Signals

signal은 시간이 지남에 따라 특정 양의 변화입니다. Audio의 경우 변화하는 양은 기압(air pressure)입니다. 이 정보를 디지털 방식(digitally)으로 캡처하려면 어떻게 해야 할까요? 시간이 지남에 따라 air pressure의 샘플을 얻을 수 있습니다. 데이터를 샘플링하는 속도는 다양할 수 있지만 가장 일반적으로 44.1kHz or 초당 44,100 samples 입니다. 이렇게 얻은 것은 신호에 대한 waveform이고, 아래처럼 컴퓨터로 해석, 수정 및 분석할 수 있습니다.

import librosa
import librosa.display
import matplotlib.pyplot as plt

y, sr = librosa.load('./example_data/blues.00000.wav')

plt.plot(y);
plt.title('Signal');
plt.xlabel('Time (samples)');
plt.ylabel('Amplitude');

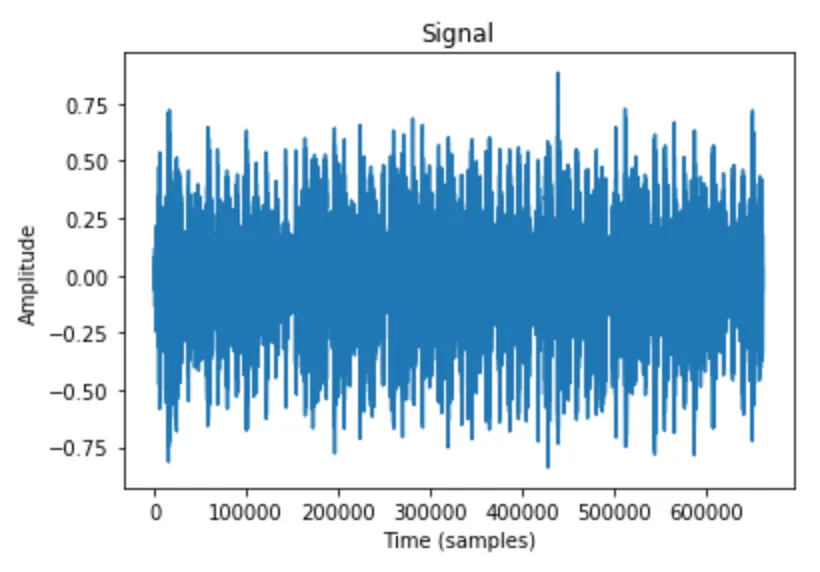
오오오 굿! 이렇게 다룰 수 있는 audio signal의 digital 표현을 얻을 수 있스빈다. Welcome to the field of signal processing!
근데 이렇게 마구잡이로 생긴것 같은데 어떻게 의미있는 정보를 얻을 수 있다는 거죠?Fourier!

The Fourier Transform

Audio signal은 여러 개의 single-frequency sound waves 로 구성됩니다. 시간 경과에 따라 signal의 sample을 수집할 때 result amplitudes만 얻을 수 있습니다.
Fourier Transform은 신호를 individual frequencies와 frequency’s amplitude 로 분해할 수 있는 수학 공식입니다. 즉, 시간 도메인의 신호를 주파수 도메인으로 변환합니다. 그 결과를 spectrum 이라고 합니다.

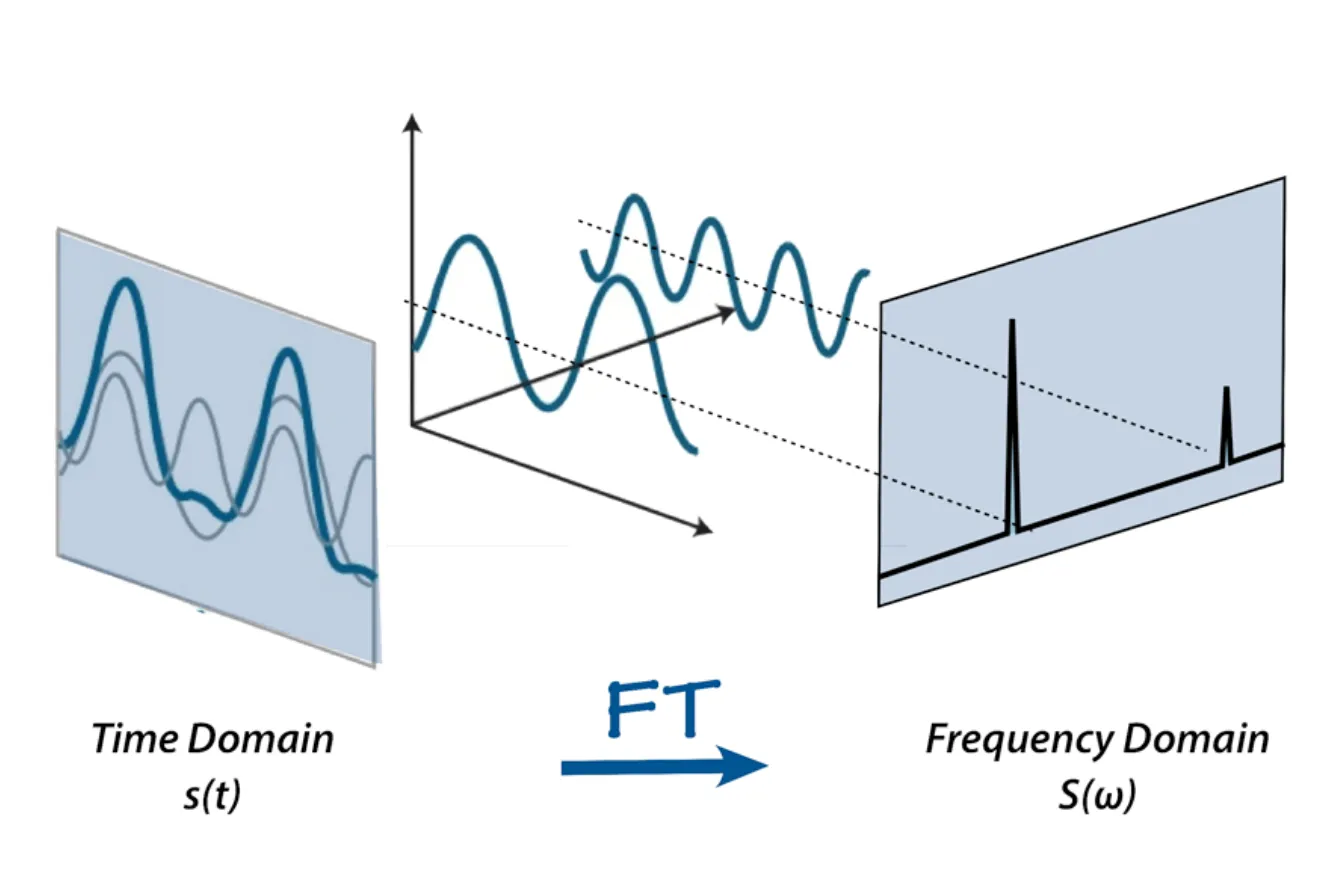
이게 가능한 이유는 원래 모든 signal이 original signal에 더해지는 일련의 sine waves와 cosine waves로 분해될 수 있기 때문입니다.→ Fourier’s theorem(phenomenal video)

Fast Fourier Transform(FFT) 은 Fourier Transform을 효율적으로 계산할 수 있는 알고리즘으로 Signal processing(신호 처리) 에 널리 사용됩니다. example audio의 windowed segment에서 이 알고리즘을 사용해보겠습니다.

import numpy as np

n_fft = 2048
ft = np.abs(librosa.stft(y[:n_fft], hop_length = n_fft+1))

plt.plot(ft);
plt.title('Spectrum');
plt.xlabel('Frequency Bin');
plt.ylabel('Amplitude');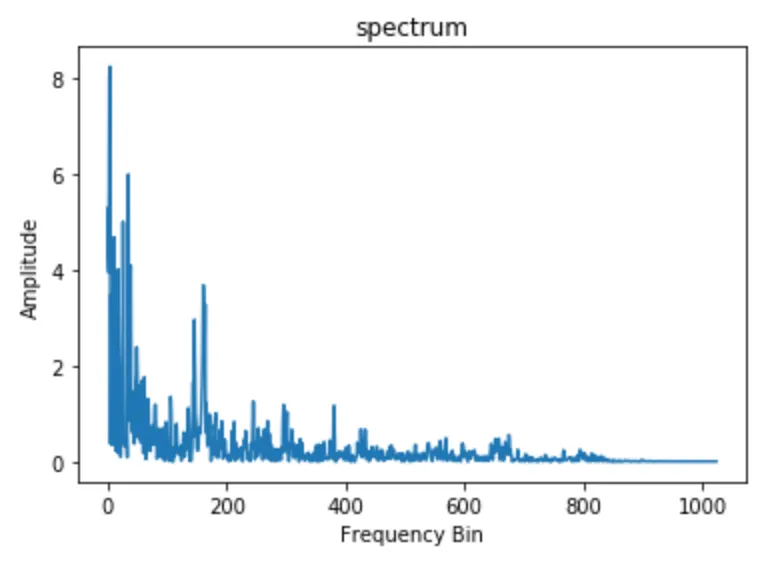

The Spectrogram

Fast Fourier Transform(FFT) 은 신호의 frequency content 를 분석할 수 있는 강력한 도구지만, 만약 이 신호의 frequency content가 시간에 따라 변하면 어떻게 될까요? (like music and speech)

이러한 신호를 non periodic(비주기적) 신호 라고 합니다. 이렇게 시간이 지남에 따라 달라지는 신호의 spectrum 을 나타내는 방법이 필요합니다.
"저기요, 신호의 여러 windowed segments 에서 FFT를 수행하여 여러 스펙트럼을 계산할 수는 없나여?"
Yes! 이것이 바로 필요한 작업이며 이를 short-time Fourier transform 이라고 합니다. FFT는 신호의 겹치는 windowed segments에서 계산되고, spectrogram 이라는 것을 얻습니다. WOW!

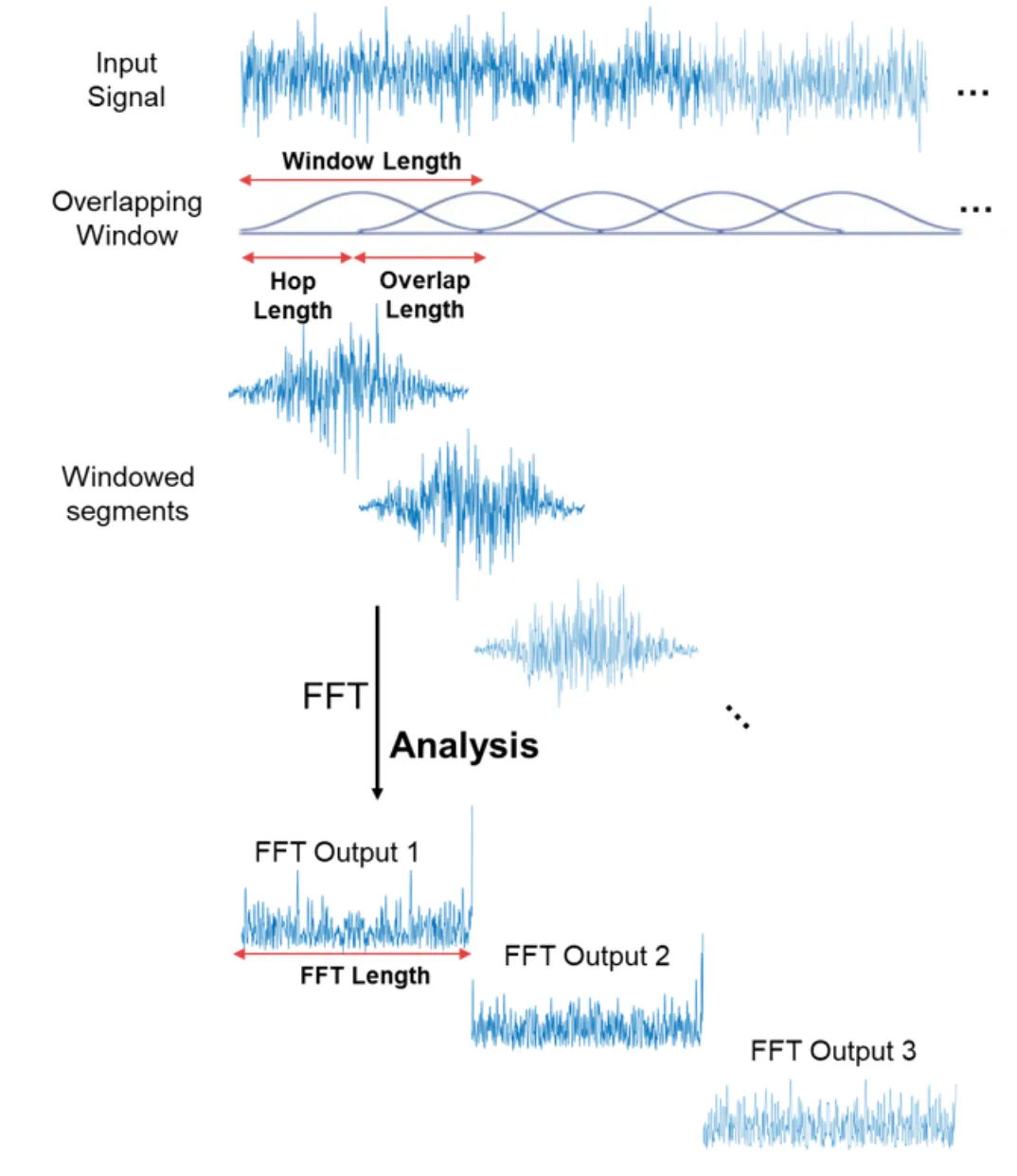
이제 spectrogram 은 FFT가 계속 쌓인 FFT 묶음으로 생각할 수 있습니다. 시간이 지남에 따라 서로 다른 주파수에서 달라지는 신호의 크기 또는 진폭을 시각적으로 나타내는 방법입니다. spectrogram을 계산할 때 추가적인 작업이 진행되는데, y축은 log scale로 변환되고 color dimension은 decibels로 변환됩니다. (log scale of the amplitude 로 생각할 수 있음). 이것은 인간이 매우 작고 집중된 범위의 주파수와 진폭만을 인지할 수 있기 때문입니다.

spec = np.abs(librosa.stft(y, hop_length=512))
spec = librosa.amplitude_to_db(spec, ref=np.max)
librosa.display.specshow(spec, sr=sr, x_axis='time', y_axis='log');
plt.colorbar(format='%+2.0f dB');
plt.title('Spectrogram');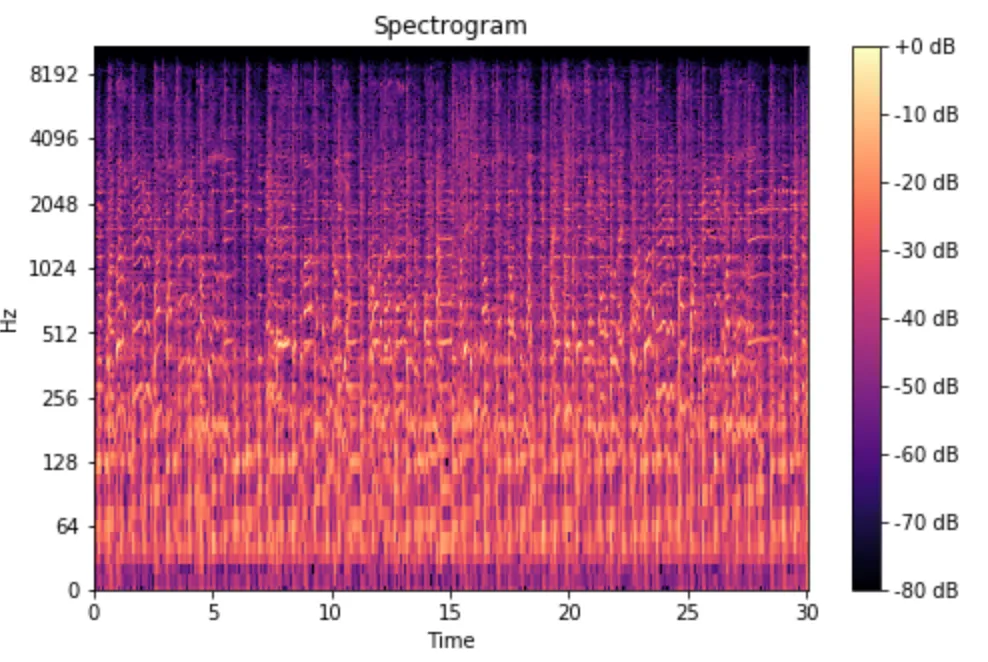

짜잔! 몇 줄의 코드만으로 spectrogram 을 만들었습니다. GOOD!.
그러면 이제 "Mel"은?

The Mel Scale

연구에 따르면 인간은 주파수를 linear scale (선형 척도) 로 인식하지 못합니다. 우리는 높은 주파수보다 낮은 주파수에서의 차이를 더 잘 감지합니다. 예를 들어 500Hz와 1000Hz의 차이는 쉽게 구분할 수 있지만 두 쌍 사이의 거리가 같더라도 10,000Hz와 10,500Hz의 차이는 거의 구분할 수 없습니다.

1937년에 Stevens, Volkmann, Newmann은 pitch 의 동일한 거리가 청취자에게 동일한 거리에서 들리도록 하는 pitch 단위를 제안했습니다. 이것을 mel scale 이라고 합니다. 주파수에 대한 수학적 연산을 수행하여 주파수를 mel scale 로 변환합니다.

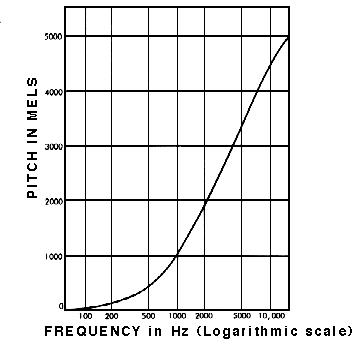
The Mel Spectrogram

Mel Spectrogram 은 주파수가 Mel Scale 로 변환되는 Spectrogram 입니다. WOW! 놀라운 점은 단 몇 줄의 코드로 구현할 수 있다는 것입니다.

mel_spect = librosa.feature.melspectrogram(y=y, sr=sr, n_fft=2048, hop_length=1024)
mel_spect = librosa.power_to_db(spect, ref=np.max)

librosa.display.specshow(mel_spect, y_axis='mel', fmax=8000, x_axis='time');
plt.title('Mel Spectrogram');
plt.colorbar(format='%+2.0f dB');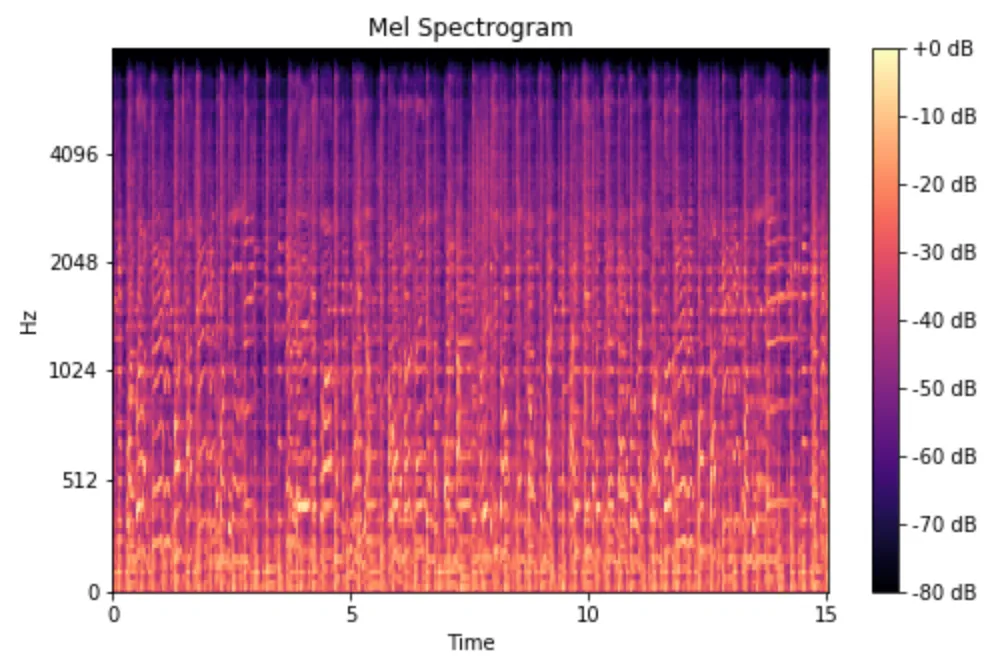

In Summary

1. 오디오 신호를 디지털 방식으로 표현하기 위해 시간 경과에 따른 air pressure 샘플을 얻었습니다.
2. 우리는 fast Fourier tranform을 사용해서 시간 영역에서 주파수 영역으로 오디오 신호를 매핑했고, 오디오 신호의 overlapping되는 windowed segments에서 이 작업을 수행했습니다.
3. Spectrogram 을 형성하기 위해 y축(주파수)을 로그 스케일로 변환하고 색상 차원(진폭)을 데시벨로 변환했습니다.
4. mel Spectrogram을 형성하기 위해 y축(주파수)을 mel 스케일에 매핑했습니다.