53. Minimum Distance Between BST Nodes

🎯 leetcode - 783. Minimum Distance Between BST Nodes

---

📌 문제

- 파이썬 알고리즘 인터뷰 53번 문제

📌 날짜

2020.02.22

📌 시도 횟수

5 try

💡 Code

class Solution:
    result = sys.maxsize
    prev = sys.maxsize

    def minDiffInBST(self, root: TreeNode) -> int:
        if not root:
            return 0
        if root.left:
            self.minDiffInBST(root.left)

        self.result = min(self.result, abs(self.prev - root.val))
        self.prev = root.val

        if root.right:
            self.minDiffInBST(root.right)

        return self.result

💡 문제 해결 방법

⭐ 중위 순회 ⭐

- 현재 노드를 기준으로 값의 차이가 가장 작은 노드를 찾으려면?
후보 1. 현재 노드 오른쪽 부분에서 가장 왼쪽에 있는 노드
후보 2. 현재 노드 왼쪽 부분에서 가장 오른쪽에 있는 노드
> 이걸 이해해야 풀 수 있었다!

- 그리고 이 순서대로 노드를 순회하는 탐색 방법이 바로 중회 순회이다.

- 이해가 안되면 아래 그림 참고!

추가 설명

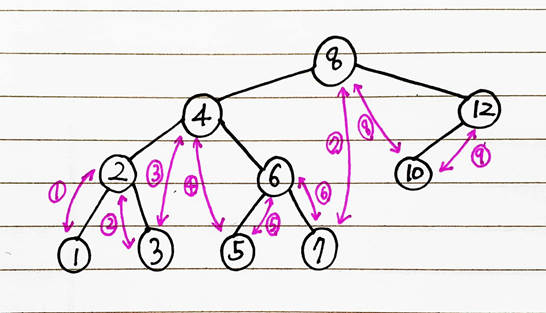
• 아래와 같은 이진 탐색 트리가 있다고 가정하자.
  

🥝 ex1 - 현재노드가 8이면 값의 차이가 가장 작은 노드가 될 수 있는 후보는,
1. 7 : 8의 왼쪽 부분에서 가장 오른쪽에 있는 값이다.
2. 10 : 8의 오른쪽 부분에서 가장 왼쪽에 있는 값이다.

🥝 ex2 - 현재노드가 4이면 값의 차이가 가장 작은 노드가 될 수 있는 후보는,
1. 3 : 4의 왼쪽 부분에서 가장 오른쪽에 있는 값이다.
2. 5 : 4의 오른쪽 부분에서 가장 왼쪽에 있는 값이다.

• 따라서 위의 개념을 바탕으로 값을 조사할 순서를 고려해보면 탐색 순서가중회 순회와 같음을 알 수 있다!
  

💡 새롭게 알게 된 점

- 기본적인 틀은 중회 순회로 구현하되, 이전에 탐색한 노드의 값과의 차이를 비교해야 
하므로 prev 값을 가져온 것!

❌ (한번에 맞추지 못한 경우) 오답의 원인

- 가장 작은 노드를 찾는 원리를 제대로 파악하지 못했다...

---

😉 다른 풀이

📌 하나. 위의 코드를 그대-로 반복문으로 구현

class Solution:
    def minDiffInBST(self, root: TreeNode) -> int:
        result = sys.maxsize
        prev = -sys.maxsize
        stack = []
        node = root
        while stack or node: 
            # ----- left -----
            while node:
                stack.append(node)
                node = node.left
                
            # ----- node -----
            node = stack.pop()
            result = min(result, node.val - prev)
            prev = node.val
			
            # ----- right -----
            node = node.right
        return result

💡 문제 해결 방법

- 오른쪽 자식 노드를 택하기 전에 비교하는 형태로 재귀와 동일하게 중위 순회로 풀이함
- 아래 그림을 보면 이해가 잘 된다.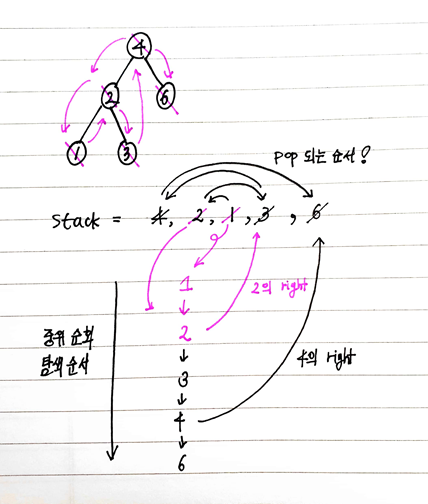

💡 새롭게 알게 된 점

- 재귀가 아닌 반복 구조로 중회 순회를 구현하는 방법을 알게 되었다.
- 이해하고 나니 반복 구조로 구현하는 게 더 직관적인 것 같다.

- 원래 반복구조 DFS는 항상 stack = [root]으로 시작했는데
이진탐색트리의 중회 순회에서는 stack을 빈 상태로 시작한다.
그리고 node라는 새로운 TreeNode를 추가하여 이 노드와 연결된 left를 우선적으로
stack안에 넣고, 더이상 left가 없을 때 right를 stack에 넣는다.

- 크게 보면 재귀와 구조가 비슷한 것 같다.
"중위 순회 : left -> node -> right" 라는 큰 틀에서 벗어나지는 않는 것 같다.