76. Minimum Window Substring

🎯 leetcode - 76. Minimum Window Substring

---

📌 문제

- 파이썬 알고리즘 인터뷰 76번 문제

📌 날짜

2020.03.06

📌 시도 횟수

4 try

💡 Code

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        need = collections.Counter(t)
        missing = len(t)
        left = start = end = 0
        
        # 오른쪽 포인터 이동
        for right, char in enumerate(s, 1):
            missing -= need[char] > 0
            need[char] -= 1
            
            # 필요 문자가 0이면 왼쪽 포인터 이동 판단
            if missing == 0:
                while left < right and need[s[left]] < 0:
                    need[s[left]] += 1
                    left += 1

		# 이전 결과보다 현재 경로의 길이가 더 작은 경우에만 start, end를 새롭게 갱신한다. 
                if not end or right - left <= end - start: 
                    start, end = left, right
                need[s[left]] += 1 # 다시 맨 앞의 값을 삭제하고 새롭게 찾는다.
                missing += 1 
                left += 1
        return s[start:end]

💡 문제 해결 방법

🥝 직접 보면 더 이해가 잘 된다

- 쉽게 생각하기 어려운 풀이이다.
- 아래 오답의 원인에서 말했듯, 이 문제는 O(n^2)이 아닌 O(n)으로 풀어야지
시간 내에 통과가 된다. 
- O(n)으로 풀기 위해, 투 포인터를 사용해야 했다!

✔ 풀이를 위한 전제 (이걸 이해하면 위의 코드가 좀 더 이해가 잘 된다)

📌 need[char]이 "양의 값"을 가지면 양의 값 만큼 해당 char이 "필요"하다는 의미이다.
> "ABBBEC" = {'C': 1, 'A': 0, 'E': -1, 'B': -2} 이다.
> {'C': 1, 'A': 0, 'E': -1, 'B': -2} : C가 1개 필요하고, A는 1개 있고, 
B는 (2 + 1) 3개 있고 E는 1개(t에 해당하는 값이 아니므로) 있다. 

📌 missing은 필요한 문자의 개수이다.
> 만약 현재 "ABBBAEDF"를 가지고 있다고 해도, t = "ABC" 중 "C"가 여전히 없는 
상태이므로 missing = 1이다.
> 이를 정상적으로 계산하기 위한 연산이 바로 아래 코드이다.
missing -= need[char] > 0
> 즉, 해당 char이 "필요한 값(need[char] > 0)"일 경우에만 missing을 1씩 감소시킨다.

✔ 방법

1. 일단 right가 left부터 차례대로 조사하면서 missing = 0이 될 때까지 이동한다.
2. missing = 0이 되면 현재 범위에서 가장 최소 길이의 문자열이 t("ABC")를 모두 가지고 있는 경우를 판별한다. 즉, left를 이번에는 오른쪽으로 이동하면서 t를 모두 포함하면서 문자열의 길이가 최소인 구역을 구한다.
3. start, end = left, right로 이전 결과의 인덱스를 저장해둔다.
   그리고 다시 새로운 left = left + 1에 대하여 1, 2의 과정을 반복한다.
   (맨 앞에서 뺀 s[left]를 다시 찾는 과정이 바로 1번 과정이다.)
4. 만약 2에서 새롭게 구한 left, right의 차이(문자열의 길이 right - left)가 이전 값(end - start)보다 큰 경우, 3번 과정에서 start, end를 새롭게 갱신하지 않는다.
   왜냐하면 우리가 구해야 될 값은 최소 길이 이기 때문이다!

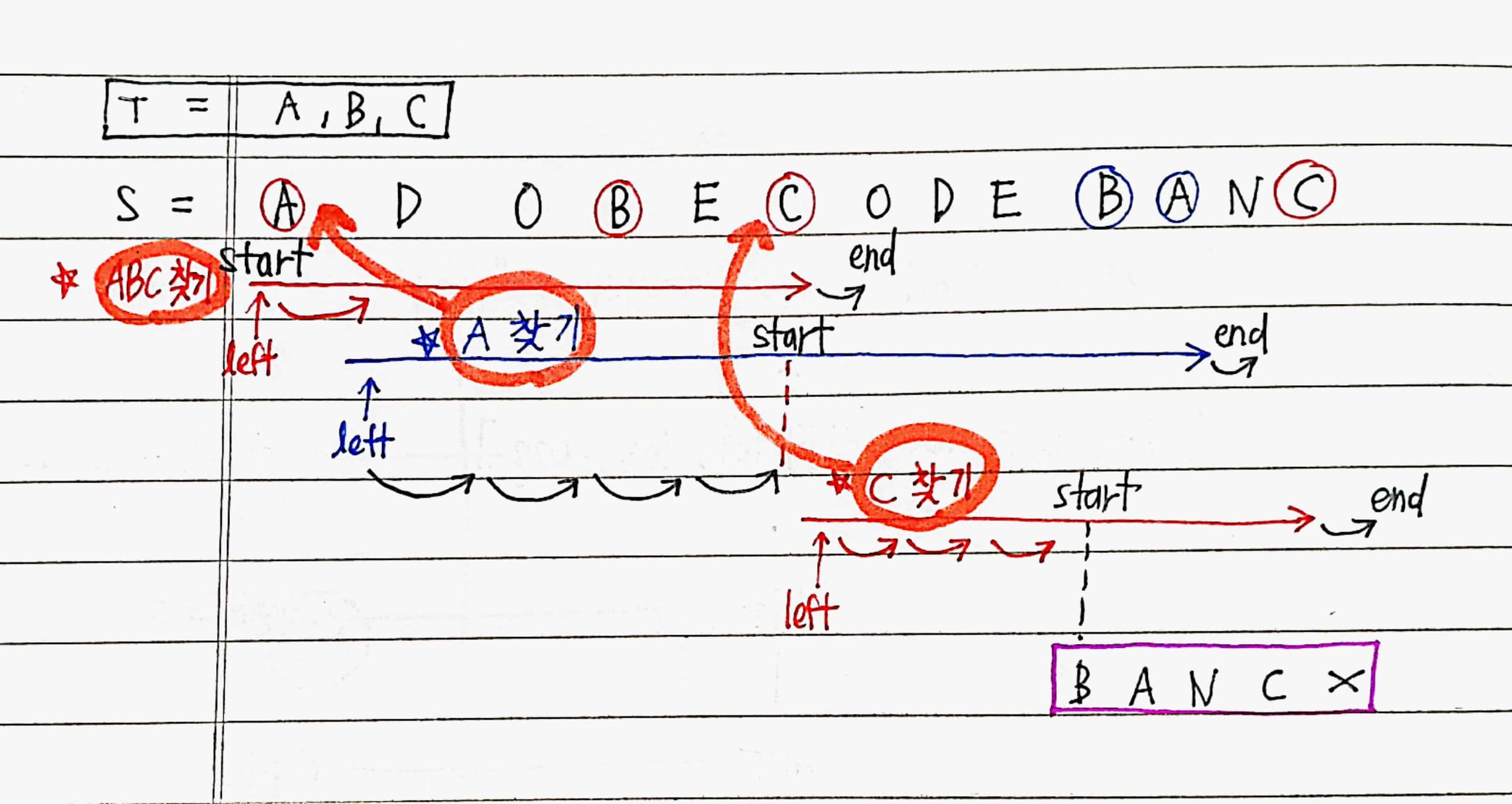
• 이제 아래 그림의 과정을 코드와 비교해보면서 이해해보자.
• 각 화살표는 missing == 0이 되는 시점을 기준으로 구분했다.
  

💡 새롭게 알게 된 점

- 어렵다ㅠㅠ
- 투 포인터를 사용하면 시간적인 면에서 정말 효율적이고 빠른 알고리즘을 구현할 수 있다!

❌ (한번에 맞추지 못한 경우) 오답의 원인

- O(n^2)에 풀었더니 타임 아웃으로 마지막 testcase가 통과하지 못했다.
- 타임 아웃이 뜬 코드는 아래와 같다. 나름대로 색다른 방법으로 빠르게 풀어보려고 
노력했는데 여전히 O(n^2)가 나왔다.

# 타임 아웃이 뜬 코드이다!!!
class Solution:
    def minWindow(self, s: str, t: str) -> str:
        def slidingWindow(left):
            new_set = tset
            new_set.remove(s[left])
            count = 0
            if not new_set:
                return 0

            for val in s[left + 1 :]:
                if val in new_set:
                    new_set.remove(val)
                count += 1
                if not new_set:
                    return count
            return float("inf")

        contain_list = []
        left = right = 0
        min_count = float("inf")
        result_left_idx = 0
        for i, a in enumerate(s):
            tset = list(t)
            if a in tset:
                re = slidingWindow(i)
                if re < min_count:
                    min_count = re
                    result_left_idx = i
        if min_count != float("inf"):
            return s[result_left_idx : result_left_idx + min_count + 1]
        return ""

---