🎯 [BOJ 17070번] 파이프 옮기기 1
🏆 문제 해결 방법
🔍차근차근 이해해봅시다
DP를 정~~말 어려워하는 제가 어떻게 이해했는지 적어보겠습니다!😆
- 먼저 가로, 세로, 대각선 파이프를 언제 놓을 수 있는지 분류해봅시다.
가로파이프는 이전에 설치한 파이프가가로,대각선일때 설치할 수 있죠.

세로파이프는 이전에 설치한 파이프가세로,대각선일때 설치할 수 있어요.

대각선파이프는 이전에 설치한 파이프가대각선,가로,세로모든 경우에서 설치 가능해요.

- 아! 근데 조건이 한가지 더 있죠? 바로
벽을 고려해주어야 하는데요
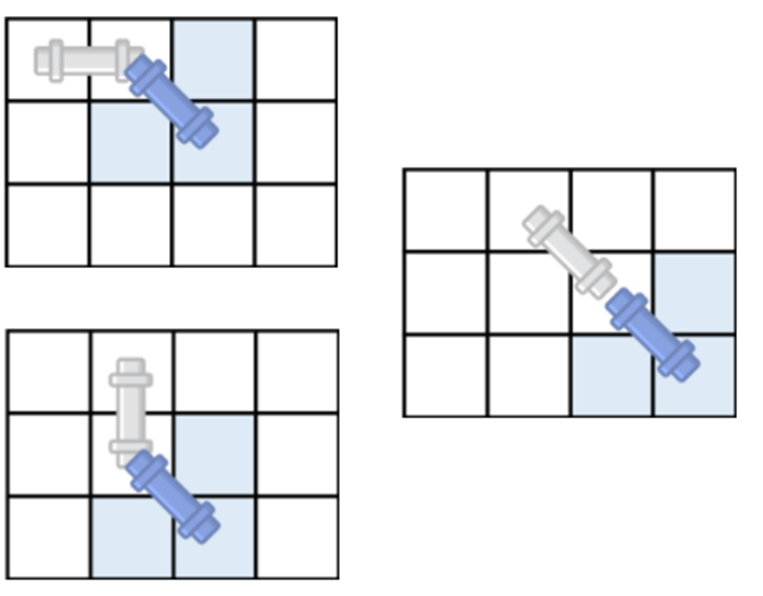
파이프를 새로 추가하려는 칸에벽이 없어야 하는건 당연한거니까,대각선파이프를 설치할때만 특별히 주의하시면 돼요~
대각선파이프를 설치하기 위해서는 아래 사진처럼 파이프를 새로 추가하려는 칸 뿐아니라왼쪽,위쪽또한 벽이 없어야 돼요! (즉, 아래 사진의 색칠된 칸 모양┘에 벽이 없어야 돼요) 여기까지는 어렵지 않게 이해하셨죠😉?
- 이제 위의 조건들을
dp라는 3차원 그래프에 담아보려고 해요! 우선 그림을 통해서 어떤식으로 담을지 보여드릴게요.
-
우선
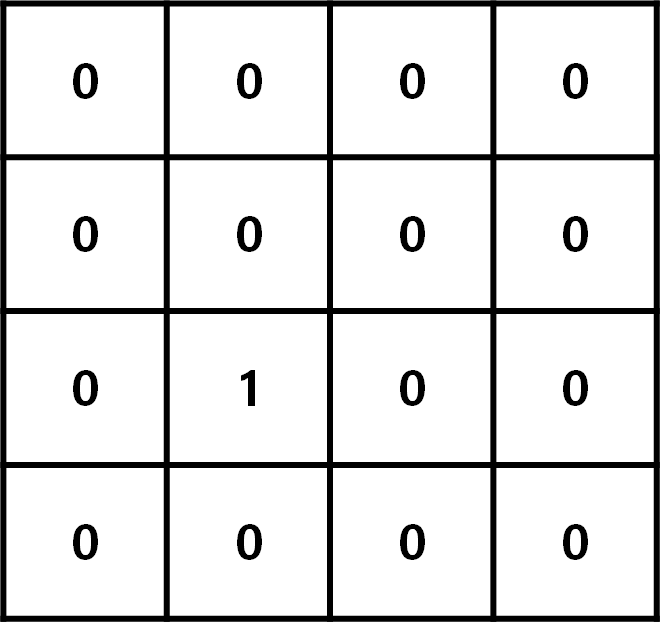
벽유무에 관한 (문제에서는 '집의 상태'라고 하더라고요?) 집 그래프를board라고 할게요.board는 그냥 input을 그대로 가져옵시다. (예시는 그냥 아무 예시나 가져와봤어요!)
-
이걸 바탕으로
dp의 초기 상태를 가져와보면 다음과 같아요.
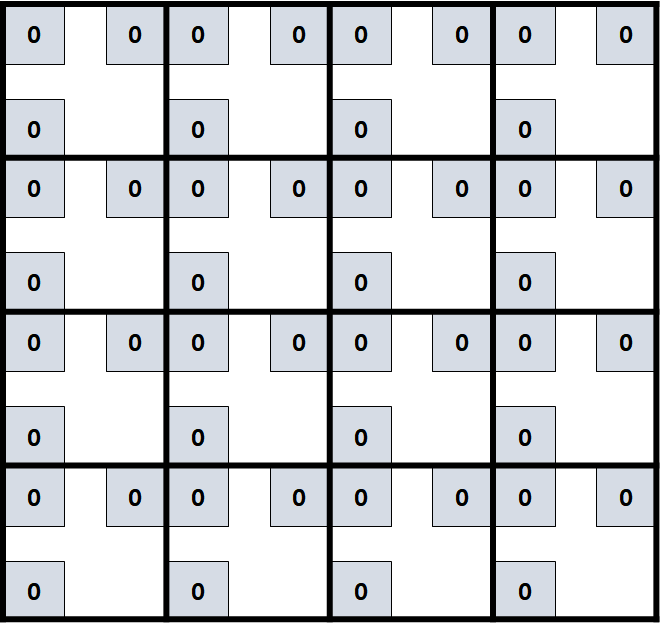
- 이게 대체 뭘까요😨?! (약간 환공포증이 생길것 같기도 하네요ㅠ..ㅠ)
- 왜 이렇게 그렸는지 설명해드릴게요!
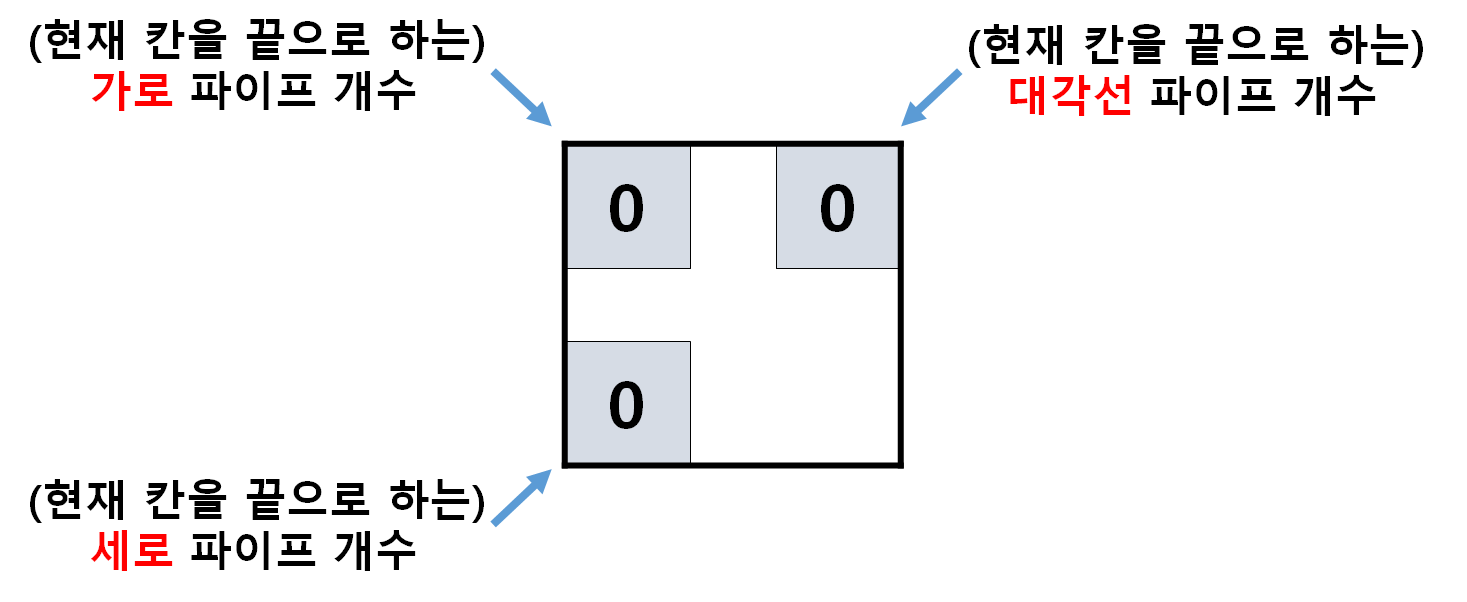
- 이해가 되시나요? 즉, 초기상태(가로 파이프 1개만 놓인 상태)를
dp로 표현해보면 아래와 같겠네요!
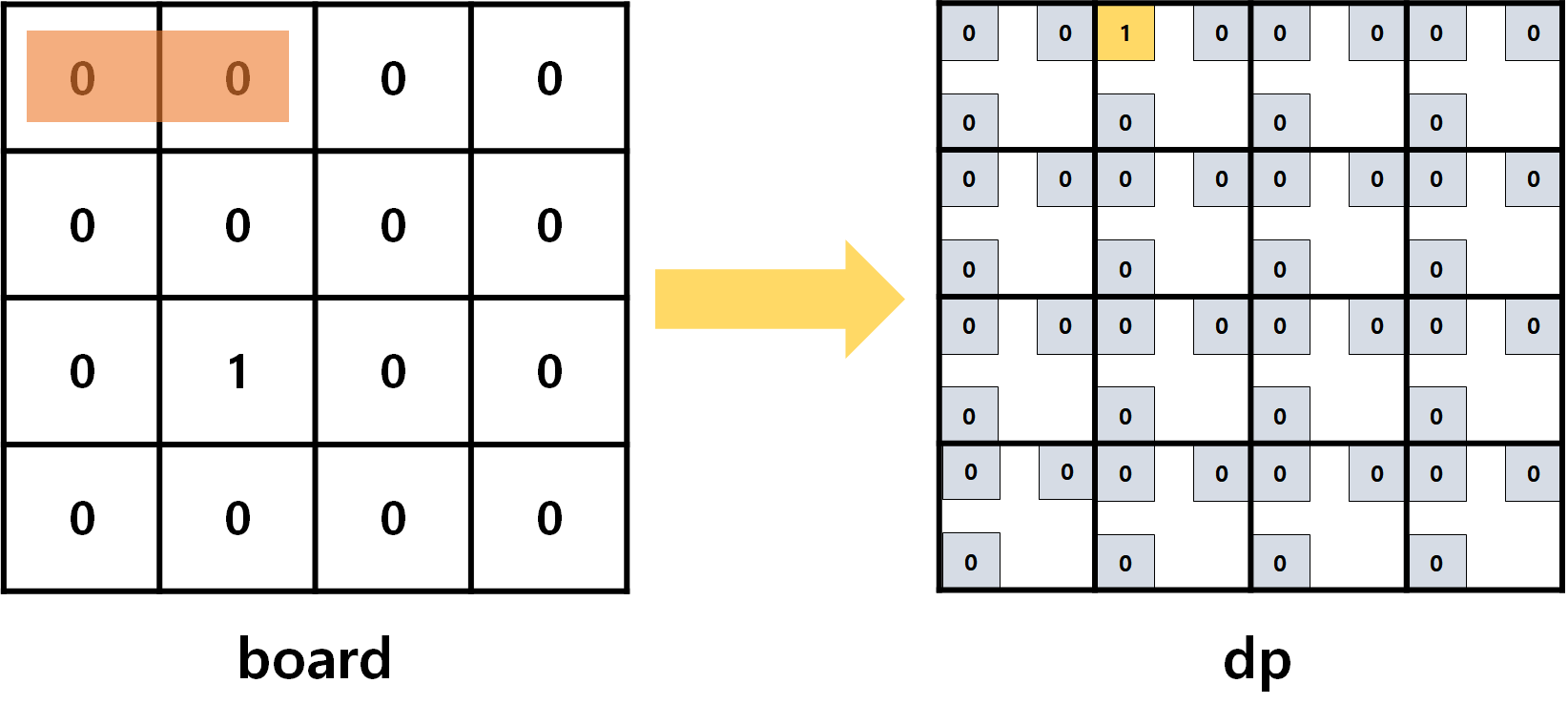
- 즉, dp에서 1이 된다는 것은, 해당 칸을 파이프의 끝으로 하는
가로또는세로또는대각선파이프가 1개 존재한다는 말이겠네요! 흠...이해되시나요😮?
- 여기까지 이해하셨으면 이제 본격적으로
dp로 풀어봅시다!
- 우선 미리 처리해주면 편한 것부터 처리를 해줍시다.
- 생각해보면 첫번째 행은 항상 가로 파이프만 올 수 있죠?
- 그림을 보면 쉽게 이해되실거예요.
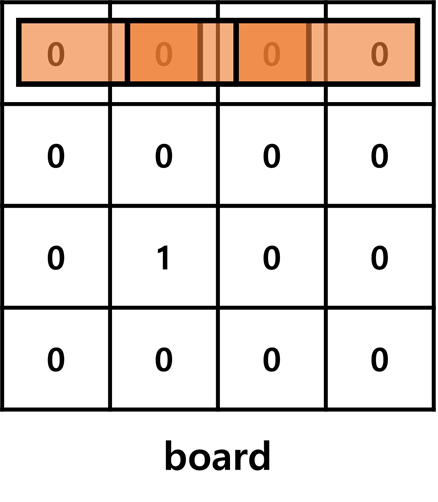
- 따라서 이건 미리
dp에 표시해줍시다.
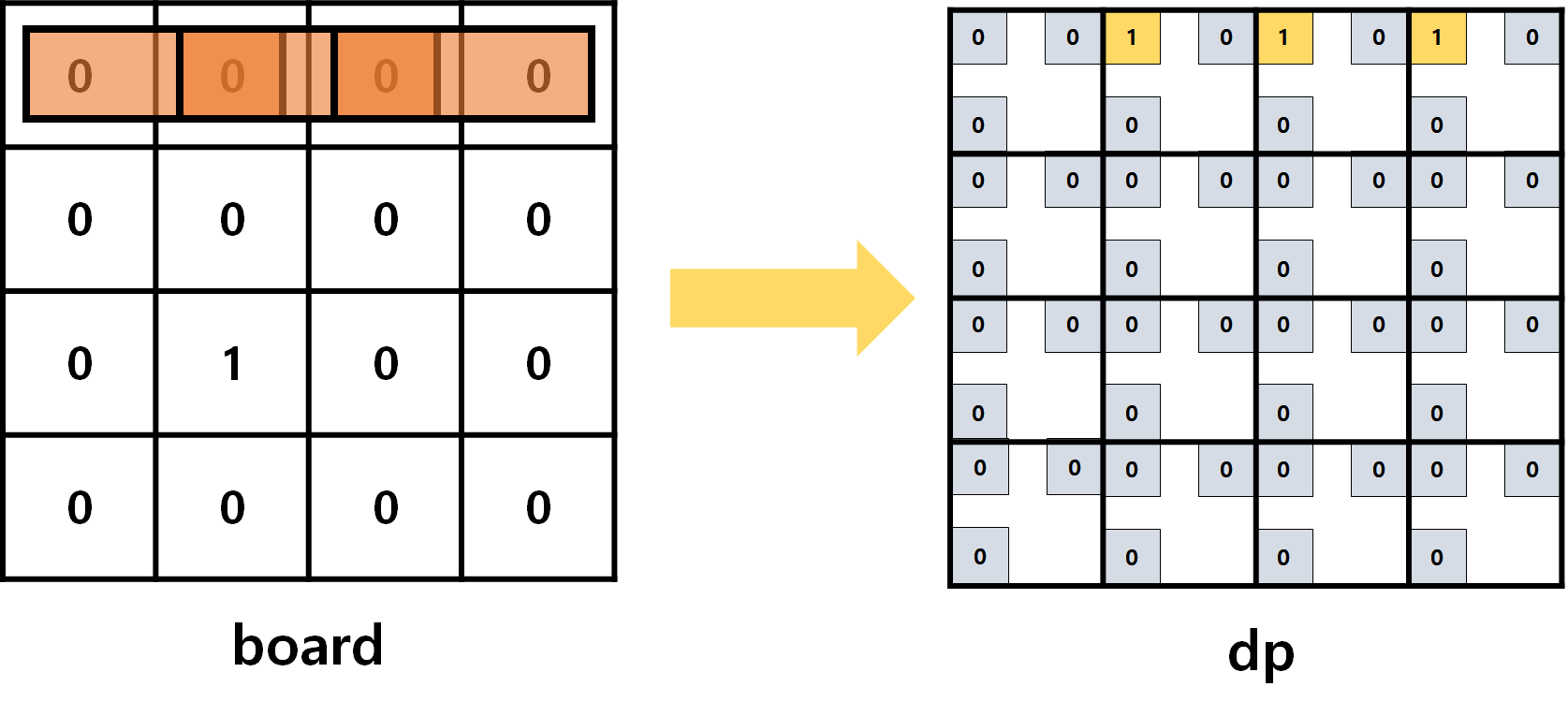
- 하나 더 생각해보면 과연 1열에 파이프의 끝이 오는 경우가 있을까요?
시작 파이프는 항상가로이기 때문에 1열에는 파이프의 끝이 오는 경우가 없다는 것을 금방 알아차릴 수 있을 거예요.
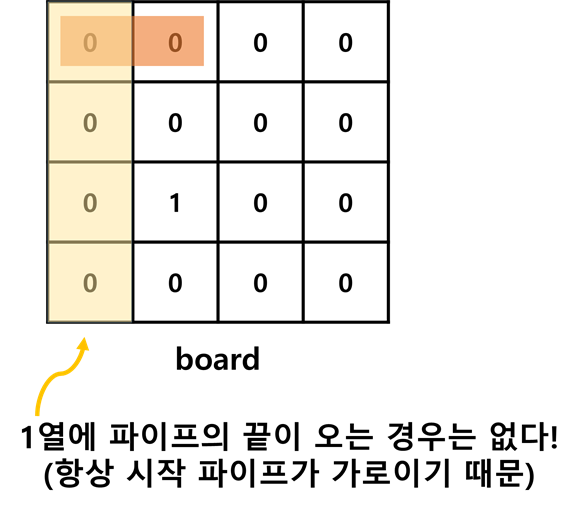
- 따라서 우리는
board[1][1]부터 처리해갈 거예요! 1행과 1열은 이미 3번, 4번 과정에서 다 처리를 해줬으니까~😉
- 처리 과정은 다음과 같아요!
- [1] 파이프를 설치할 공간이 있는지 확인하기!
→board에서벽이 있는지 없는지 검사해보고 (가로,세로,대각선) 파이프를 설치할 공간이 있는지 판단해요!
(위의 2번 과정에서 체크했던 조건을 검사해줄거예요) - [2] (파이프를 설치할 공간이 있다면) 이제 위의 1번 과정의 조건을 고려해줘야겠죠?
현재 칸에 파이프를 설치할 공간이 있다고 해도, 이전에 설치한 파이프가 어떤 것인지에 따라 놓지 못할 수도 있으니 이것도 고려를 해줘야해요! - [3] 최종적으로
dp에 결과를 저장해줍니다!
- [1] 파이프를 설치할 공간이 있는지 확인하기!
-
아직 이게 무슨말인지 살~짝 알듯말듯 하니까 다시 그림으로 차근차근 이해해봐요 :)
- 현재 우리가 검사하려고 하는 칸을 파란색으로 칠해봤어요.
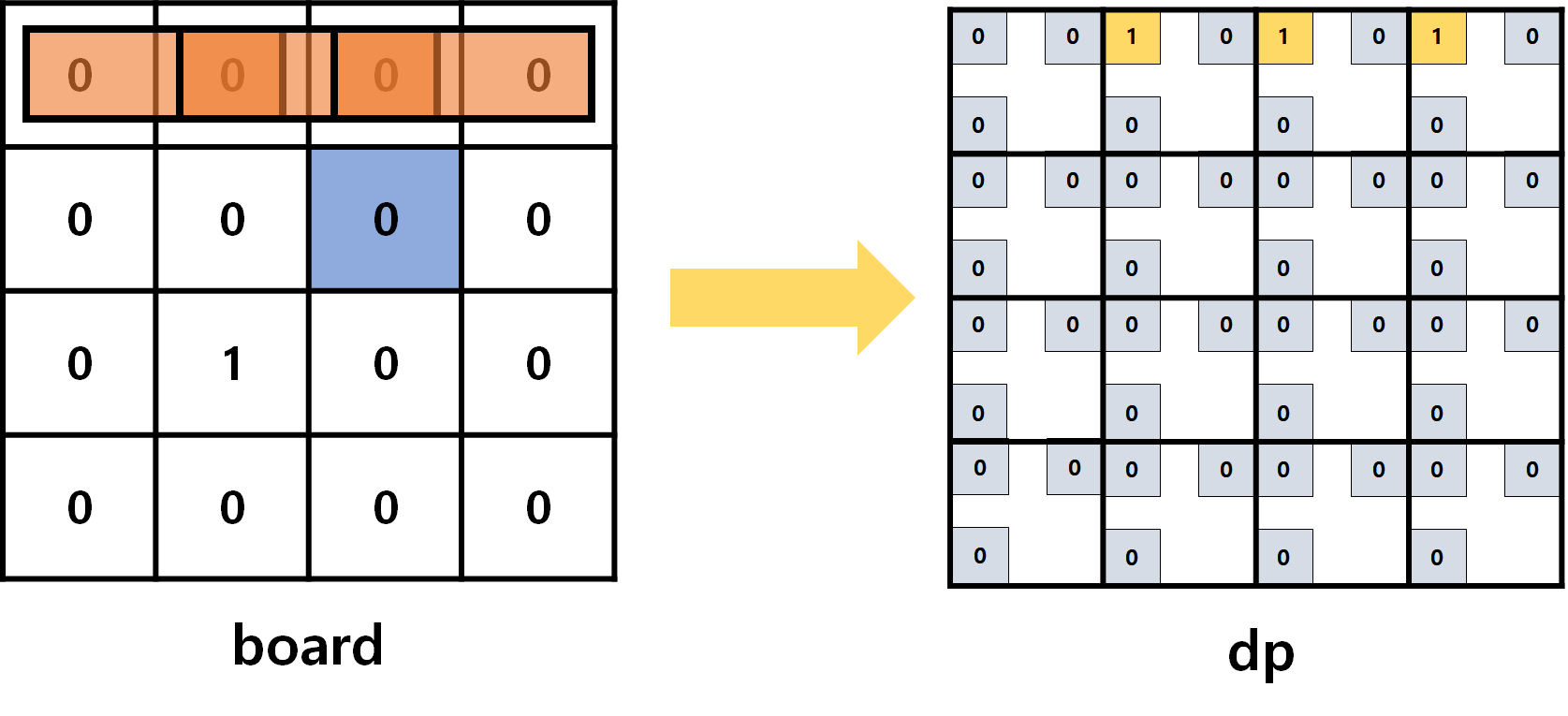
- 이게 살짝 헷갈릴수도 있는데.. 가장 중요한 것은!!
dp에 저장되는 값은 파이프의 끝의 개수를 가리킨다는 점이에요! - 아래 사진에서
dp를 왜 저렇게 표현했는지 완벽하게 이해하고 넘어가세요..!
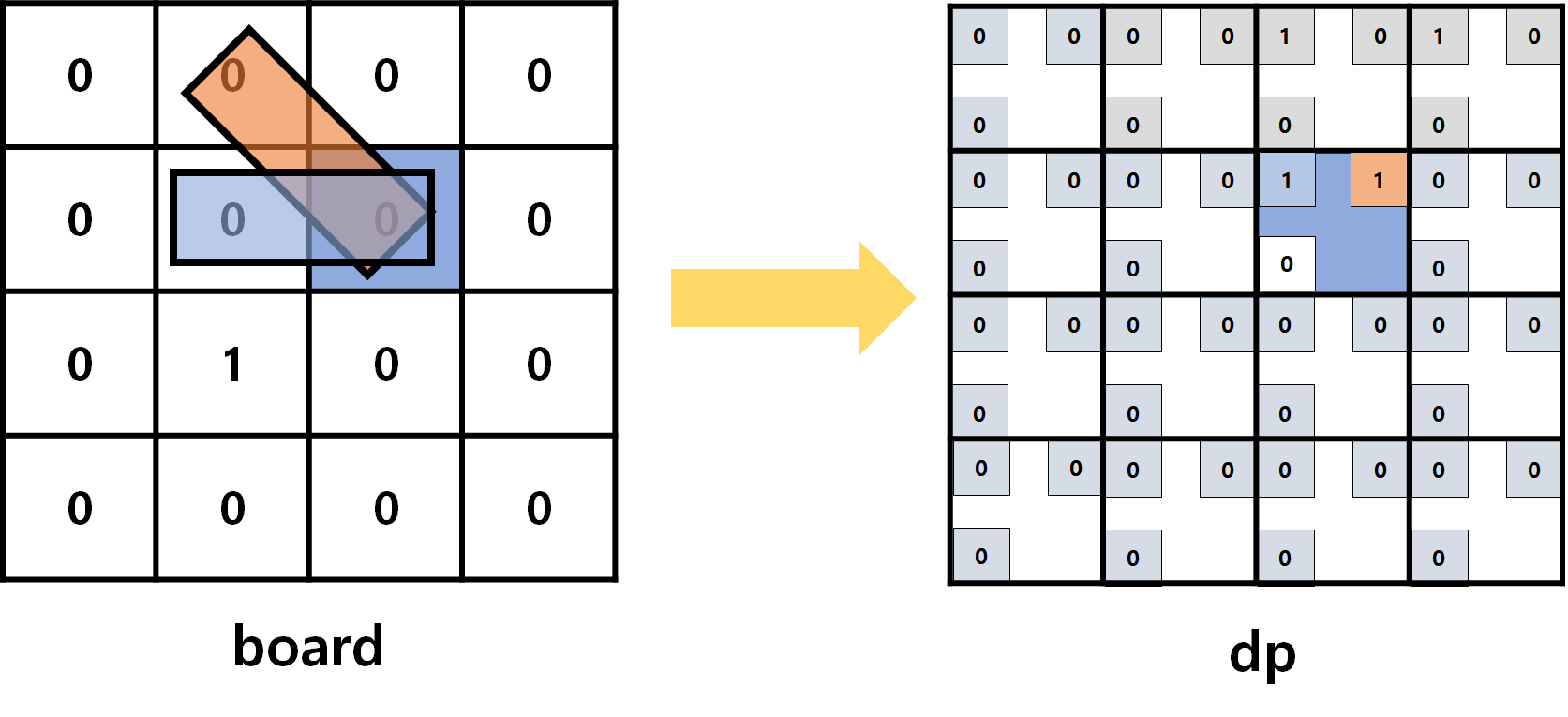
- 이게 살짝 헷갈릴수도 있는데.. 가장 중요한 것은!!
[1] 먼저 벽의 유무를 고려해봐요.
- 현재 칸은
0으로 벽이 없죠? →가로,세로파이프를 설치할 공간이 있어요. - 그리고 현재 칸의 위쪽, 왼쪽 칸도 모두
0이네요. →대각선파이프를 설치할 공간이 있어요. 가로,세로,대각선파이프 모두 설치할 공간이 충분히 있네요!
그럼 이제 [2] 조건을 고려해서dp를 갱신해주면 돼요.
[2], [3] 각 파이프의 종류에 따라서
dp를 갱신해줘요- 일단
가로파이프는 이전 파이프가가로,대각선인 경우만 설치할 수 있다고 했죠?- 이를 고려해서
dp값을 갱신해줍시다! - 지금은 현재 칸에 가로 파이프의 끝이 올거니까, [왼쪽 칸의
가로파이프 끝 개수]와 [왼쪽 칸의대각선파이프 끝 개수]를 더하면, [현재가로파이프의 끝 개수]가 되겠죠? (근데 실제로는 다0(아래 그림에서 노란색 칸dp)이여서 갱신한 값도 그대로0이네요~~)
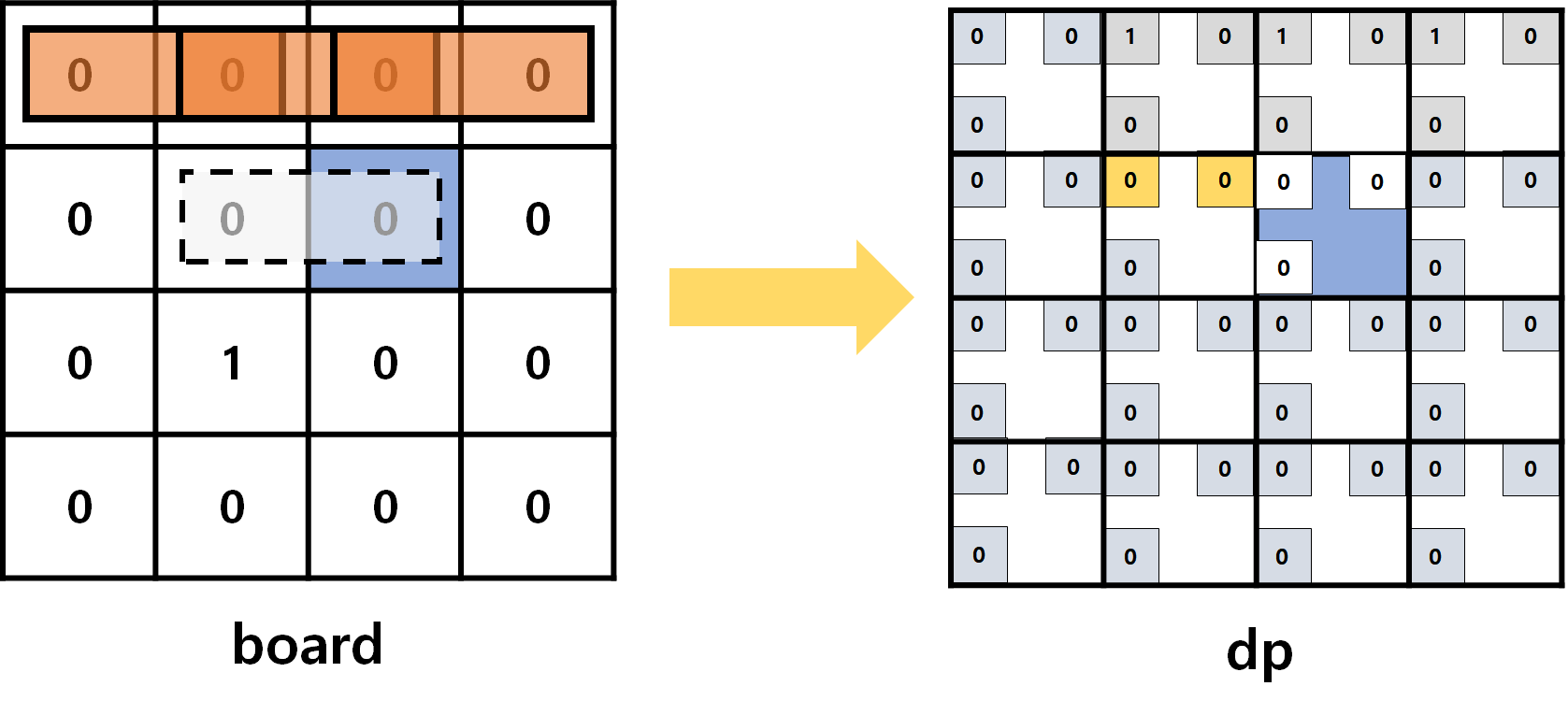
- 이를 고려해서
- 마찬가지로
세로파이프는,현재 칸의 세로 파이프의 끝 개수 = 위쪽 칸의 세로 파이프 끝 개수 + 위쪽 칸의 대각선 파이프 끝 개수가 될 것이고...
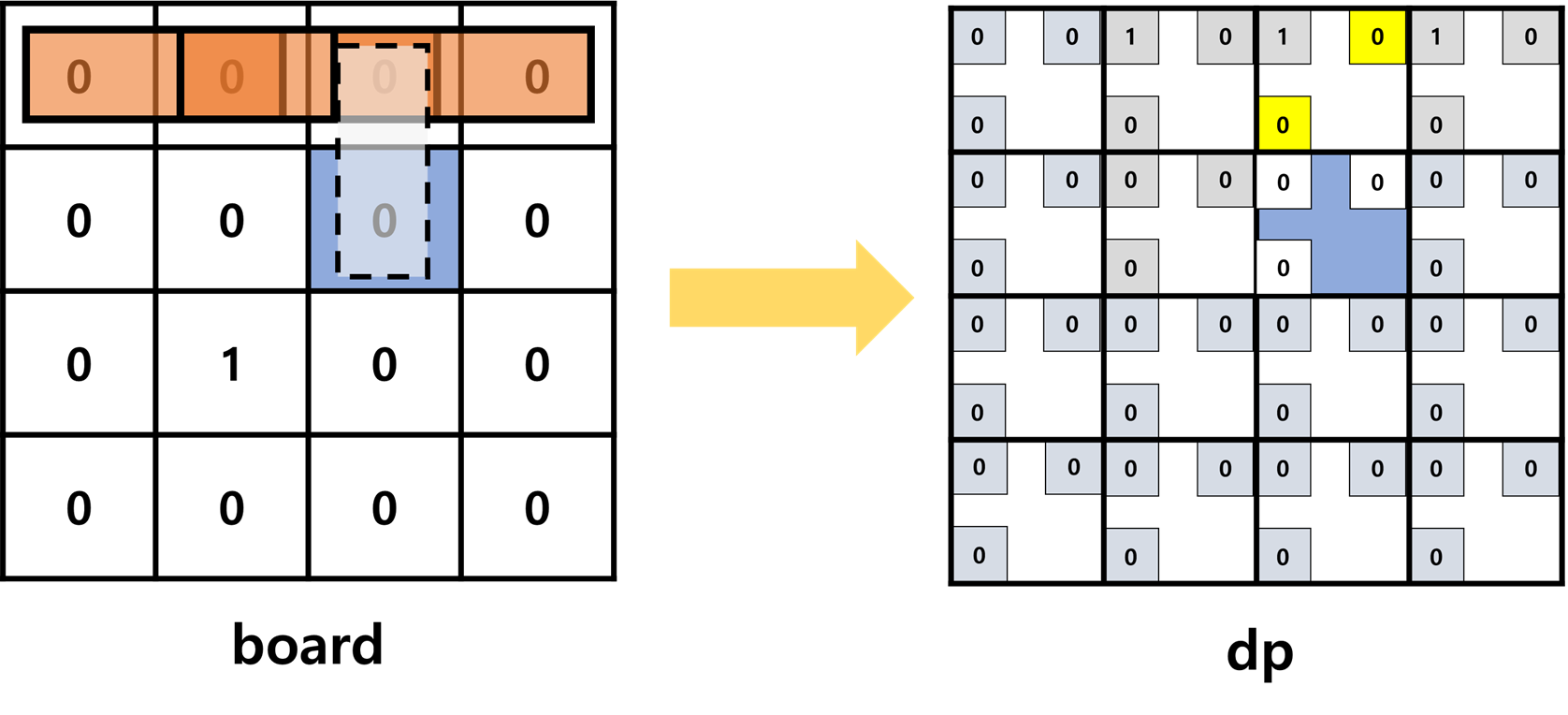
대각선파이프를 놓는 경우에 대해서는현재 칸의 대각선 파이프의 끝 개수 = (왼쪽 위 대각선)칸의 가로 파이프 끝 개수 + (왼쪽 위 대각선)칸의 세로 파이프 끝 개수 + (왼쪽 위 대각선)칸의 대각선 파이프 끝 개수)
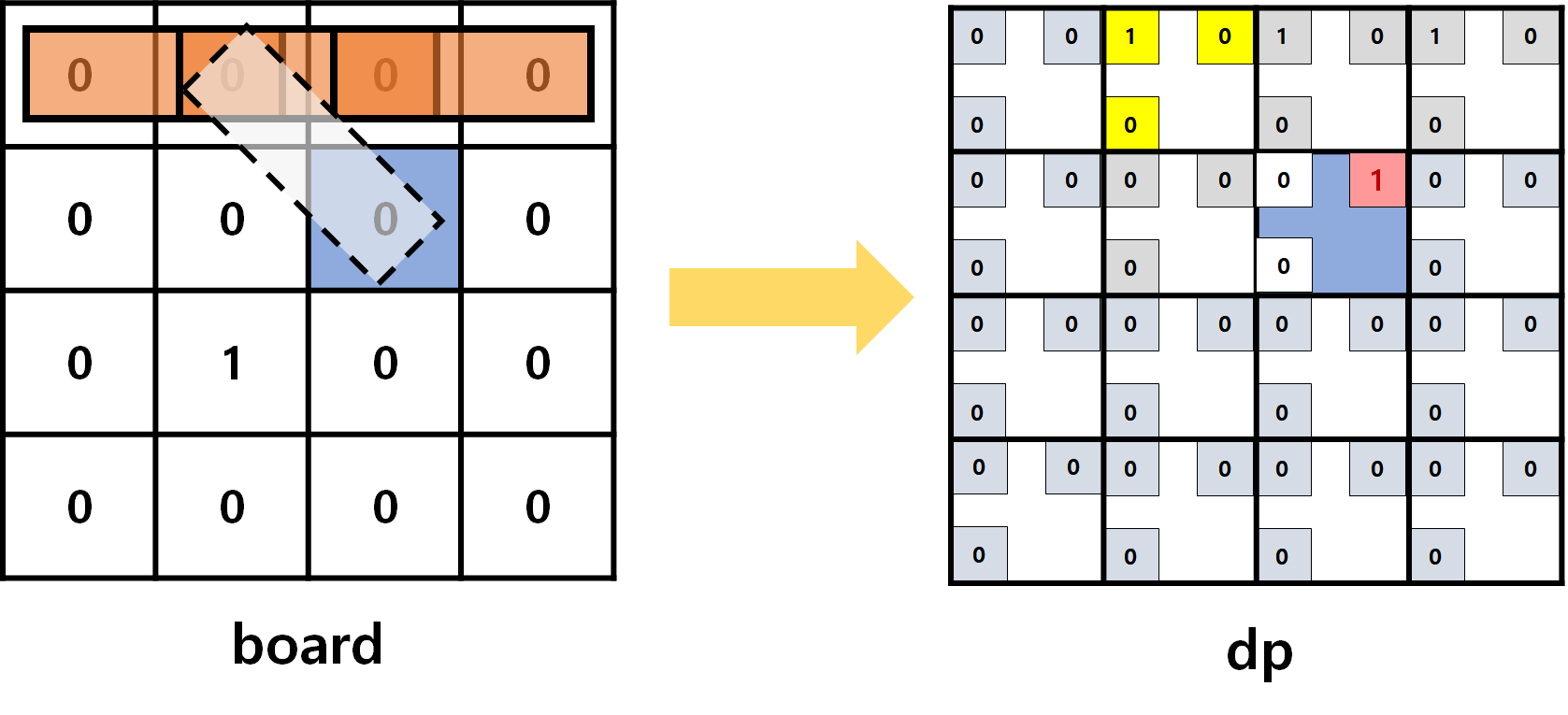
- 드디어 1이 갱신됐네요!
- 현재 우리가 검사하려고 하는 칸을 파란색으로 칠해봤어요.
-
이런 방법으로 계속해서
dp를 메모이제이션 방법으로 채워가시면 됩니다! -
코드는 아래와 같아요. 코드를 이해할때 주의할 점은
dp는가로,세로,대각선칸을 구현하기 위해 3차원 배열을 사용했어요. 설명은 아래에 써놨어요!dp[0][row][col]=가로파이프에 대한dpdp[1][row][col]=대각선파이프에 대한dpdp[2][row][col]=세로파이프에 대한dp
👏🏻 Code
# 0 → ─, 1 → /, 2 → |
def solution():
# 1행 미리 처리하기 → (3) 과정
dp[0][0][1] = 1
for i in range(2, N):
if board[0][i] == 0:
dp[0][0][i] = dp[0][0][i - 1]
# 왜 1행과 1열을 제외하는지는 (3), (4) 과정에서 봤었죠?
for r in range(1, N):
for c in range(1, N):
# (5) 과정
# 대각선 파이프를 추가하는 과정
if board[r][c] == 0 and board[r][c - 1] == 0 and board[r - 1][c] == 0:
dp[1][r][c] = dp[0][r - 1][c - 1] + dp[1][r - 1][c - 1] + dp[2][r - 1][c - 1]
# 가로, 세로 파이프를 추가하는 과정
if board[r][c] == 0:
dp[0][r][c] = dp[0][r][c - 1] + dp[1][r][c - 1]
dp[2][r][c] = dp[2][r - 1][c] + dp[1][r - 1][c]
# 최종 결과 출력
print(sum(dp[i][N - 1][N - 1] for i in range(3)))
N = int(input())
board = [list(map(int, input().split())) for _ in range(N)]
dp = [[[0 for _ in range(N)] for _ in range(N)] for _ in range(3)]
solution()

감사합니다ㅠㅠ 드디어 이해가 되네요