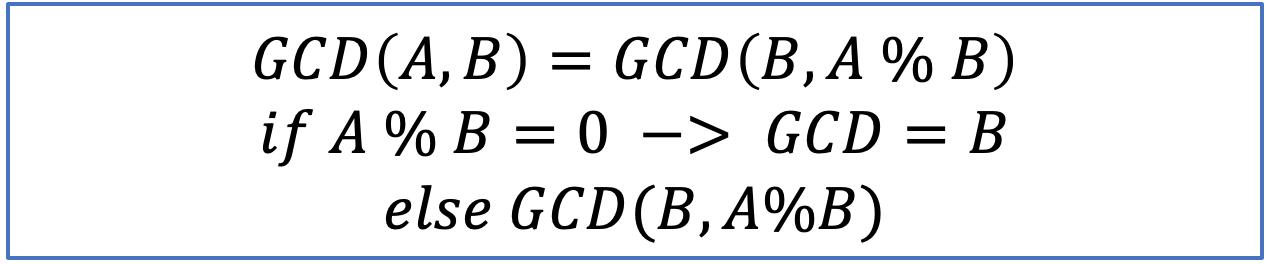📌 문제
📌 개념
- 최대 공약수와 최소 공배수 구하기
2개의 자연수를 받아 최대공약수를 받기 위해 2부터 두 자연수 중 작은 자연수까지 모두 나누어보면서 가장 큰 공약수를 구할 수 있다. 위와 같은 방법으로 문제를 풀면 시간복잡도는 O(N)이 된다.
- 유클리스 호제법
하지만 유클리드 호제법이란 알고리즘을 사용하면 시간복잡도를 O(logN)으로 줄일 수 있다.
유클리드 호제법이란?
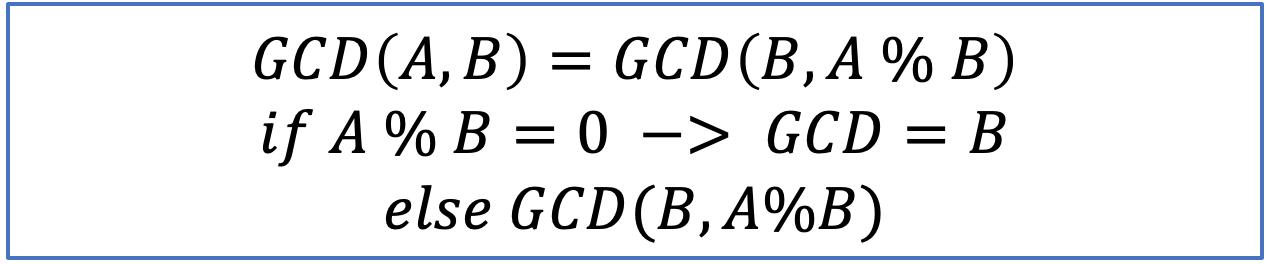
- 2개의 자연수의 최대공약수를 구하는 알고리즘이다.
- 2개의 자연수(또는 정식) a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다. 이 성질에 따라, b를 r로 나눈 나머지 r'를 구하고, 다시 r을 r'로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수이다. (출처: 유클리드 호제법)
📌 문제 해결
- 유클리드 호제법을 이용하여 최대공약수를 구한다.
- 입력한 2개의 숫자를 각각 a, b라고 하고, a와 b의 최대공약수를 GND라고 했을 때 최소공배수는 다음과 같이 구할 수 있다.
- GND×(a/GND)×(b/GND)=a×(b/GND)
Code
def GCD(n1, n2):
while n2 > 0:
temp = n2
n2 = n1 % n2
n1 = temp
return n1
n1, n2 = list(map(int, input().split()))
print(GCD(n1, n2))
print(int(n1 * n2 / GCD(n1, n2)))