다익스트라

개요

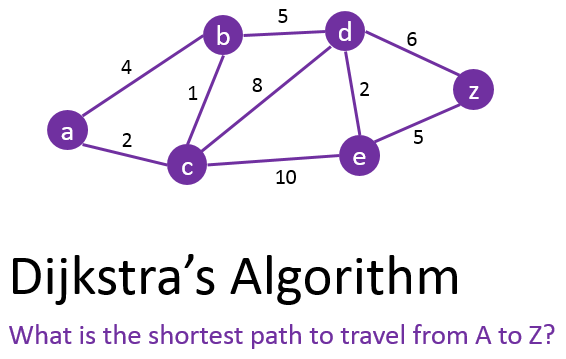
다익스트라 알고리즘은 가중치가 있는 그래프에서 한 시작 정점으로부터 다른 모든 정점까지의 최단 경로를 찾는 알고리즘이다. 특히, 간선의 가중치가 모두 양수일 때 유용하다.

다익스트라는 가중치가 서로 다른 그래프에서 주로 사용된다.

모든 간선의 가중치가 동일하다면 BFS
간선의 가중치가 0 또는 1일 때는 0-1 BFS
간선의 가중치가 음수라면 벨만 포드
모든 시작 정점에서 모든 다른 정점까지의 최단 경로를 구한다면 플로이드 와샬을 사용하는 것이 더 효율적이다.

다익스트라는 인접행렬이 아닌 가중치 인접행렬을 사용한다. 인접행렬은 간선이 없다면 값을 0으로 표시하지만 가중치 인접행렬에서는 간선이 없는 경우 INF 즉, 임의로 정한 매우 큰 값을 사용한다.

동작

1. 초기화

• 집합 S는 시작 정점 v로부터 최단 경로가 확정된 점들의 집합이다. 처음에는 v만 포함된다.

• distance 배열은 시작 정점 v로부터 다른 모든 정점까지 현재 알려진 최단 거리를 저장한다.

  • distance[v] = 0
  • distance[w] = weight[v][w] (정점 v to 정점 w 가중치)
  • 간선이 없다면 INF

2. 반복

• 집합 S에 포함되지 않는 정점들 중에서 distance값이 가장 작은 정점을 선택하여 S에 포함한다. 시작 정점으로부터 distance 값이 가장 작은 정점은 다른 정점을 경유하여 해당 정점을 방문하더라도 distance 값이 더 작을 수 없기 때문에 확정할 수 있다.

• 선택된 정점 u를 통해 다른 정점들의 distance값을 갱신한다.
  distance[w] = min(distance[w] , distance[u] + weight[u][w])
  이는 정점 u를 거쳐서 정점 w로 가는 경로가 기존의 distance[w]보다 짧으면 distance[w]를 갱신하는 과정이다.

3. 종료
   더이상 갱신할 수 있는 정점이 없거나, S에 모든 정점이 포함되면 종료한다.![]

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>

#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100
#define INF 1000000

typedef struct GraphType
{
	int N; // the number of node
	int weight[MAX_VERTICES][MAX_VERTICES];
};

int distance[MAX_VERTICES];
int found[MAX_VERTICES];

int choose(int distance[], int n, int found[])
{
	int min, minpos;
	min = INT_MAX;
	minpos = -1;
	for (int i = 0; i < n; i++)
	{
		if (distance[i] < min && !found[i])
		{
			min = distance[i];
			minpos = i;
		}
	}
	return minpos;
}

void print_status(GraphType* g)
{
	static int step = 1;
	printf("STEP %d: ", step++);
	printf("distance: ");
	for (int i = 0; i < g->N; i++)
	{
		if (distance[i] == INF)
			printf(" * ");
		else printf("%2d ", distance[i]);
	}
	printf("\n");
	printf(" found: ");
	for (int i = 0; i < g->N; i++)
		printf("%2d", found[i]);
	printf("\n\n");
}

void shortest_path(GraphType*g, int start)
{
	int u

	for (int i = 0; i < g->N; i++)
	{
		distance[i] = g->weight[start][i];
		found[i] = FALSE;
	}
	found[start] = TRUE;
	distance[start] = 0;

	for (int i = 0; i < g->N; i++)
	{
		print_status(g);
		u = choose(distance, g->N, found);
		found[u] = TRUE;
		for (int w = 0; w < g->N; w++)
		{
			if (!found[w])
				if (distance[u] + g->weight[u][w] < distance[w])
					distance[w] = distance[u] + g->weight[u][w];
		}
	}
}

백준 1753 최단경로
https://www.acmicpc.net/problem/1753

이 문제는 위의 방법처럼 배열을 이용해서 풀면 메모리 초과가 발생한다. MAX_VERTICES가 20,000이므로 weight 배열은 $20,000\times 20,000 \times 4byte$로 메모리 초과가 발생한다.

그러므로 우선 순위 큐를 이용해서 풀어야한다.