트리의 지름

알고리즘

1. 트리에서 임의의 정점 $r$ 를 선택한다.
2. 정점 $r$ 에서 가장 멀리 떨어진 정점 $x$ 를 선택한다.
3. 정점 $x$ 에서 가장 멀리 떨어진 정점 $y$ 를 선택한다.
4. $Dist(x,y)$ 는 트리의 지름이다.

증명

트리에서 정점 $u$ 와 $v$ 를 잇는 경로 $Dist(u,v)$ 를 실제 트리의 지름이라고 할 때,

1. $x$ 가 $u$ 또는 $v$ 인 경우

2. $y$ 가 $u$ 또는 $v$ 인 경우

3. $x$, $y$, $u$, $v$ 가 모두 서로 다른 경우

1번과 2번 케이스는 $x$ 또는 $y$ 가 $u$ 또는 $v$ 이므로 자연히 남은 한 점도 $u$ 또는 $v$ 이다.
$Dist(x,y) == Dist(u,v)$이다.

3번 케이스는 두가지 하위 케이스를 가진다.

3.1. $Dist(x,y)$ 와 $Dist(u,v)$ 경로가 한 점 이상 공유하는 경우

3.2. $Dist(x,y)$ 와 $Dist(u,v)$ 경로가 아무 점도 공유하지 않는 경우

3.1 케이스

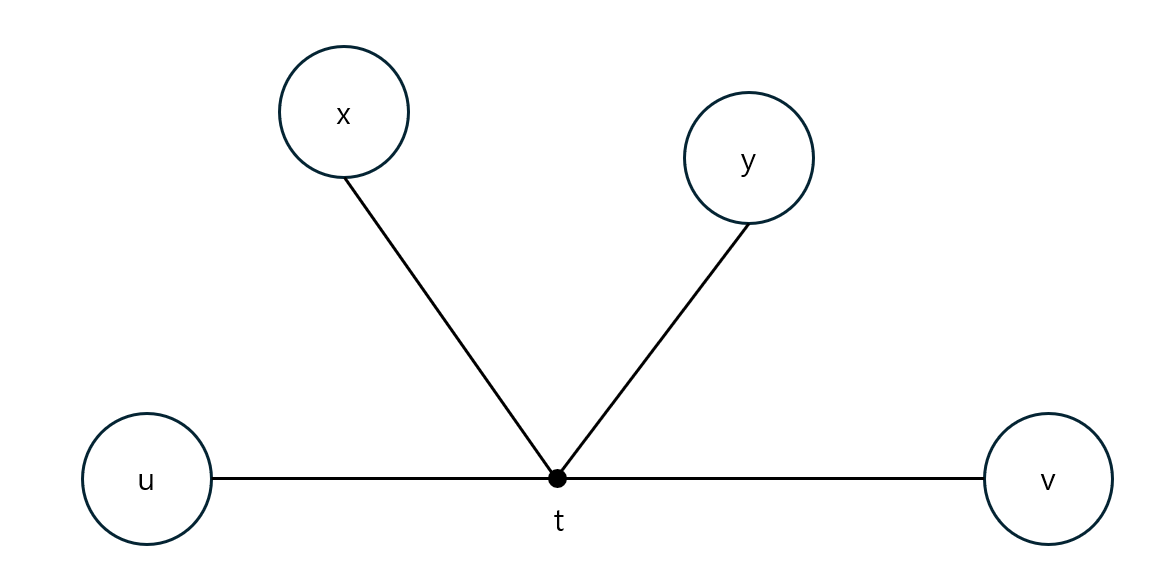
$Dist(x,y), Dist(u,v)$ 가 $t$ 라는 정점을 공유한다고 하자. 트리의 실제 지름이 $Dist(u,v)$ 인 상황에서 $Dist(u,v)$ 는 $t$ 라는 정점을 지나는 경로일 것이다.

즉, $t$ 정점에서 가장 멀리 떨어진 점이 $v$ 이다.
만약 $t$ 정점에서 가장 멀리 떨어진 정점이 $y$ 라면 트리의 실제 지름은 $Dist(u,y)$ 가 되므로 모순이 발생한다. 그러므로 $x$ 에서 가장 멀리 떨어진 정점인 $y$ 는 $t$ 를 기준으로 가장 멀리 떨어진 {$u$,$v$} 가 될 수 밖에 없다. 이에 따라 $x$ 도 정해진다.

3.2 케이스

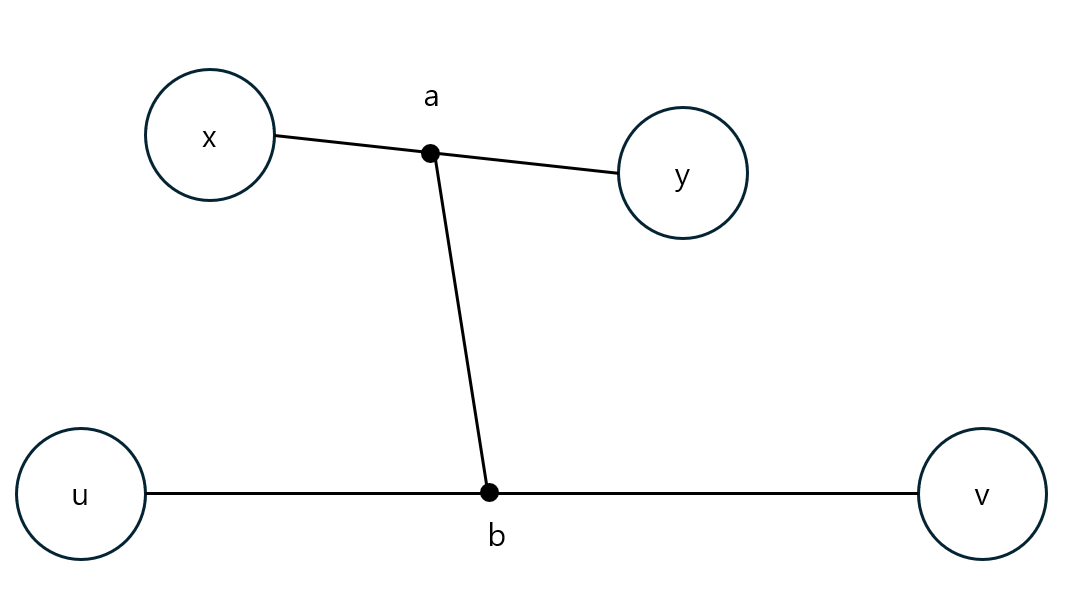
$Dist(x,y), Dist(u,v)$ 가 어떠한 점도 공유하지 않는 경우라도, 트리는 연결 그래프이므로 두 경로를 잇는 경로는 무조건 존재한다.

$x$ 에서 가장 멀리 떨어진 정점이 $y$ 이므로 $Dist(a,y) > Dist(a,b,v)$ 이다.
$u$ 에서 가장 멀리 떨어진 정점이 $v$ 이므로 $Dist(b,v) > Dist(b,a,y)$ 이다.

두 식을 엮으면,

$Dist(a,y) > Dist(a,b,v) > Dist(b,a,y)$
$Dist(a,y) > Dist(b,a,y)$ 는 모순이다. 즉, 3.2 케이스는 불가능하다.

위 케이스들을 통해서 임의의 정점 $x$ 를 잡고, 그로부터 가장 멀리 떨어진 정점 $y$ 를 선택하였을 때, $Dist(x,y)$ 는 결국 트리의 지름이 된다.

https://www.acmicpc.net/problem/1967