[백준 2118] 두 개의 탑

https://www.acmicpc.net/problem/2118

✍️ 첫번째 접근

예제 입력을 통해 문제를 해석하면 아래 그림을 만들 수 있다. 예시 하나를 든다면, 1번 지점부터 2번 지점까지 거리는 1이다.

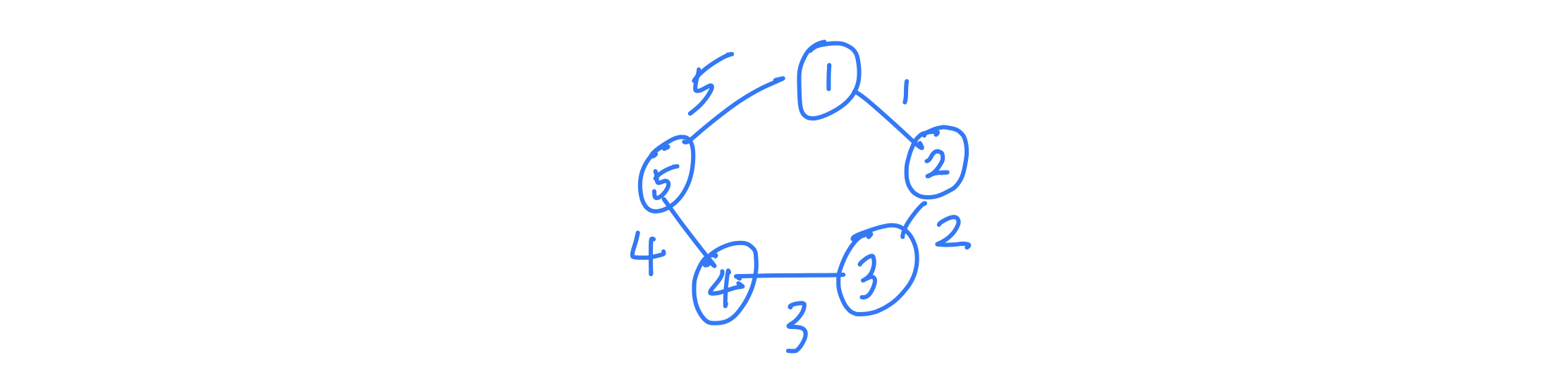
완전탐색으로 i지점부터 j지점까지 시계방향의 경로와 반시계반향의 경로를 구한 뒤, 그 둘 중에 최솟값을 answer에 넣는다. 모든 지점에 대하여 탐색을 끝냈으면 answer에 있는 값 중 최댓값을 출력하게끔 하였다. 논리에는 문제가 없다고 생각했지만 N이 최대 50000이므로 O(n^2)에다가 그 안에 합을 계산하기 위한 2개의 while문이 존재하므로 시간 초과가 발생하였다.

import Foundation

let n = Int(readLine()!)!
var arr: [Int] = []
for _ in 0..<n {
    let num = Int(readLine()!)!
    arr.append(num)
}
var answer: [Int] = []
for i in 0..<n {
    for j in i+1..<n {
        var forwardSum = arr[i]
        var backwardSum = 0
        var idx = i+1
        while idx < j {
            forwardSum += arr[idx]
            idx += 1
        }
        var cnt = n-j+i
        idx = i-1
        while cnt > 0 {
            if idx < 0 {
                idx = n-1
            }
            backwardSum += arr[idx]
            cnt -= 1
            idx -= 1
        }
        answer.append(min(forwardSum,backwardSum))
    }
}
print(answer.max()!)

✍️ 두번째 접근

먼저 i번째 지점을 1부터 N까지의 지점으로 정하지 않고 그 절반까지만 돌면 된다고 판단하였다. 그 이유는 시계방향의 경로와 반시계반향의 관계를 생각하면 된다.
또한, 경로를 매번 처음부터 구하는 경우를 누적합을 사용하여 구현하였다.
idx는 인덱스, arr은 입력으로 받은 값들을 저장한 배열, sum은 누적합을 저장한 배열이다.

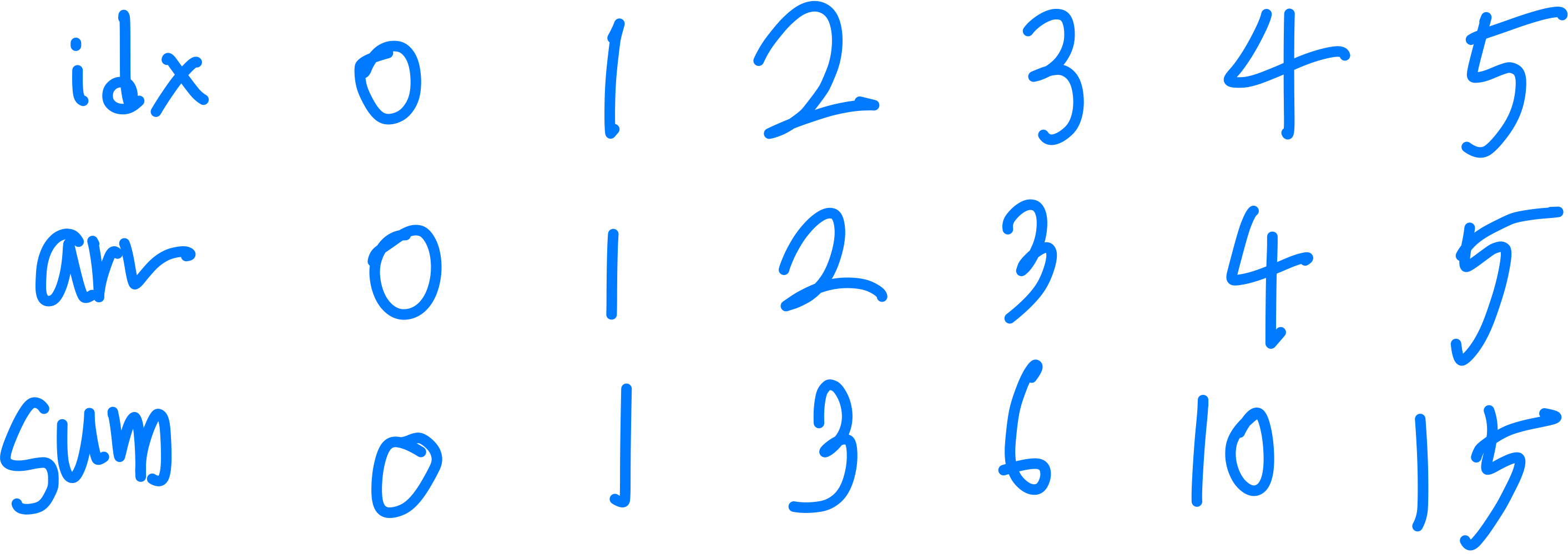
1번 지점부터 2번 지점까지의 경로를 생각해보자.
1번 지점부터 2번 지점까지 시계 방향의 경로는 (1번 지점부터 2번 지점까지의 누적합) - (1번 지점까지의 누적합)이다. 반시계 방향의 경로는 (1번 지점부터 5번 지점까지의 누적합) - (1번 지점부터 2번 지점까지의 누적합)이다.
즉, 시계 방향은 sum[1] - sum[0]이고 반시계 방향은 sum[5] - sum[1]이다.
이하 동문이다.

이해하기 더 쉽게 i번째 지점을 2로 해보자.
2번 지점부터 3번 지점까지의 경로를 생각해보자.
2번 지점부터 3번 지점까지 시계 방향의 경로는 (1번 지점부터 3번 지점까지의 누적합) - (2번 지점부터 1번 지점까지의 누적합)이다. 반시계 방향은 (1번 지점부터 5번 지점까지의 누적합) - (1번 지점부터 3번 지점까지의 누적합) + (1번 지점부터 2번 지점까지의 누적합)이다.
반시계 방향일 경우가 조금 까다로운데 수식 옆에 그림을 보면 그나마 이해하기 빠를 것이다.

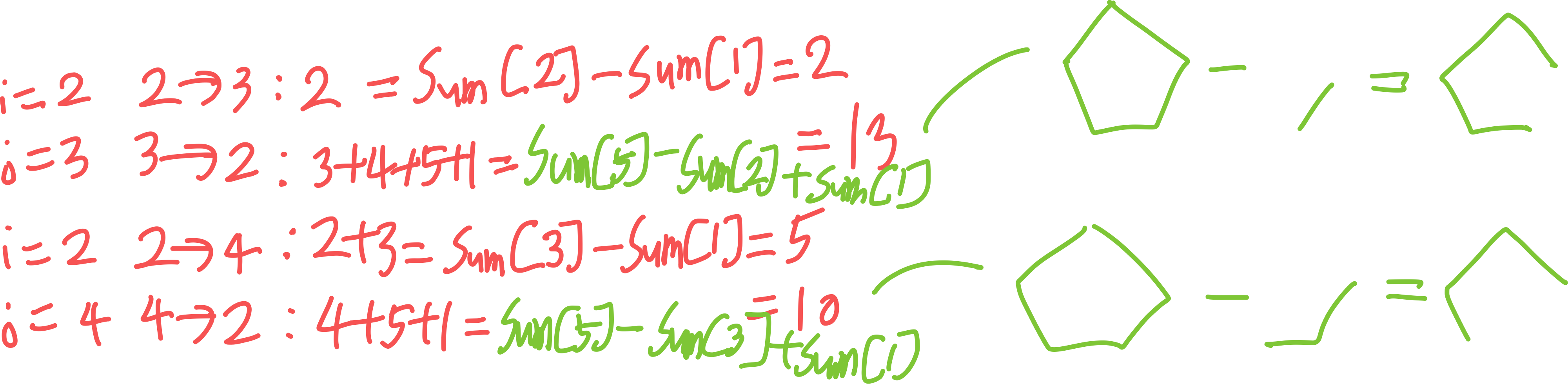
이렇게 하여 다음과 같은 일반항을 만들 수 있다.

시계 방향: sum[j-1]-sum[i-1]
반시계 방향: sum[n]-sum[j-1]+sum[i-1]

도출해낸 일반항으로 해결할 수 있었다. 얻은 점은, N의 범위를 보고 나서 시간 초과를 미리 예상해야한다는 것이고 같은 연산을 피하자는 것이다.

import Foundation

let n = Int(readLine()!)!
var arr: [Int] = Array(repeating: 0, count: n+1)
var sum: [Int] = Array(repeating: 0, count: n+1)
var answer = 0
for i in 1...n {
    arr[i] = Int(readLine()!)!
    sum[i] = sum[i-1]+arr[i]
}
for i in 1...n/2+1 {
    if i+1 > n {    // i+1이 n보다 크면 런타임 에러 발생하므로
        break
    }
    for j in i+1...n {
        answer = max(answer, min(sum[j-1]-sum[i-1],sum[n]-sum[j-1]+sum[i-1]))
    }
}
print(answer)