[CS] 자료구조

바인하·2022년 3월 27일

Tree

비선형 자료구조
계층적 관계 (Hierarchical Relationship) 를 표현하는 자료구조
트리를 구성하고 있는 요소들

Node : 트리를 구성하는 각각의 요소
Edge : 트리를 구성하는 노드들을 연결하는 선
Root Node : 트리 구조에서 최상위에 있는 노드
Terminal Node = Leaf Node = External Node (단말 노드) : 하위에 다른 노드가 연결되어 있지 않은 노드
Internal Node : 단말 노드를 제외한 모든 노드 (루트 노드 포함)

트리의 종류
1. Binary Tree
2. Full Binary Tree
3. Complete Binary Tree
4. BST (Binary Search Tree)

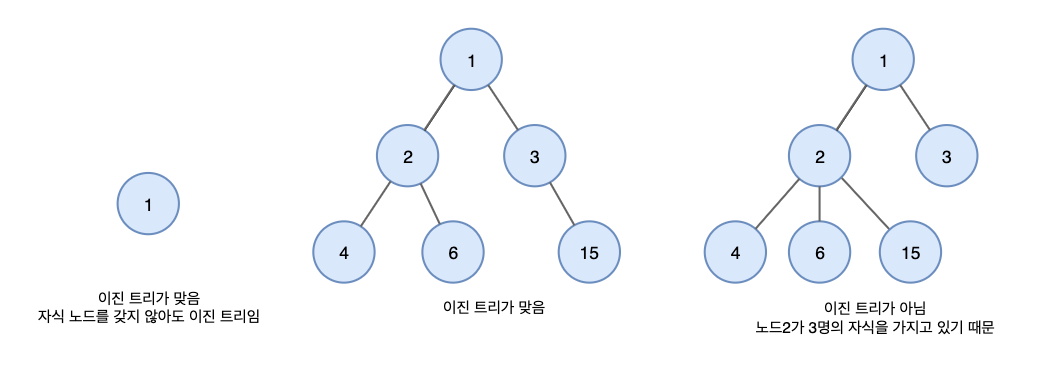
Binary Tree _ 이진트리

모든 노드들이 둘 이하의 자식을 가진 트리
루트 노드를 중심으로 2개의 서브트리 (큰 트리에 속하는 작은 트리) 로 나뉘어진다.
이 때, 나뉘어진 두 서브트리도 모두 이진 트리어야 한다.
공집합도 이진 트리로 포함된다.

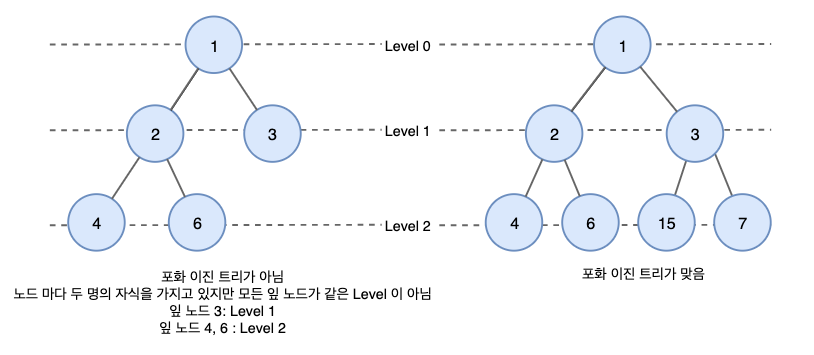
트리의 Level
0부터 시작하므로 루트 노드의 레벨은 0
트리의 최고 레벨은 해당 트리의 height (높이) 가 된다.

- Perfect Binary Tree (포화 이진 트리)
: 모든 레벨이 꽉 찬 이진 트리

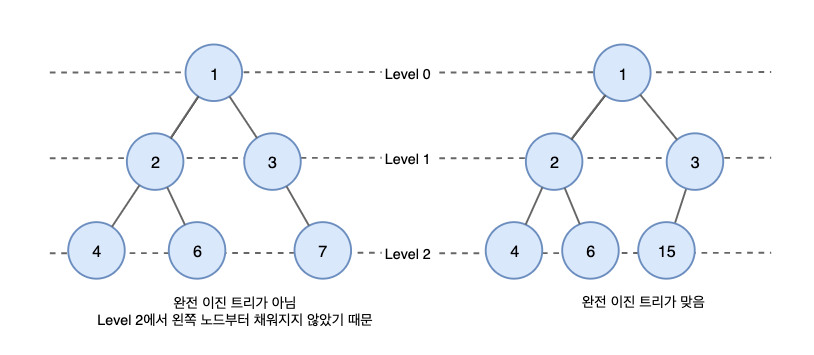
- Complete Binary Tree (완전 이진 트리)
: 위에서 아래로, 왼쪽에서 오른쪽으로 순서대로 채워진 이진 트리

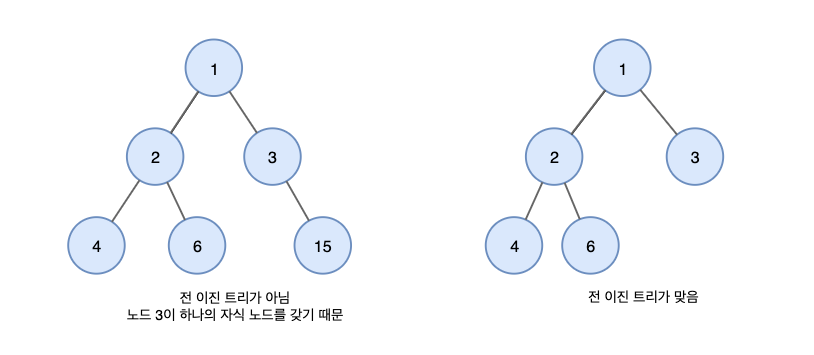
- Full Binary Tree (정 이진 트리)
: 모든 노드가 0개 or 2개의 자식 노드만을 갖는 이진 트리

BST (Binary Search Tree)

효율적인 탐색을 위해서는 '어떻게 찾을까' 를 고민하기보다 효율적인 탐색을 위한 '저장방법이 무엇일까' 를 고민해야 한다.

이진 탐색 트리에는 이진 트리의 일종이지만, BST에는 데이터를 저장하는 규칙이 있으며 이는 특정 데이터의 위치를 찾는데 사용할 수 있다.

규칙 1) BST의 노드에 저장된 키는 유일하다
규칙 2) 부모의 키 > 왼쪽 자식 노드의 키
규칙 3) 부모의 키 < 오른쪽 자식 노드의 키
규칙 4) 왼쪽, 오른쪽 서브 트리 == 이진탐색트리

이진 탐색은 원소가 정렬되어 있다는 조건 아래 정렬된 특징을 이용해 반 씩 쪼개가며 검색하므로, 검색 횟수가 획기적으로 낮아진다.
O(logN) 의 시간 복잡도를 갖는다.
저장 순서에 따라 한 쪽으로만 노드가 추가되면 Skewed Tree가 될 수 있어 이럴 경우 탐색의 Worst Case가 되어 O(n) 의 시간복잡도를 가진다.

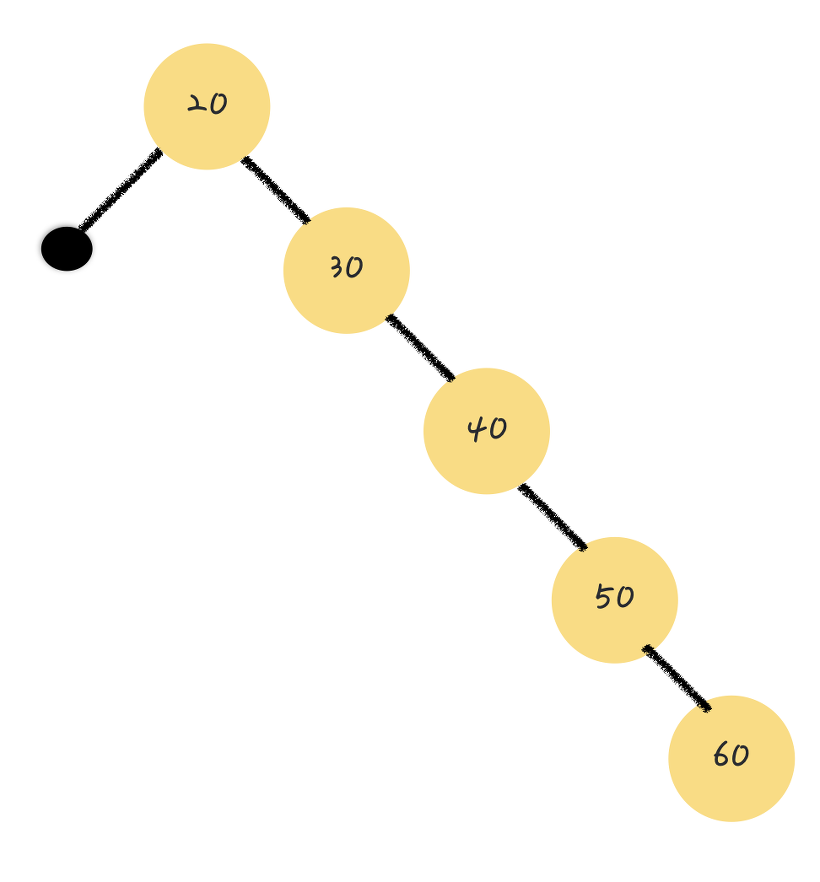
→ 이런 비효율적인 상황을 해결하기 위해 트리의 균형을 잡기 위한 재조정 Rebalancing 기법이 등장 ( 이를 구현한 트리가 Red-Black Tree )

이진탐색 트리의 목적 : 이진 탐색 + 연결리스트

이진 탐색 : 탐색 O(logN) / 삽입+삭제가 불가능
연결리스트 : 삽입, 삭제 O(1) / 탐색 O(N)
→ 두가지를 합하여 장점을 얻는 것이 이진 탐색 트리

효율적인 탐색 능력 + 자료의 삽입 삭제도 가능하게 만들자!

Binary Heap

트리 중에서도 배열에 기반한 Complete Binary Tree (완전 이진 트리)
배열에 트리 값을 넣어줄 때, 1번 index 부터 루트노드가 시작된다.
(노드의 고유번호 값과 배열의 index를 일치시켜 혼동을 줄이기 위함)

배열을 사용하여 효율적인 관리 가능!
= 즉, random access 가능

힙 : 최대힙 / 최소 힙
Max Heap : 각 노드의 값이 해당 children 의 값보다 크거나 같은 트리
- 루트 노드의 값이 가장 크기 때문에, 최댓값을 찾는데 소요되는 연산 O(1)
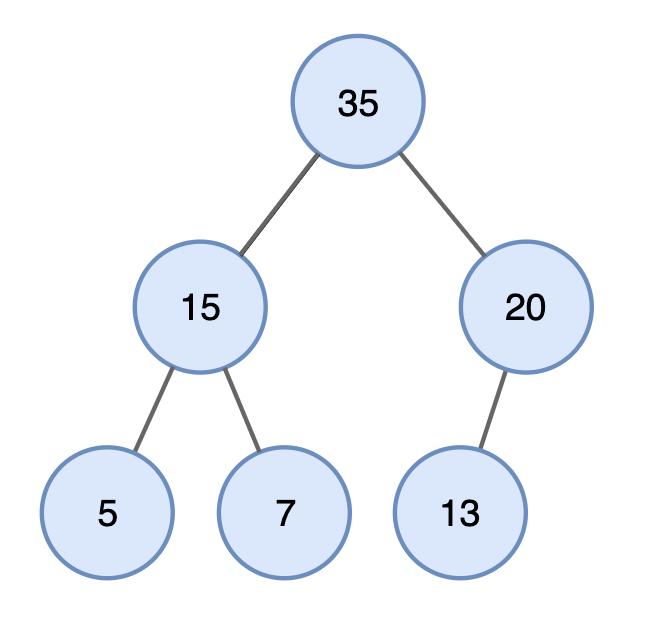
Min Heap : 각 노드의 값이 해당 children 의 값보다 작거나 같은 트리
- 루트 노드의 값이 가장 작기 때문에, 최솟값을 찾는데 소요되는 연산 O(1)
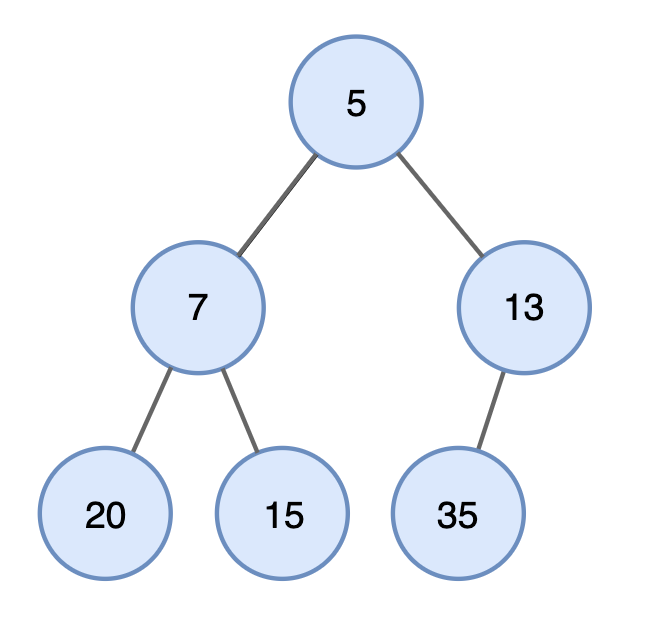
heap 의 구조를 유지하기 위해서는 제거된 루트 노드를 대체할 다른 노드가 필요
→ 맨 마지막 노드를 루트 노드로 대체시키고, heapify 과정을 거쳐 구조를 유지
결국 O(logN) 으로 최댓값, 최솟값에 접근할 수 있다.

Heapify 란? 이진트리에서 힙 속성을 유지하는 작업!

최대힙에서의 heapify 작업 순서

1. 요소 값과 자식 노드 값을 비교합니다.
2. 만약 자식 노드 값이 크다면 왼쪽 오른쪽 자식 중 가장 큰 값으로 교환합니다.
3. 힙 속성이 유지 될 때까지 1,2번 과정을 반복합니다.

Red Black Tree

https://zeddios.tistory.com/237

Binary Search Tree 를 기반으로 하는 트리 형식의 자료구조
탐색, 삽입, 삭제에 O(logN) 소요
동일한 노드의 개수일 때, depth를 최소화하여 시간 복잡도를 줄이는 것이 핵심!
Red Black Tree = Balanced Binary Search Tree
= Skewed tree 가 나오지 않도록 조건을 걸어두었음
= 균형이 잡혀있으므로, Skewed tree가 안나오므로 레드블랙트리의 높이는 logN 에 바운드 된다
= Search 연산은 O(logN)의 시간복잡도

1. 루트 노드: Black
2. External Node (Leaf Node) : Black
3. Internal : Red 노드의 자식은 Black (Red 연속해서 나올 수 없음)
4. 모든 리프노드에서 Black Depth 는 동일

최소 경로와 최대 경로 크기 비율 2 미만
ex) 최소 경로 - Black 노드만 있는 것
최대 경로 - B-R-B-R-B-R...

Hash Table

https://preamtree.tistory.com/20

Hash table : Key, Value를 갖는 자료구조
hash는 내부적으로 배열을 사용하여 데이터 저장하므로 빠른 검색 속도 가짐
특정한 값을 Search 하는데 데이터 고유의 인덱스로 접근하게 되므로 average case 에 대하여 Time Complexity 가 O(1)이 되는 것이다.(항상 O(1)이 아니고 average case 에 대해서 O(1)인 것은 collision 때문이다.)
인덱스로 저장되는 key 값이 불규칙하므로, 특별한 알고리즘을 이용하여 저장할 데이터와 연관된 고유한 숫자를 만들어 낸 뒤 이를 인덱스로 사용
- 특정 데이터가 저장되는 인덱스 = 그 데이터만의 고유한 위치
따라서, 삽입/삭제 시 추가적인 비용이 없음

특별한 알고리즘 이란? Hash Function

hashcode : hash method 또는 hash function 에 의해 반환된 데이터의 고유 숫자 값
저장되는 값들의 key 값을 hash function 을 통해 작은 범위 값으로 변경
Collision : 동일한 key 값에 복수 개의 데이터가 하나의 테이블에 존재할 수 있게 되는 것 / 서로 다른 2개의 키가 같은 인덱스로 hashing되면 같은 곳에 저장할 수 없게 됨

→ 그렇다면, 좋은 hash function 의 조건은?

일반적으로는, 키의 일부분이 아니라 키 전체를 참조하여 해쉬 값을 만들어내야 한다.
hash function을 무조건 1:1 로 만들기보다는 Collision을 최소화하는 방향으로 설계하고, Collision에 어떻게 대응할 것인가가 더 중요함

Resolve Conflict

1. Open Address 방식 (개방 주소법)
- 해시충돌 발생 시 (즉, 삽입하려는 해시버킷이 이미 사용중인 경우) 다른 해시 버킷에 해당 자료를 삽입

Collision 발생 시, 데이터 저장할 장소를 찾아 다님
- Linear Probing
- Quadratic Probing
- Double Hashing Probing

2. Separate Chaining 방식 (분리 연결법)

속도 : Open Addressing < Separate Chaining
해시충돌이 잘 발생하지 않도록 보조 해시 함수를 통해 조정할 수 있다면 Worst Case 로 가는 빈도 줄일 수 있음
2가지 구현 방식 존재

연결리스트 (Linked List)
- 각각의 버킷들을 연결리스트로 만들어 Collision 발생시 해당 버킷의 list에 추가하는 방식
- 삽입/삭제가 간단
Tree (Red-Black Tree)

연결리스트 / 트리 사용을 결정하는 기준 = 하나의 해시 버킷에 할당된 key-value 쌍의 개수

트리는 기본적인 메모리 사용량 많으므로, 데이터 개수가 적다면 Linked List 사용하자

→ 그렇다면, 데이터가 적다는 의미는 어느 정도를 의미하는가?

6개, 8개 기준으로 결정한다 → 변경하는데 소요되는 비용을 줄이기 위해서!
ex) 버킷에 6개의 key-value 쌍이 있었는데 하나가 추가된 순간 linked list -> tree / 하나가 삭제된 순간 tree -> linked list
- 이런식으로 각각의 자료구조로 넘어가는 기준이 1이면, Switching 비용이 너무 많이 필요

Open Addressing vs Separate Chaining

Open Addressing
- 연속된 공간에 데이터 저장하므로 Separate Chaining 보다 캐시 효율이 높다.
- 데이터 개수가 충분히 적으면, Open Address 가 더 성능이 좋음
Separate Chaining
- Open Address 처럼 버킷을 계속해서 사용하지는 않기 때문에 테이블의 확장을 보다 늦출 수 있다.
- 보조해시 함수로 Worst Case에 가까워지는 경우를 줄일 수 있다.

해시 버킷 동적 확장(Resize)
- 해시 버킷의 개수가 적으면 메모리는 아끼지만, 해시 충돌로 인한 성능 손실이 발생
- HashMap 은 key-value 데이터 개수가 일정 개수 이상이면 해시 버킷 개수를 2배로 늘림

→ 여기서 일정개수 이상이란?

데이터 개수가 해시버킷 개수의 75% 될 때
load factor: 0.75

Graph

정점과 간선의 집합
Directed Graph / Undirected Graph

Degree : 각 정점에 연결된 Edge의 개수
- Outdegree : 각 정점으로부터 나가는 간선의 개수
- Indegree : 들어오는 간선의 개수
그래프를 구현하는 2가지 방법

인접행렬: 정방행렬 사용

해당하는 위치의 value 값을 통해 vertex 간의 연결관계 O(1) 으로 파악
edge 개수와 무관하게 v^2 의 공간복잡도
dense graph 표현할 때 적절한 방법

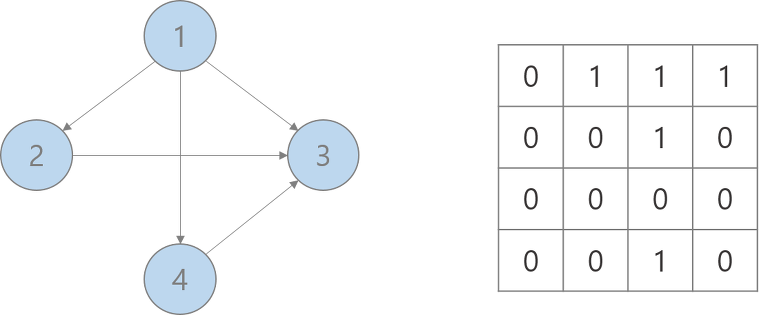
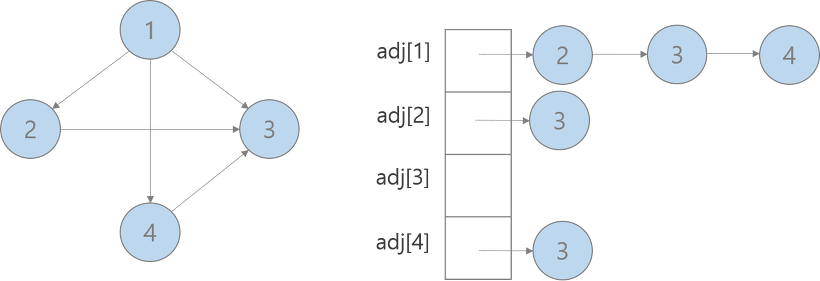
인접리스트: 연결리스트 사용

인접한 정점의 리스트를 확인해봐야 하므로 vertex 간 연결 여부 확인하는데 오래 걸림
공간 복잡도 O(E+V)
sparse graph 표현할 때 적절한 방법

그래프 탐색

1. 깊이 우선 탐색 (Depth First Search: DFS)

그래프 상에 존재하는 임의의 한 정점으로부터 연결되어 있는 한 정점으로만 나아간다
= 일단 연결된 정점으로 탐색하는 것
갔던 길을 되돌아오는 상황이 존재하는 미로찾기처럼 구성
Stack 사용
시간복잡도 : O(V+E)

2. 너비 우선 탐색 (Breadth First Search: BFS)

그래프 상에 존재하는 임의의 한 정점으로부터 연결되어 있는 모든 정점으로 나아간다.
Queue 사용 : 연락을 취할 정점의 순서를 기록하기 위한 것
- 탐색을 시작하는 정점을 Queue 에 넣는다.(enqueue)
- dequeue 를 하면서 dequeue 하는 정점과 간선으로 연결되어 있는 정점들을 enqueue 한다.

→ 즉, 정점들을 방문한 순서대로 queue에 저장하는 방법 사용

시간복잡도 : O(V+E)
BFS로 구한 경로는 최단 경로

Spaaning Tree 란? 
- 그래프 내의 모든 정점을 포함하는 트리
  = 그래프의 최소 연결 (간선의 수가 가장 적은) 부분 그래프
  = 그래프에서 일부 간선을 선택해서 만든 트리
- 모든 정점이 연결되어있어야 하며, 사이클을 포함해서는 안됨
- 그래프의 n개의 정점을 정확히 (n-1)개의 간선으로 연결

최소 신장 트리, MST (Minimum Spanning Tree)

Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리

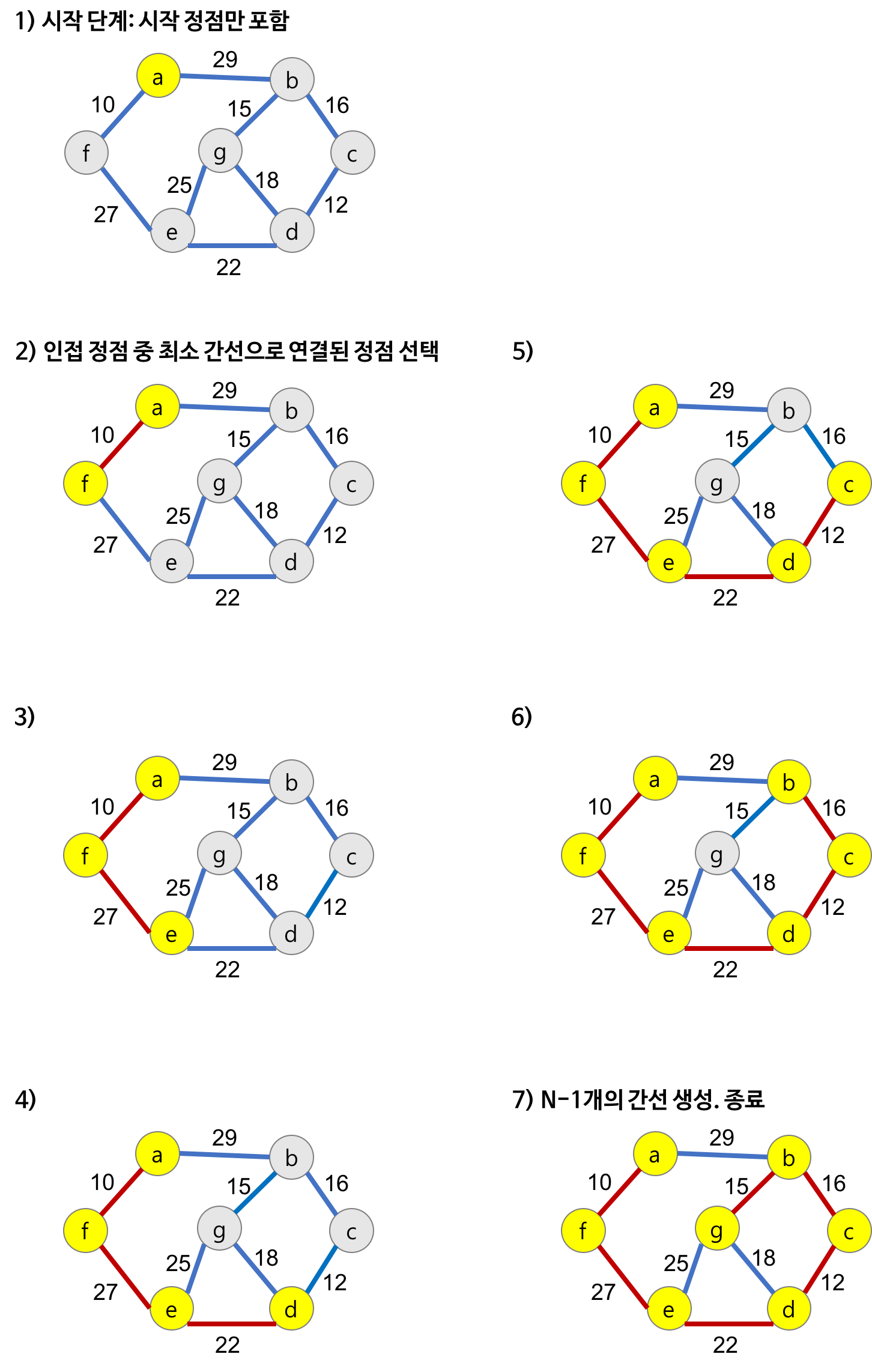
Kruskal Algorithm
https://gmlwjd9405.github.io/2018/08/29/algorithm-kruskal-mst.html

탐욕적 방법(greedy) 을 이용하여 가중치를 간선에 할당한 그래프의 모든 정점을 최소 비용으로 연결하는 최적 해답을 구하는 것

탐욕적 방법
- 그 순간에 가장 좋다고 생각되는 것을 선택함으로써 최종 해답에 도달하는 것
- 그 순간에는 최적이지만, 전체적으로 최적이라는 보장은 없음 _ 검증 과정 필요

간선 선택을 기반으로 하는 알고리즘
이전 단계에서 만들어진 신장트리와 관계없이 무조건 최소 간선만을 선택하는 방법
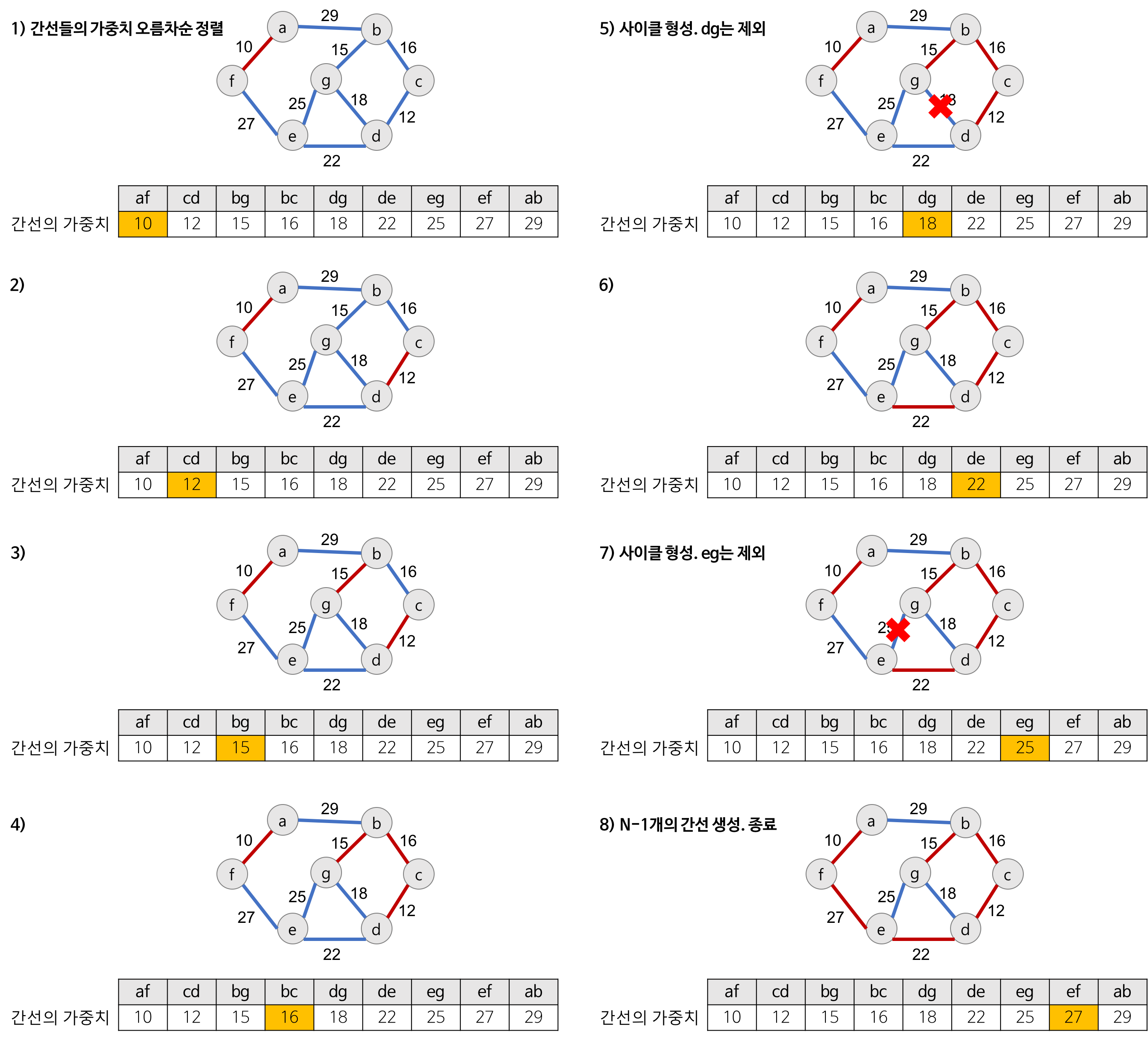
Kruskal 알고리즘의 동작

1. 그래프의 간선들을 가중치 오름차순으로 정렬
2. 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선 선택
3. 해당 간선을 MST 집합에 추가

→ Cycle 생성 여부를 판단하는 방법 : 추가하고자 하는 간선의 양 끝 정점이 같은 집합에 속해있는지 검사
- Graph 의 각 정점에 set-id라는 것을 추가적으로 부여
- 1~n 의 값으로 각각의 정점을 초기화
- 연결할 때마다 set-id를 하나로 통일시키는데, 값이 동일한 set-id 개수가 많은 set-id 값으로 통일