🧐 Path finding algorithms

1. Shortest Path

Shortest Path algorithm은 노드 사이의 최단 경로를 계산하는 것으로, 물리적 위치 사이의 경로를 찾거나 소셜 네트워크에서 사람들 사이의 상호 연결을 찾는 경우 등에 사용된다.

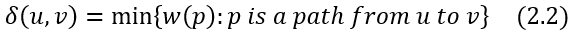
u에서 v까지의 최단 경로는 w(p)가 최소인 경로 p이다. 이때, u에서 v에 이르는 최단 경로의 Weight를 (2.2)와 같이 정의한다. 단, u에서 v에 이르는 경로가 없을 경우에는, δ(u, v) = ∞로 정의한다.

1-1. Single Source Shortest Path (SSSP)

임의의 한 노드 S에서 그래프의 다른 모든 노드까지의 최단 경로.
이 때, 간선의 가중치는 양수일 수도 있고, 음수일 수도 있다.

1-2. All Pairs Shortest Path (APSP)

그래프 내에서 모든 가능한 노드 쌍 사이의 최단 경로.

🙉 Practice in Neo4j!

1-1) 데이터 생성

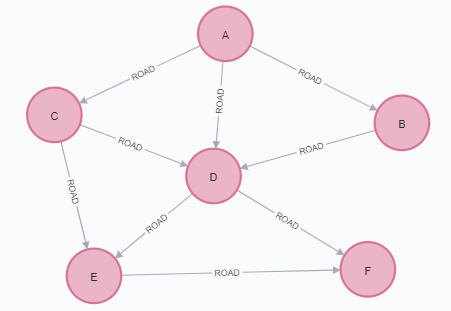
CREATE (a:Loc {name: 'A'}),
       (b:Loc {name: 'B'}),
       (c:Loc {name: 'C'}),
       (d:Loc {name: 'D'}),
       (e:Loc {name: 'E'}),
       (f:Loc {name: 'F'}),
       (a)-[:ROAD {cost: 50}]->(b),
       (a)-[:ROAD {cost: 50}]->(c),
       (a)-[:ROAD {cost: 100}]->(d),
       (b)-[:ROAD {cost: 40}]->(d),
       (c)-[:ROAD {cost: 40}]->(d),
       (c)-[:ROAD {cost: 80}]->(e),
       (d)-[:ROAD {cost: 30}]->(e),
       (d)-[:ROAD {cost: 80}]->(f),
       (e)-[:ROAD {cost: 40}]->(f);

1-2) A에서 F까지의 최단 경로 구하기

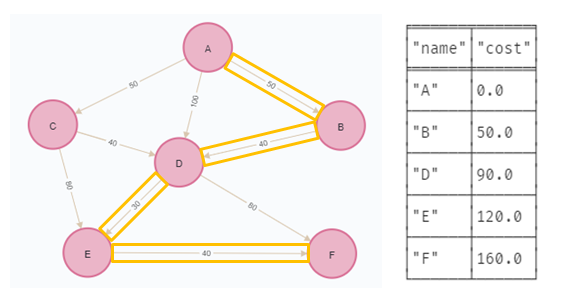
MATCH (start:Loc {name: 'A'}), (end:Loc {name: 'F'})
CALL gds.alpha.shortestPath.stream({
  nodeProjection: 'Loc',
  relationshipProjection: {
    ROAD: {
      type: 'ROAD',
      properties: 'cost',
      orientation: 'UNDIRECTED'
    }
  },
  startNode: start,
  endNode: end,
  relationshipWeightProperty: 'cost'
})
YIELD nodeId, cost
RETURN gds.util.asNode(nodeId).name AS name, cost

1-3) A의 SSSP

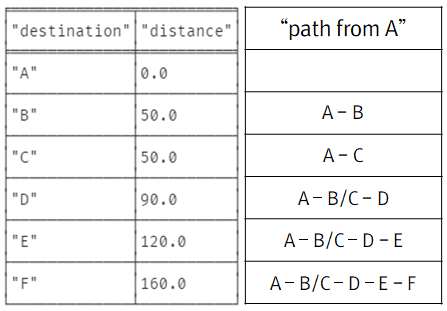
MATCH (n:Loc {name: 'A'})
CALL gds.alpha.shortestPath.deltaStepping.stream({
  nodeProjection: 'Loc',
  relationshipProjection: {
    ROAD: {
      type: 'ROAD',
      properties: 'cost'
    }
  },
  startNode: n,
  relationshipWeightProperty: 'cost',
  delta: 3.0
})
YIELD nodeId, distance
RETURN gds.util.asNode(nodeId).name AS destination, distance

1-4) APSP

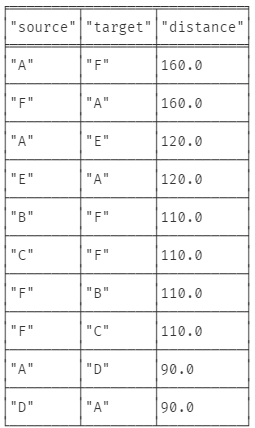
CALL gds.alpha.allShortestPaths.stream({
  nodeQuery: 'MATCH (n:Loc) RETURN id(n) AS id',
  relationshipQuery: 'MATCH (n:Loc)-[r:ROAD]-(p:Loc) RETURN id(n) AS source, id(p) AS target, r.cost AS cost',
  relationshipWeightProperty: 'cost'
})
YIELD sourceNodeId, targetNodeId, distance
WITH sourceNodeId, targetNodeId, distance
WHERE gds.util.isFinite(distance) = true

MATCH (source:Loc) WHERE id(source) = sourceNodeId
MATCH (target:Loc) WHERE id(target) = targetNodeId
WITH source, target, distance WHERE source <> target

RETURN source.name AS source, target.name AS target, distance
ORDER BY distance DESC, source ASC, target ASC
LIMIT 10

2. First Search

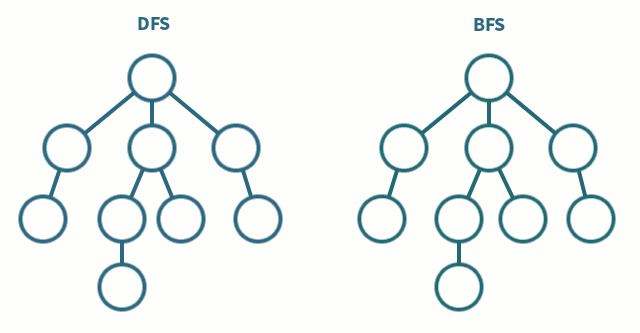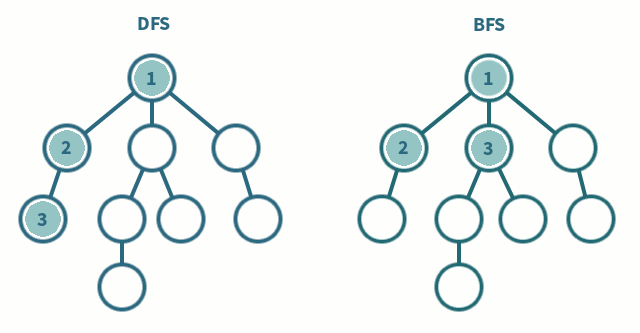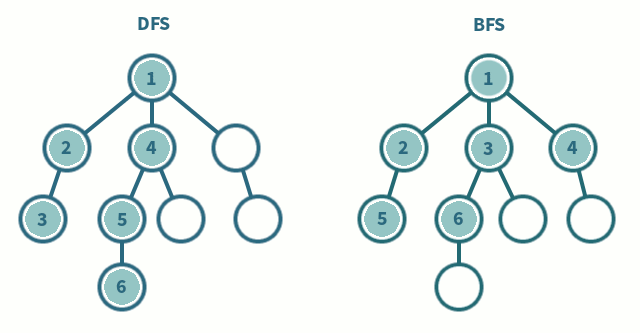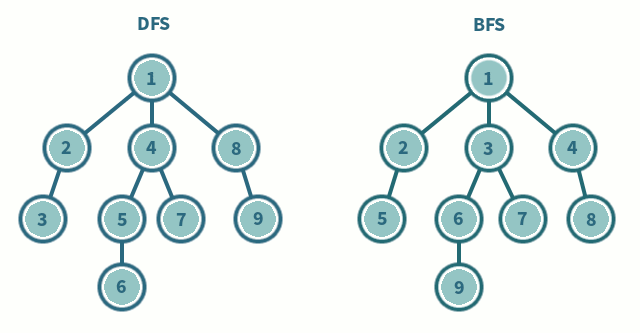
2-1. Breadth First Search (너비 우선 탐색, BFS)

루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하고, 멀리 떨어져 있는 정점을 나중에 방문하는 방법. 더 이상 방문하지 않은 정점이 없을 때까지 모든 정점들에 대해서 적용한다. 일반적으로 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 큐(Queue)를 사용한다.

2-2. Depth First Search (깊이 우선 탐색, DFS)

루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색한다. 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법이다. 일반적으로 스택(Stack)을 사용하여 구현하며, 너비 우선 탐색(BFS)보다 좀 더 간단하지만 단순 검색 속도 자체는 느리다.

🙉 Practice in Neo4j!

1) 데이터 생성

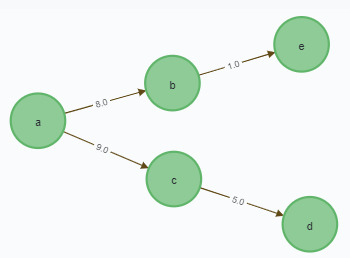
CREATE
       (nA:Node {tag: 'a'}),
       (nB:Node {tag: 'b'}),
       (nC:Node {tag: 'c'}),
       (nD:Node {tag: 'd'}),
       (nE:Node {tag: 'e'}),
       (nA)-[:REL {cost: 8.0}]->(nB),
       (nA)-[:REL {cost: 9.0}]->(nC),
       (nB)-[:REL {cost: 1.0}]->(nE),
       (nC)-[:REL {cost: 5.0}]->(nD)

2) A -> D : BFS

MATCH (a:Node{tag:'a'}), (d:Node{tag:'d'})
WITH id(a) AS startNode, [id(d)] AS targetNodes
CALL gds.alpha.bfs.stream({
	nodeProjection: 'Node',
    relationshipProjection: {
      REL: {
        type: 'REL',
        properties: 'cost'
      }
    },
	startNode: startNode,
    targetNodes: targetNodes,
    relationshipWeightProperty: 'cost'
})
YIELD path
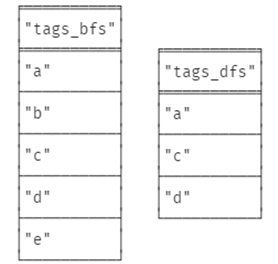
UNWIND [ n in nodes(path) | n.tag ] AS tags
RETURN tags
ORDER BY tags

3) A -> D : DFS

MATCH (a:Node{tag:'a'}), (d:Node{tag:'d'})
WITH id(a) AS startNode, [id(d)] AS targetNodes
CALL gds.alpha.dfs.stream({
	nodeProjection: 'Node',
    relationshipProjection: {
      REL: {
        type: 'REL',
        properties: 'cost'
      }
    },
	startNode: startNode,
    targetNodes: targetNodes,
    relationshipWeightProperty: 'cost'
})
YIELD path
UNWIND [ n in nodes(path) | n.tag ] AS tags
RETURN tags
ORDER BY tags

4) 결과