[묘공단] 코테 합격자되기 5주차

---

📌 9장 트리(자료구조)

📌💡 9-1. 트리 :

계층구조 ex) 파일 시스템이나 디렉터리 구조 등을 관리

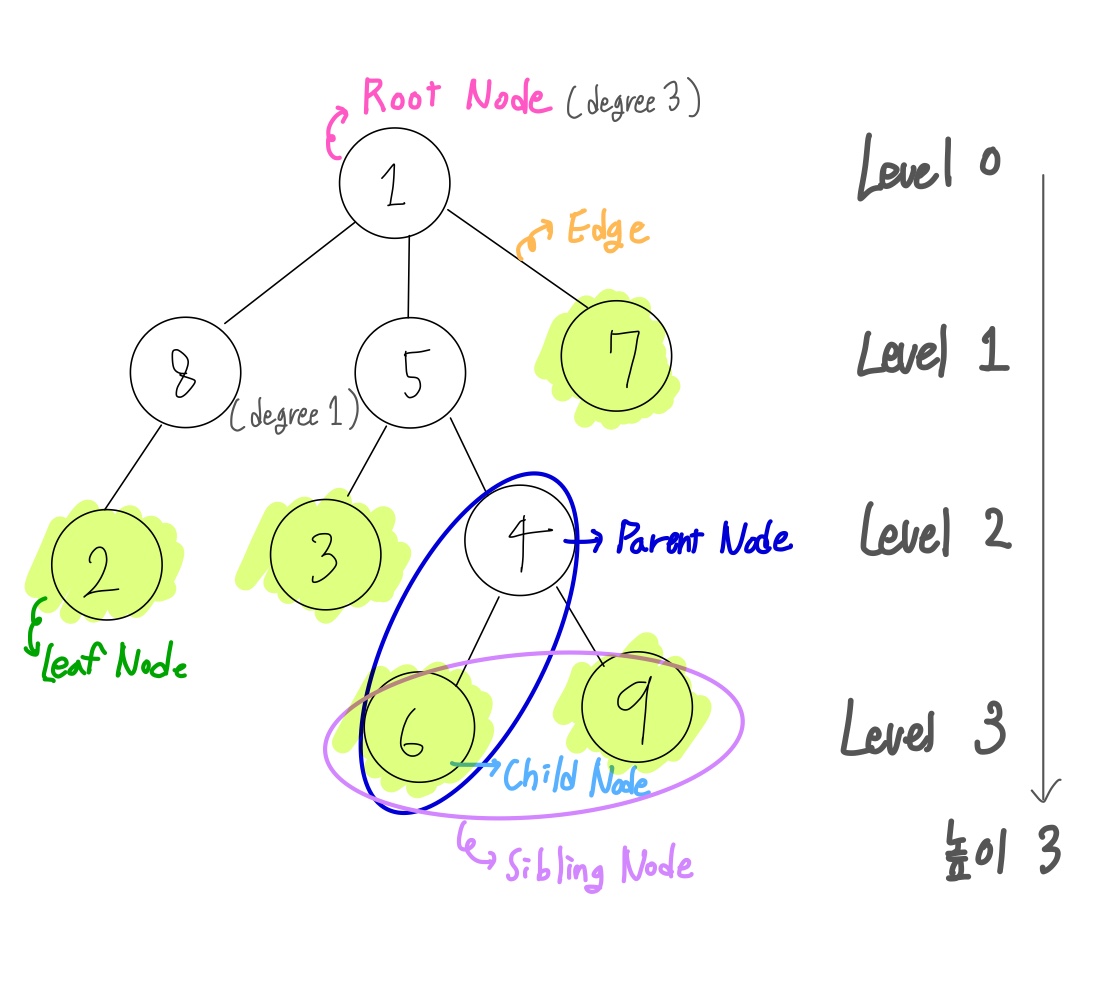
• 노드(Node) : 트리를 구성하는 요소
  * 루트 노드(Root node) : 노드 中 가장 위에 있는 노드
  • 부모 노드(Parent node) : 위에 있는 노드
  • 자식 노드(Child node) : 아래에 있는 노드
  • 형제 노드(Sibling node) : 같은 부모를 가지고 있는 노드
  • 리프 노드(Leaf node) : 자식이 없는 노드
• 엣지(Edge) : 노드와 노드를 이어주는 선
  * 트리 특징 :단방향 Edge, 루트 노드에서 각 노드로 가는 경로 유일
• 레벨(Level) : 루트 노드로 부터 특정 노드까지 거쳐가는 최소 간선 수
• 차수(Degree) : 특정 노드에 딸린 간선의 개수

📌💡9-2. 이진트리(binary tree) : 노드 한개 당 최대 2개의 자식노드

구현 방법 : 배열, 포인터

💡9-2-1. 이진트리(배열)

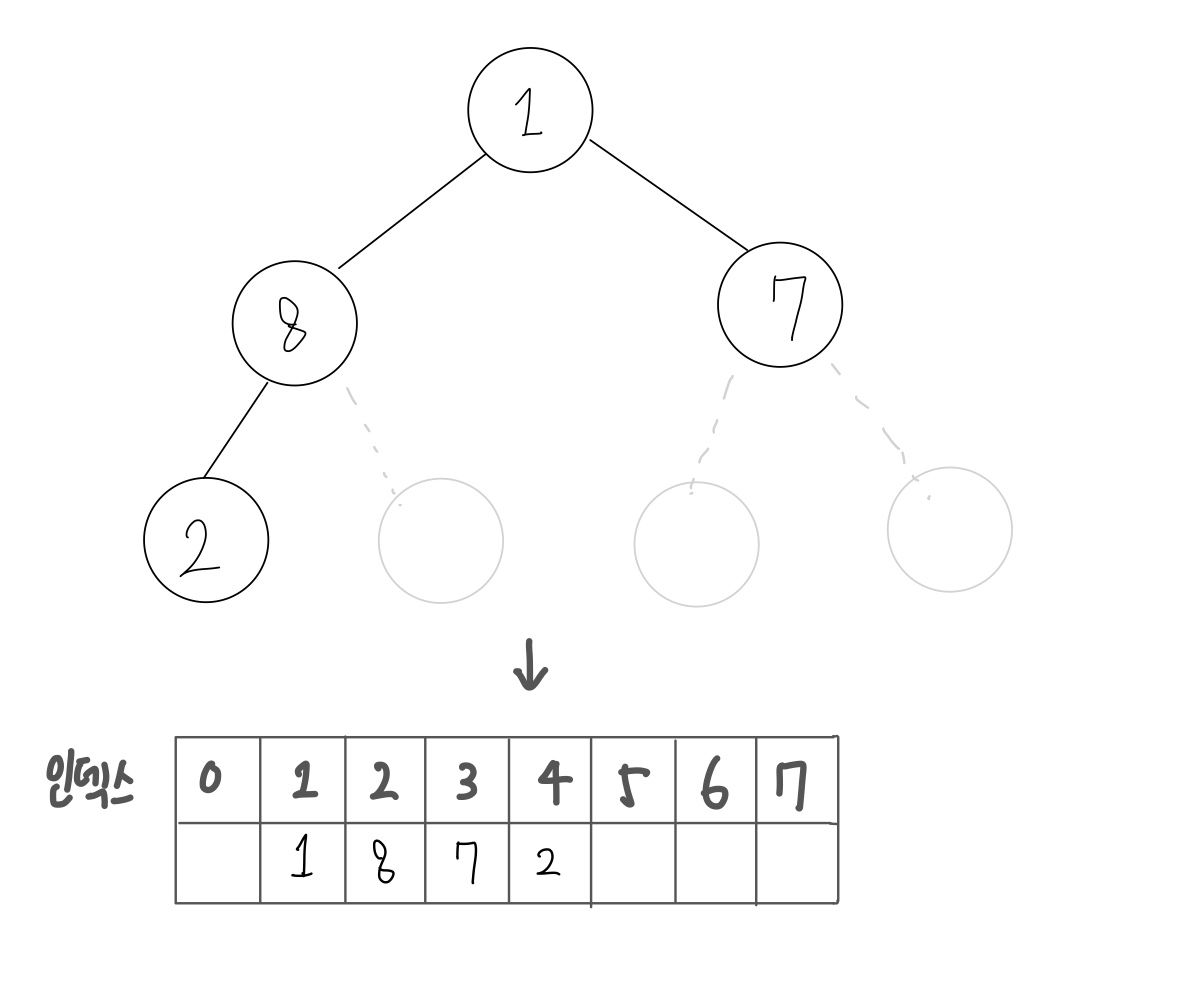
배열로 구현시

• 장점 : 구현 난이도 쉬움, 인덱스 존재하므로 메모리 넉넉시 추천
• 단점 : 배열로 표현 시 빈공간 多 (why? 노드의 부모-자식 관계를 곱셈 연산하여 인덱스 활용)
  -> 이진 트리 노드 N개일시, 시간복잡도 O(N) 발생
  

인덱스 1 설정시 > 추천 : 연산이 덜함

• 루트 노드 = 인덱스 1
• 왼쪽 자식 노드 = 부모 노드 인덱스 * 2
• 오른쪽 자식 노드 = 부모 노드 인덱스 * 2 + 1

인덱스 0 설정시

• 루트 노드 = 인덱스 1
• 왼쪽 자식 노드 = 부모 노드 인덱스 * 2 + 1
• 오른쪽 자식 노드 = 부모 노드 인덱스 * 2 + 2

💡 9-2-2. 이진트리(포인터)

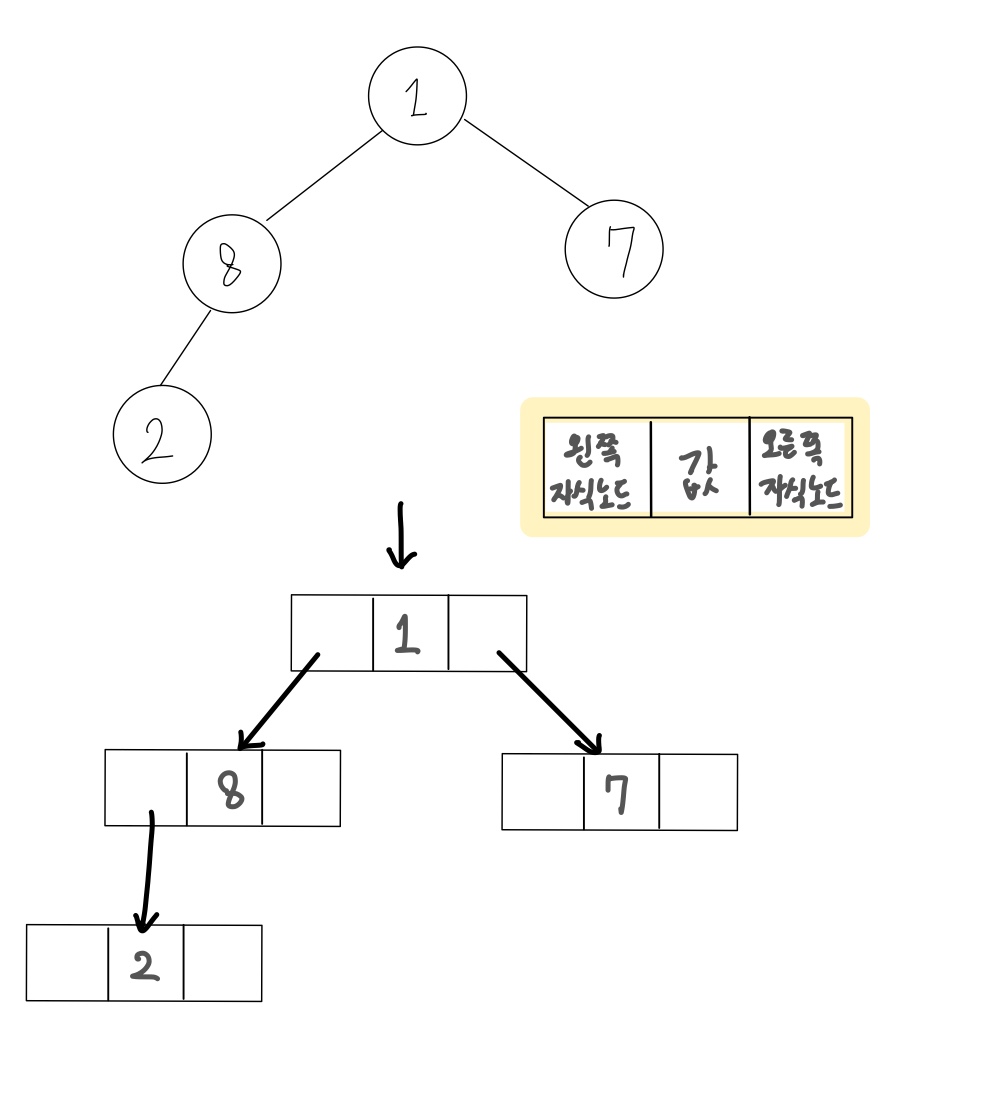
포인터로 구현시

• 장점 : 인덱스 존재 x -> 메모리 공간 낭비 없음
• 단점 : 노드를 따라가도록 구현, 구현난이도 上

순회 : 데이터를 빠짐 없이 방문 하는 것

• 방문 : 탐색을 마친 상태 <-> 이동 : 방문x, 지나가기만 함

💡 이진트리 순회 방법 3가지

순회시 방문 우선 순위 : 레벨이 높은 순 > 순회방법에 따라 다른 우선순위

• Preorder(전위 순회) - 트리 복사할 때 많이 사용
  현재노드 부모 노드일시,
  우선순위 : 부모 노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드
• inorder(중위 순회)
  현재노드 부모 노드일시,
  우선순위 : 왼쪽 자식 노드 -> 부모 노드 -> 오른쪽 자식 노드
• postorder(후위 순회)
  현재노드 부모 노드일시,
  우선순위 : 왼쪽 자식 노드 -> 오른쪽 자식 노드 -> 부모 노드

  이진 트리 구현시 가장 중요한 점

  원하는 노드 탐색을 효율적으로 할 수 있도록 트리 구현

📌💡 9-3. 이진탐색 트리 (binary search tree) : 노드 한개 당 최대 2개의 자식노드

구현 방법 : 배열, 포인터

이진 트리 구축시

• 데이터 크기를 따짐, 삽입과 동시에 정렬 진행

1. 데이터 크기 작을 때 : 왼쪽 자식 위치
2. 데이터 크기 같거나 끌때 : 오른쪽 자식 위치

이진 트리 탐색시

데이터 구축시 정렬했으므로,
각 노드의 차수와 노드 수가 비슷하면 : O(nlogN) 으로 판단 가능 == balanced binarary search tree (AVL 트리,레드 -블랙 트리존재)
비슷하지 않을 시 : 배열과 동일한 O(N)

1. 찾으려는 값이 현재 노드의 값과 같으면 탐색 종료, 크면 오른쪽 노드 탐색
2. 찾으려는 값이 현재 노드의 값보다 작으면 왼쪽 노드 탐색
3. 값을 찾으면 종료, 순회 완료시 값 없으면 현재 트리에 값 존재x로 판단

📌 9-3. 몸풀기 문제

🩶 문제 26. 트리 순회

주어진 데이터 : 배열
권장 시간 복잡도 : O(N)

제약조건 :

• 입력 노드값의 개수는 1개 이상, 1000개 이하이다.
• 노드값은 정수형이며, 중복되지 않는다.
• 전위, 중위, 후위 순위 반환하기

def preorder(nodes, idx):
  
  if idx < len(nodes):
    #전위 순회 : 부모 -> 왼쪽 -> 오른쪽
    ret = str(nodes[idx]) + " "#부모 노드(1부터 들어옴)
    ret += preorder(nodes, idx * 2)#왼쪽 자식 노드
    ret += preorder(nodes, idx * 2 + 1)# 오른쪽 자식 노드
    return ret
  # 재귀 종료
  else:
    return ""

def inorder(nodes, idx):
  if idx < len(nodes):
    #중위 순회 : 왼쪽 -> 부모 -> 오른쪽
    ret = inorder(nodes, idx * 2 )# 왼쪽 자식 노드
    ret += str(nodes[idx]) + " " # 부모 노드(1부터 들어옴)
    ret += inorder(nodes, idx * 2 + 1)# 오른쪽 자식 노드
    return ret
  else:
    return ""

def postorder(nodes, idx):
  if idx < len(nodes):
    #중위 순회 : 왼쪽 -> 오른쪽 -> 부모 
    ret = postorder(nodes, idx * 2 ) # 왼쪽 자식 노드
    ret += postorder(nodes, idx * 2 + 1)# 오른쪽 자식 노드
    ret += str(nodes[idx]) + " " # 부모 노드(1부터 들어옴)
    return ret
  else:
    return ""

def solution(nodes):
  return [
    preorder(nodes,1)[:-1], 
    inorder(nodes,1)[:-1], 
    postorder(nodes,1)[:-1], 
  ]


# TEST 코드 입니다. 주석을 풀고 실행시켜보세요
print(solution([1, 2, 3, 4, 5, 6, 7])) # 반환값 : ["1 2 4 5 3 6 7", "4 2 5 1 6 3 7", "4 5 2 6 7 3 1"]

쉬는 날,, 차주 업로드 예정,,,