Eigen value, Eigen vector

형준·2021년 1월 18일

Linear Algebra

목록 보기

3/6

벡터와 행렬연산

행렬은 벡터를 변환시킨다.

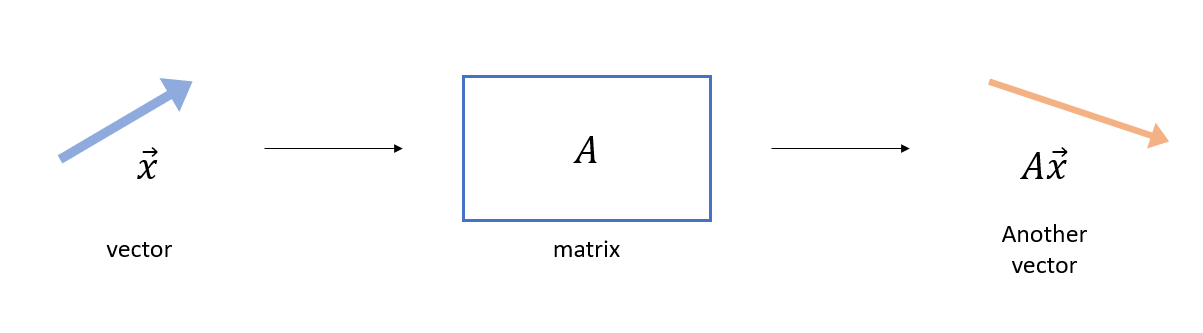
위의 그림처럼, 행렬을 이용해 벡터를 변환시켜주면 변환된 벡터 (A $\vec x$ )는 변환전과 비교했을때, 크기&방향이 모두 변할 수 있다.

Eigen Value, Eigen Vector

Tranformation은 matrix를 곱하는 것을 통해, 벡터(데이터)를 다른 위치로 옮긴다. 여기서 바뀌는 정도가 모두 다른데, 이러한 transformation에서 영향을 받지 않는 회전 축 (or 벡터) 를 고유벡터 (EigenVector)라고 한다.

고유벡터는 주어진 transformation에 대해서 크기만 변하고, 방향은 변하지 않는 벡터이다.
여기서 변화하는 크기는 결국 스칼라값인데, 이 특정 스칼라값을 고유값(Eigen value)라고 한다.

강의 내용

To start, consider some linear transformation in two dimensions, like the one shown in here
Eigen Vectors는 기저벡터에서부터 시작.

ex. $\hat{i} = \begin{bmatrix}3\\0\end{bmatrix} , \hat{j} = \begin{bmatrix}1\\2\end{bmatrix}$

so it's represented with a matrix, whose columns are (3,0) and (1,2)

이는 열이 (3,0),(1,2)인 행렬로 나타난다.

Think about the span of that vector, the line passing through its origin and its tip

벡터의 시점과 종점을 지나는 선인 span에 대해 생각해보자

대부분의 벡터는 변환의 과정에서 자신의 span을 벗어날것이다.

if the place where the vector landed also happens to be somewhere on that line.

But some special vectors do remain on their own span, meaning the effect that the matrix has on such a vectors is just to stretch it or squish it, like a scalar.

하지만 몇몇 특별한 벡터들은 고유한 스팬에 남아있다. 이것은 행렬은 이러한 벡터들이 마치 스칼라인것처럼 늘리고 줄이는 것 밖에 하지 않는다는 뜻이다

For this specific example, the basis vector i-hat is one such special vector.

이 특정한 예시에서는 기저벡터인 $\hat i$ 은 특별한 벡터이다.

The span of i-hat is the x-axis, and from the first column of the matrix

$\hat i$ 의 스팬은 x축이고, 행렬의 첫 열에서 나온것이다.

We can see that i-hat moves over to 3 times itself, still on that x axis.

3배 늘려도 x축위에있다.

What's more, because of the way linear transformations work, any other vector on the x-axis if also just stretched by a factor of 3.

또, 선형변환이 이뤄지는 방식때문에 x축 위의 다른 벡터도 3배로 늘어나고, 자신의 span에 남아있다.

비슷한 벡터로 [-1,1],이 있다. 이 벡터도 선형성으로 인하여 이 대각선 위에 있는 어떤 벡터도, 2배로 늘어나게될것을 알수있다. 변환 도중 다른 벡터들은 어떤식으로든 회전이 되어, 스팬하는 선 위를 벗어나게된다.