정렬 알고리즘

• 알고리즘 시간복잡도
  
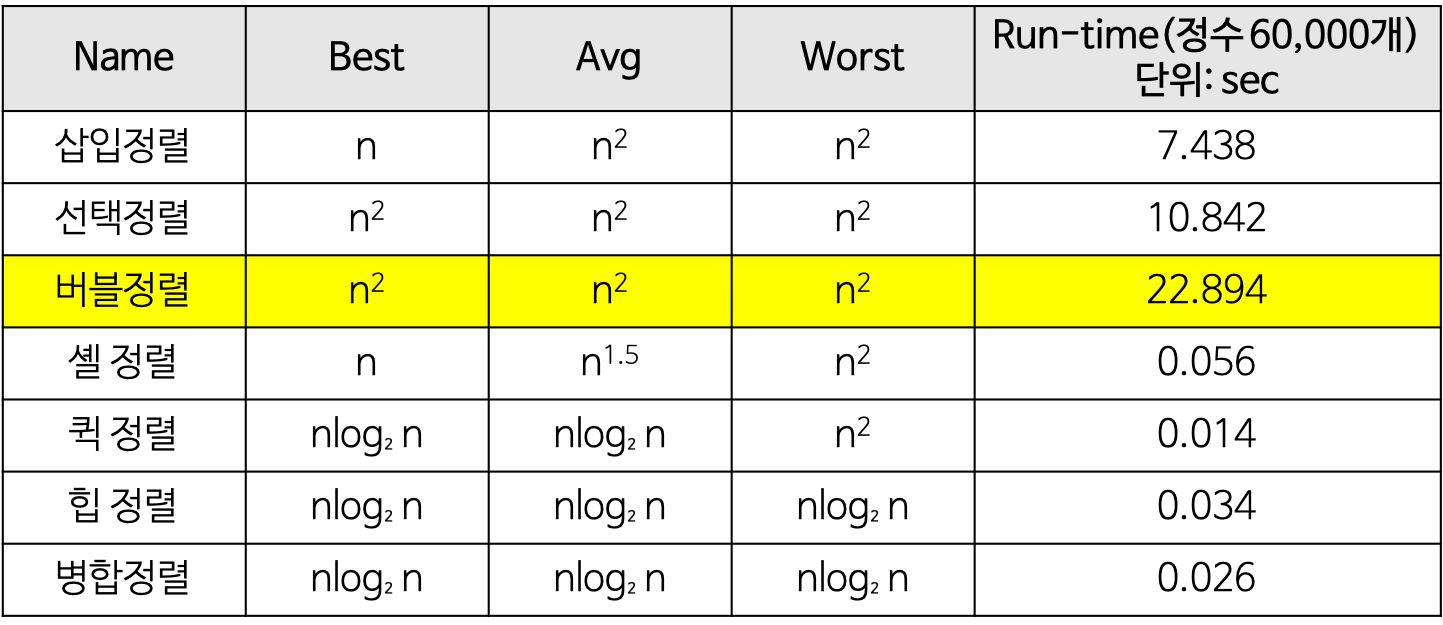
• 단순(구현 간단)하지만 비효율적인 방법 : 삽입 정렬, 선택 정렬, 버블 정렬
• 복잡하지만 효율적인 방법 :퀵 정렬, 힙 정렬, 합병 정렬, 기수 정렬

• 알고리즘 좋은 정리 사이트

1. zerocho 방송
2. 맛있는 프로그래머의 일상
3. 알고리즘

---

선택 정렬(Selection Sort), 삽입 정렬 (Insetion Sort), 버블 정렬 (Bubble Sort),
퀵 정렬 (Quick Sort), 병합 정렬 (Merge Sort), 기수 정렬(Radix Sort),
힙 정렬 (Heap Sort), 계수 정렬 (Counting Sort)

01 정렬 알고리즘 - 선택 정렬(Selection Sort)

02 정렬 알고리즘 - 삽입 정렬 (Insetion Sort)

03 정렬 알고리즘 - 버블 정렬 (Bubble Sort)

04 정렬 알고리즘 - 퀵 정렬 (Quick Sort)

05 정렬 알고리즘 - 병합 정렬 (Merge Sort)

06 정렬 알고리즘 - 기수 정렬(Radix Sort)

• 기수정렬 (Radix Sort)
  : 기수정렬은 낮은 자리수부터 비교하여 정렬해 간다는 것을 기본 개념으로 하는 정렬 알고리즘.
  • 장점: 기수정렬은 비교 연산을 하지 않으며 정렬 속도가 빠르다.
  • 단점 : 데이터 전체 크기에 기수 테이블의 크기만한 메모리가 더 필요.
  • 특징:
    1. 시간 복잡도는 O(dn) : d는 가장 큰 데이터의 자리수(d번 반복)
    2. 비교정렬 아니다. 같은 숫자라도 정렬할 때 순서가 섞이지 않는 안정 정렬.
  • 정렬 방식 :
    1. 0~9 까지의 Bucket(Queue 자료구조의)을 준비한다.
    2. 모든 데이터에 대하여 가장 낮은 자리수에 해당하는 Bucket에 차례대로 데이터를 둔다.
    3. 0부터 차례대로 버킷에서 데이터를 다시 가져온다.
    4. 가장 높은 자리수를 기준으로 하여 자리수를 높여가며 2번 3번 과정을 반복한다.
       // 핵심 : queue, 가장 낮은 자리수 -> 높은 자리수

07 정렬 알고리즘 - 힙 정렬 (Heap Sort)

08 정렬 알고리즘 - 계수 정렬 (Counting Sort)

• 계수 정렬(counting sort)
  : 모든 숫자의 개수를 센 후, 누적 합을 구하고, 다시 숫자를 넣어준다.
  • 적은 개수의 숫자를 정렬할 때 사용.
  • 비교정렬 아니다. 같은 숫자라도 정렬할 때 순서가 섞이지 않는 안정 정렬.
  • 단점 : 정렬할 때 추가적인 메모리(숫자 개수를 저장할 공간, 결과를 저장할 공간)가 필요, 가장 큰 숫자에 영향을 받는다.
  • 정렬 방식 :
    // [3,4,0,1,2,4,2,4], [개수를 저장할 공간], [결과]
  1. 개수를 저장할 공간을 정렬할 제일 큰 수의 갯수만큼 0으로 만들어줍니다.
     // [3,4,0,1,2,4,2,4], [0,0,0,0,0], [결과]
  2. 처음부터 개수를 세어 저장
     // [3,4,0,1,2,4,2,4], [1,1,2,1,3], [결과]
  3. 개수를 저장한 것을 누적합으로 바꿔준다.
     // [3,4,0,1,2,4,2,4], [1,2,4,5,8], [결과]
  4. 누적합을 바탕으로 숫자를 결과에 넣어준다. 누적합이 바로 숫자들의 인덱스 역할.
     // [3,4,0,1,2,4,2,4], [1,2,4,5,8], [0,1,2,2,3,4,4,4]
  • 시간복잡도 : 복잡도가 O(n + k).
    • k가 정렬할 수들 중에 가장 큰 값을 의미. 만약 k가 n보다 작은 수이면 O(n)이 되지만, k가 n보다 매우 큰 수이면 O(무한)이 될 수도 있다.
• 참고 설명
• 계수정렬 애니메이션 예시