[자료구조/알고리즘] Algorithm with Math

LEE JI YOUNG·2021년 12월 15일

자료구조/알고리즘

목록 보기

6/9

Algorithm with Math

알고리즘 문제를 푸는 방법 : 문제를 이해하고 어떻게 풀 것인지 전략을 세워서 어떤 알고리즘 기법을 사용할지 판단하기.
특정 방법을 사용해서 풀어달라는 문제는 수학적 사고 능력(컴퓨팅 사고 능력)을 보는 것.
알고리즘 문제에 자주 등장하는 수학적 개념
- 순열/조합
- GCD/LCM(최대공약수, 최소공배수)
- 멱집합

순열 / 조합

: 팩토리얼 사용

순열, 중복순열, 조합 - 재귀표현

순열(Permutation)

: n 개 중에서 일부(r)만을 선택하여 순서를 지키며 나열하는 것.

nPr = n! / (n-r)! (0! = 1, 1! = 1)

조합(Combination)

: n 개 중에서 일부(r)만을 선택하여 순서없이 나열하는 것.

nCr = n! / (r!*(n-r)!)
순열로 구할 수 있는 경우를 찾고, 순열로 구할 수 있는 경우에서 중복된 경우의 수를 나눔.

GCD / LCM

최대 공약수(GCD.Greatest Common Divisor)

: 둘 이상의 공약수 중에서 최대인 수.

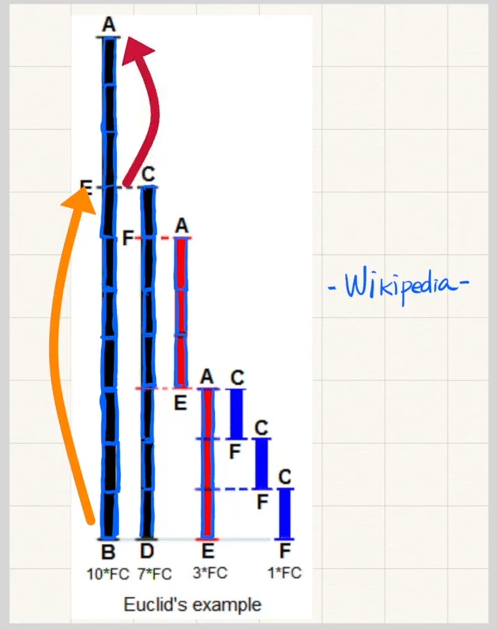
// 유클리드 호제법을 최대 공약수 구하기.
  function gcd(m, n) {
    if (m % n === 0) return n;
    return gcd(n, m % n);
  }

유클리드호제법의 원리

최소 공배수(LCM.Least Common Multiple)

: 둘 이상의 공배수 중에서 최소인 수.

멱집합

: 어떤 집합이 있을 때, 이 집합의 모든 부분집합을 멱집합이라 한다.

부분집합 갯수 : 2^n : 원소가 있는지, 없는지 2가지 경우를 고려하기 때문에 집합의 요소가 n 개일 때 모든 부분집합의 개수는 2^n개.
재귀사용 가능.

멱집합을 나열하는 방법.

: 집합 {1, 2, 3}
: 모든 부분집합 {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}

Step A: 1을 제외한 {2, 3}의 부분집합을 나열.
- Step B: 2를 제외한 {3}의 부분집합을 나열합.
  - Step C: 3을 제외한 {}의 부분집합을 나열. → {}
  - Step C: {}의 모든 부분집합에 {3}을 추가한 집합들을 나열. → {3}
- Step B: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열.
  - Step C: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열하려면, {}의 모든 부분집합에 {2}를 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {2, 3}을 추가한 집합들을 나열다. → {2}, {2, 3}
Step A: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열.
- Step B: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열하려면, {3}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {3}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열.
  - Step C: {3}의 모든 부분집합에 {1}을 추가한 집합을 나열하려면, {}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {1, 3}을 추가한 집합들을 나열. → {1}, {1, 3}
  - Step C: {3}의 모든 부분집합에 {1, 2}를 추가한 집합을 나열하려면, {}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {1, 2, 3}을 추가한 집합들을 나열. → {1, 2}, {1, 2, 3}
이 순서는, 트리구조와 비슷한 형태이다. 멱집합 문제는 트리 문제는 아닙니다. 그림은 이해를 돕기 위해 사용함.
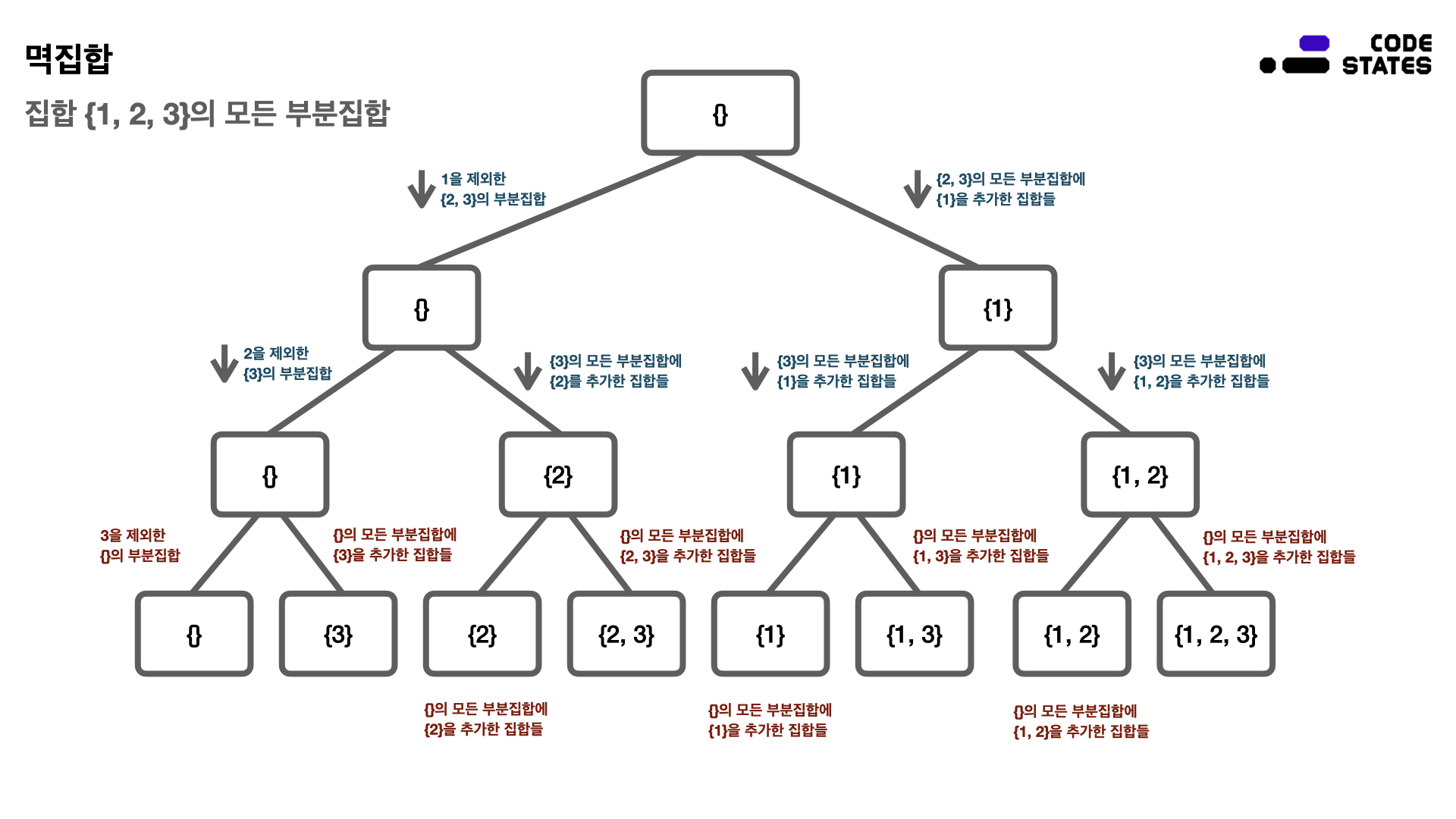
순환구조 : 멱집합을 구하는 방법에서 각 단계를 보면, 순환 구조를 띤다. 여기서 순환구조는 임의의 원소를 제외하면서 집합을 작은 단위로 줄여나가는 방법. 따라서, 문제를 작은 단위로 줄여나가는 재귀를 응용 가능. 문제가 가장 작은 단위로 줄어들고, 함수가 리턴될 때 카운트를 올리는 방식으로 멱집합의 개수를 구할 수 있다.