1. 오늘 일정

1) 강의 학습
2) 피어세션
3) 각 조별 피어세션 소개 시간

2. 학습 내용

AI 기초

7강: 통계학

모수란?

• 통계적 모델링은 적절한 가정 위에서 확률분포를 추정(inference)하는 것이 목표이다.
• 그러나 유한한 개수의 데이터만으로 모집단의 분포를 정확하게 알아내는 것은 불가능
  -> 근사적으로 확률분포를 추정

데이터가 틀정 확률분포를 따른다고 선험적으로 가정한 후 그 분포를 결정하는 모수(parameter)를 추정하는 방법을 모수적(parametric) 방법론이라 한다.

특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌면 비모수(nonparametric) 방법론이라 부른다.

• 기계적으로 확률분포를 가정해서는 안 되며, 데이터를 생성하는 원리를 먼저 고려하는 것이 원칙이다.

정규분포 모수 추정 해보기

• 정규분포의 모수는 평균 $\mu$와 분산 $\sigma^2$으로 이를 추정하는 통계량(statistic)은 다음과 같다.

표본평균 : $\overline{X} = \frac{1}{N}\sum\limits_{i=1}^{N}X_i$
표본분산 : $S^2 = \frac{1}{N-1} \sum\limits_{i=1}{N}(X_i-\overline{X})^2$

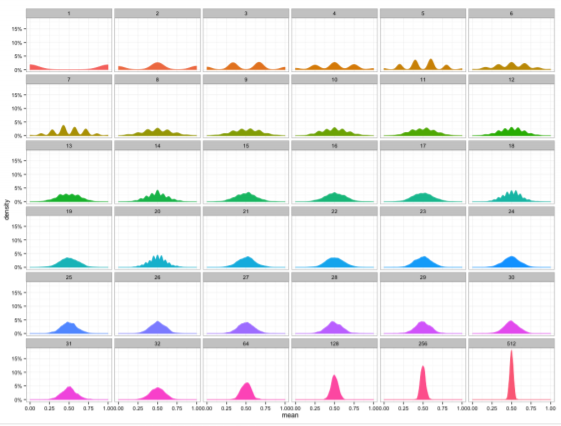
• 통계량의 확률분포를 표집분포(sampling distribution)라 부르며, 특히 표본평균의 표집분포는 $N$이 커질수록 정규분포 $N(\mu, \sigma^2/N)$를 따른다. 다음은 그에 대한 예시이다.

최대가능도 추정법

• 이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나는 최대가능도 추정법(maximum likelihood estimation, MLE)이다.

$\widehat{\theta}_{MLE} = \text{argmax} \, L(\theta;x) = \text{argmax} \, P(x|\theta)$

• 데이터 집합 $x$가 독립적으로 추출되었을 경우 로그가능도를 최적화한다.

왜 로그가능도를 사용하는가?

• 데이터의 숫자가 수억 단위가 된다면 컴퓨터의 정확도로 가능도 계산은 불가능하다.
• 따라서 데이터가 독립일 경우, 로그를 사용하면 가능도의 곱셈을 로그가능도의 덧셈으로 바꿀 수 있게 되므로 컴퓨터로 연산이 가능하다.
• 특히, 경사하강법으로 가능도를 최적화할 때 미분 연산을 사용하게 되는데, 로그가능도를 사용하면 연산량을 $O(n^2)$에서 $O(n)$으로 줄여준다.$

최대가능도 추정법 예제: 정규분포

$log L(\theta;x) = \sum \limits_{i=1}^{n}logP(x_i|\theta) = \sum \limits_{i=1}^{n}log\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{\left| x_i-\mu \right|^2}{2\sigma^2}} = -\frac{n}{2}log2\pi\sigma^2-\sum\limits_{i=1}^{n}\frac{\left| x_i-\mu \right|^2}{2\sigma^2}$

$0 = \frac{\partial logL}{\partial \mu} = - \sum \limits^{n}_{i=1} \frac{x_i-\mu}{\sigma^2}$
$0 = \frac{\partial logL}{\partial \sigma} = -\frac{n}{\sigma}+\frac{1}{\sigma^3}\sum \limits_{i=1}^{n} \left| x_i - \mu \right|^2$

• 두 미분이 모두 0이 되는 $\mu, \sigma$를 찾으면 가능도를 최대화하게 된다.

$0 = \frac{\partial logL}{\partial \mu} = - \sum \limits^{n}_{i=1} \frac{x_i-\mu}{\sigma^2}$ $\, \,\;$=> $\, \,\;$ $\widehat\mu_{MLE}= \frac{1}{n}\sum \limits_{i=1}^{n}x_i$
$0 = \frac{\partial logL}{\partial \sigma} = -\frac{n}{\sigma}+\frac{1}{\sigma^3}\sum \limits_{i=1}^{n} \left| x_i - \mu \right|^2$ $\, \,\;$=> $\, \,\;$ $\widehat\sigma^2_{MLE}= \frac{1}{n}\sum \limits_{i=1}^{n}(x_i-\mu)^2$

최대가능도 추정법 예제: 카테고리 분포

$\widehat\theta_{MLE} = \argmax\limits_{p_1 ,\cdots,p_d} \,logP(x_i|\theta) = \argmax\limits_{p_1 ,\cdots,p_d} \, log(\prod \limits_{i=1}^{n} \prod \limits_{k=1}^{d} p_k^{x_i,k})$

• 카테고리 분포의 모수는 다음 제약식을 만족해야 한다. (확률질량함수이기 때문에)

$\sum \limits_{k=1}^{d}p_k = 1$

$\widehat\theta_{MLE} = \argmax\limits_{p_1 ,\cdots,p_d} \,logP(x_i|\theta) = \argmax\limits_{p_1 ,\cdots,p_d} \, log(\prod \limits_{i=1}^{n} \prod \limits_{k=1}^{d} p_k^{x_i,k})$
$log(\prod \limits_{i=1}^{n} \prod \limits_{k=1}^{d} p_k^{x_i,k}) = \sum \limits_{k=1}^{d}(\sum \limits_{i=1}^{n}x_i,k)\, log p_k$
$n_k = \sum \limits_{i=1}^{n}x_i,k$

$log(\prod \limits_{i=1}^{n} \prod \limits_{k=1}^{d} p_k^{x_i,k}) = \sum \limits_{k=1}^{d}(n_k \, log \, p_k) \quad \text{with} \quad \sum \limits_{k=1}^{d}p_k = 1$

• 오른쪽 제약식을 만족하면서 왼쪽 목적식을 최대화하는 것이 우리가 구하는 MLE이다.

$log(\prod \limits_{i=1}^{n} \prod \limits_{k=1}^{d} p_k^{x_i,k}) = \sum \limits_{k=1}^{d}(n_k \, log \, p_k) \quad \text{with} \quad \sum \limits_{k=1}^{d}p_k = 1$
$\Rightarrow \, \, \, \mathcal{L}(p_1, \cdots,p_k, \lambda) = \sum \limits_{k=1}^{d} n_k \, log \, p_k +\lambda(1-\sum \limits_kp_k)$

• 라그랑주 승수법을 통해 최적화 문제를 풀 수 있다.

$\Rightarrow \, \, \, \mathcal{L}(p_1, \cdots,p_k, \lambda) = \sum \limits_{k=1}^{d} n_k \, log \, p_k +\lambda(1-\sum \limits_kp_k)$
$\quad 0 = \frac{\partial\mathcal{L}}{\partial p_k} = \frac{n_k}{p_k} - \lambda \quad 0 = \frac{\partial\mathcal{L}}{\partial \lambda} = 1 - \sum\limits_{k=1}^{d}p_k$
$p_k = \frac{n_k}{\sum_{k=1}^{d}n_k}$

• 카테고리 분포의 MLE는 경우의수를 세어서 비율을 구하는 것이다.

딥러닝에서 최대가능도 추정법

• 최대가능도 추정법을 이용해서 기계학습 모델을 학습할 수 있다.

$\widehat{\theta}_{MLE} = \argmax\limits_{\theta}\frac{1}{n}\sum \limits_{i=1}^{n}\sum \limits_{k=1}^{K}y_i,k \, log(MLP_{\theta}(x_i)_k)$

확률분포의 거리

• 기계학습에서 사용되는 손실함수들은 확률분포의 거리를 통해 유도된다.
• 데이터공간에 두 개의 확률분포 $P(x), Q(x)$가 있을 경우 두 확률분포 사이의 거리(distance)를 계산할 때 다음과 같은 함수들을 이용한다.
  • 총변동거리 (Total Variation Distance, TV)
  • 쿨백-라이블러 발산 (Kullback-Leibler Divergence, KL)
  • 바슈타인 거리 (Wasserstein Distance)

쿨백-라이블러 발산

• 쿨백-라이블러 발산(KL Divergence)은 다음과 같이 정의한다.

이산확률변수 $KL(P||Q) = \sum \limits_{x \in \chi}P(x)\, log(\frac{P(x)}{Q(x)})$
연속확률변수 $KL(P||Q) = \int_\chi P(x) \, log(\frac{P(x)}{Q(x)})dx$

• 쿨백 라이블러는 다음과 같이 분해할 수 있다.

$KL(P||Q) = -E_{x\sim P(x)}[log \, Q(x)]+E_{x\sim P(x)}[log \, P(x)]$
$\qquad \qquad \qquad \quad \small{\text{크로스 엔트로피}} \qquad \quad \small{\text{엔트로피}}$

• 분류 문제에서 정답레이블을 $P$, 모델 예측을 $Q$라 두면 최대가능도 추정법은 쿨백-라이블러 발산을 최소화하는 것과 같다.

8강: 베이즈 통계학

조건부 확률

• 베이즈 통계학을 이해하기 위해선 조건부확률의 개념을 이해해야 한다.

$P(A \cap B) = P(B)P(A|B)$

• 조건부확률 $P(A|B)$는 사건 $B$가 일어난 상황에서 사건 $A$가 발생할 확률을 의미한다.
• 베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법을 알려준다.

$P(B|A) = \frac{P(A \cap B)}{P(A)} = P(B) \frac{P(A|B)}{P(A)}$

$P(\theta|D) = P(\theta)\frac{P(D|\theta)}{P(D)}$

• $P(\theta|D)$는 사후확률(posterior), $P(\theta)$는 사전확률(prior), $P(D|\theta)$는 가능도(likelihood), $P(D)$는 Evidence이다.

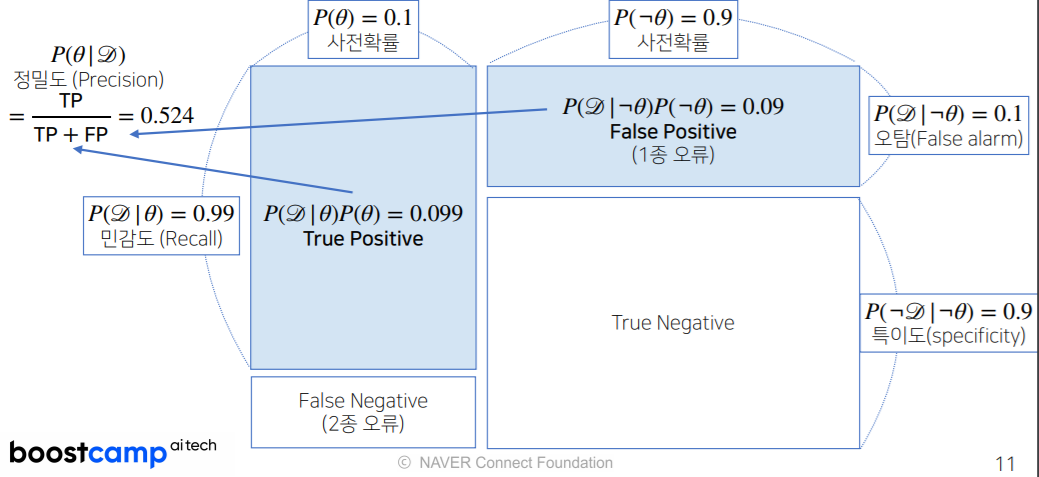
조건부 확률의 시각화

베이즈 정리를 통한 정보의 갱신

• 베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있다.
  

조건부 확률 -> 인과관계?

• 조건부 확률은 유용한 통계적 해석을 제공하지만 인과관계(causality)를 추론할 때 함부로 사용해서는 안 된다.
  • 데이터가 많아져도 조건부 확률만 가지고 인과관계를 추론하는 것은 불가능하다.
• 인과관계는 데이터 분포의 변화에 강건한 예측모형을 만들 때 필요하다.
  
• 인과관계를 알아내기 위해서는 중첩요인(confounding factor)의 효과를 제거하고 원인에 해당하는 변수만의 인과관계를 계산해야 한다.

10강: CNN

Convolution 연산

• Convolution 연산은 이와 달리 커널(kernel)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조이다.

$h_i = \sigma(\sum \limits_{j=1}^{k} V_j x_{i+j-1})$

• Convolution 연산의 수학적인 의미는 신호(signal)를 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링하는 것이다.

continuos(연속) $\quad [f *g](x) = \int_{R^d} f(z)g(x-z)dz = \int_{R^d} f(x-z)g(z)dz = [g*f](x)$

disrete(이산) $\quad [f *g](i) = \sum \limits_{a \in Z^d}f(a)g(i-a) = \sum \limits_{a \in Z^d}f(i-a)g(a) = [g*f](i)$

• CNN에서 사용하는 연산은 사실 convolution이 아니고 cross-correlation이다.

• 커널은 정의역 내에서 움직여도 변하지 않고(translation invariant) 주어진 신호에 국소적(local)으로 적용한다.

다양한 차원에서의 Convolution

1D-conv $\qquad[f*g](i) = \sum \limits_{p=1}^{d}f(p)g(i+p)$
2D-conv $\qquad[f*g](i, j) = \sum \limits_{p,q}f(p,q)g(i+p, j+q)$
3D-conv $\qquad[f*g](i, j, k) = \sum \limits_{p,q,r}f(p,q,r)g(i+p, j+q, k+r)$

• 데이터의 성격에 따라 사용하는 커널이 달라진다.
• $i, j, k$가 바뀌어도 커널의 값은 바뀌지 않는다.

2차원 Convolution 연산

다음은 2D-Conv 연산의 출력 크기이다.
입력 크기 = $(H, W)$, 커널 크기 = $(K_H, K_W)$, 출력 크기 = $(O_H, O_W)$
$O_H = H - K_H+1$
$O_W = W - K_W + 1$

• 채녈이 여러개인 2차원 입력의 경우 2차원 Convolution을 채널 개수만큼 적용한다고 생각하면 된다.

Convolution 연산의 역전파 이해하기

$\frac{\partial}{\partial x}[f*g](x) = \frac{\partial}{\partial x} \int_{R^d}f(y)g(x - y)dy$
$= \int_{R^d}f(y) \frac{\partial}{\partial x}(x-y)dy$
$= [f*g^\prime](x)$

• Descrete 일 때도 마찬가지로 성립한다.
• Convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나오게 된다.

3. 피어 세션 정리

• 7, 8, 9강 요약 정리
• 과제 1,2,3번 코드 리뷰
• 멘토링에 대한 토의

4. 과제 수행 과정

야구본다고 내일로 미룸.(선택 과제)

5. 회고

수식이 많아서 힘들었떤 하루였다. 그래도 덕분에 Latex실력이 조금 는거 같다. 내일은 꼭 파이썬 강의를 듣자. 모더레이터 처음이라서 제대로 했는지는 잘 모르겠다. 최대한 민폐 끼치지 않도록 노력하자.

6. 내일 할일

• 선택 과제
• AI 강의 하나밖에 없으니 내일부터 파이썬 강의 몰아서 듣자.